Update:
2019.7.15更新
万分感谢[宁信]大佬,认认真真地审核了本文章,指出了超过五处错误捂脸,太尴尬了.
万分感谢[宁信]大佬,认认真真地审核了本文章,指出了超过五处错误捂脸,太尴尬了.
万分感谢[宁信]大佬,认认真真地审核了本文章,指出了超过五处错误捂脸,太尴尬了.
重要事情说三遍!!!!!
2019.7.16更新
笔记再次完善,感谢[Ichinose]大佬提出的好问题,并且修改了代码部分的错误注释.
笔记再次完善,感谢[Ichinose]大佬提出的好问题,并且修改了代码部分的错误注释.
笔记再次完善,感谢[Ichinose]大佬提出的好问题,并且修改了代码部分的错误注释.
重要事情说三遍
2019.8.7更新
感谢QQ大佬,wust-pyoxiao大佬指出问题。
感谢QQ大佬,wust-pyoxiao大佬指出问题。
感谢QQ大佬,wust-pyoxiao大佬指出问题。
重要事情说三遍!!!!!
最近公共祖先
概念定义
对于节点(x,y)而言,如果说(z)节点既是(x)的祖先节点,也是(y)的祖先节点.
那么我们认为(z)节点是((x,y))的公共祖先节点.
公共祖先节点有很多,那么深度最大的节点,被称之为最近公共祖先.记为LCA(x,y)
你也可以认为(LCA(x,y))节点,是所有公共祖先节点中,离着(x,y)这两个点的距离最近.
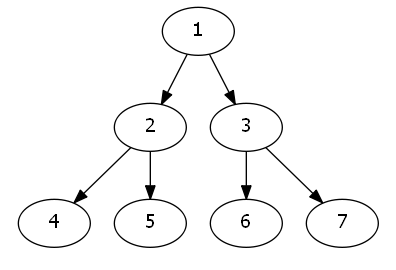
在这张图片上面,我们举几个例子.
树上倍增法
初始思维
树上倍增算法,是一个非常重要的算法,一般来说树上的问题,很多时候都会运用到树上倍增的算法思想.
我们知道,暴力算法,是一步,一步,一步非常踏实的算法.
但是我们知道,一步步走抵达终点太慢了,我们不得不学会连蹦带跳.
每一次都比上一次多跳一倍的格子.
我们发现,两个点的最近公共祖先,很多时候离他们很远.
换一张升级版本的图片
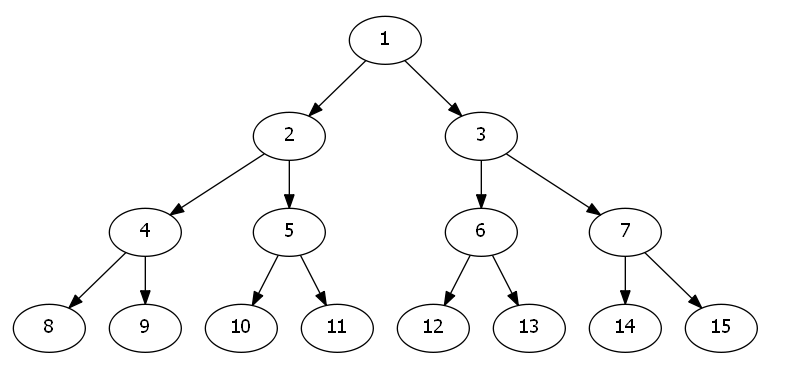
我们发现
他们的公共祖先离他们比较远.
我们可以分析一下.
这个式子的意思是.
也就是
假如说我们要用暴力方法的话.我们需要走三步,走一步要一格.
但是如果我们连蹦带跳的话.
第一跳,我们走一格.
第二跳,我们走两格.
我们惊奇地我们发现,我们只需要跳两次了.
倍增思想
既然如此的话,我们发现任意一个数字,都可以被划分成下面这个公式.
这就是我们的二进制划分的思想,任何一个数字都可以被二进制划分.
也可以这么理解,我们知道一个数有它的十进制表达,也有它的二进制表达.
我们所谓的划分,就是将一个十进制数,转换为二进制表达.
再举一个例子.
我们可以这么认为.
二进制表示下,计数位置从0开始.
之前有富有学习经验的大佬说代码部分.
for(int k=lg[deep[x]]-1; k>=0; k--) //从大到小,枚举我们所需要的长度.2^(log(deep[x]))~1
if(fa[x][k]!=fa[y][k])//如果发现x,y节点还没有上升到最近公共祖先节点
{
x=fa[x][k];//当然要跳跃
y=fa[y][k];//当然要跳跃
}
部分不利于初学者们理解.那么我们来认认真真地解析一下.
- 为什么要倒着循环,而且正着循环会出问题
我们来看一组样例.多么的250
我们将他们放到树上.也就是节点a离着最近公共祖先有(250)个距离.
假如说我们是顺着循环走的.我们必然走不到终点.
我们刚开始,走了(2^0)格,我们发现满足条件,于是我们走了(2^0)个格子.
我们然后,走了(2^1)格,我们发现也满足条件,((a,b))节点还是没有相遇,于是我们走了(2^1)个格子
我们接着,走(2^2)格子,我们惊奇地发现,也是满足条件的,于是我们走了(2^2)个格子.
不停地走啊走,我们永远都走不到终点.
因为抵达终点的路径,必须是二进制拆分下的路径.
接下来我们分析一下为什么我们最后一遍循环完后,不是是Lca节点,而且Lca节点的儿子节点.
if(fa[x][k]!=fa[y][k]) //如果不相遇
x=fa[x][k],y=fa[y][k];//我们才会跳跃.
那么我们实际能跳跃到的节点们,其实也就是a节点到Lca节点的儿子节点这一段上面的节点.
Lca节点,肯定fa[x][k]=fa[y][k].
但是我们fa[x][k]!=fa[y][k],所以Lca节点不能抵达.
但是Lca节点的儿子节点,肯定fa[x][k]!=fa[y][k].
所以Lca节点的儿子节点,是我们能够跳跃的最大距离了.
倍增数组
既然如此的话,我们不妨设置
我们知道二的幂次,是具有一个数学性质的.
或者你可以这么认为.
我们将这个数学性质,带入到我们的倍增数组,就会发现一个转移方程.
倍增数组就这么迅速地解决了!
算法流程
我们知道LCA(x,y)表示为两个节点的公共祖先.
也就是我们知道节点(x),和节点(y)总会在一个节点相遇.
也就是经过一系列跳跃过后的节点(x),和节点(y)的深度必须是相同的.
- 节点x必须和节点y在同一深度
根据这个条件,我们刚开始,显然深度更加深的节点(在下面的节点),跳跃到和另外一个节点(在上面的节点),一样的深度.
我们不妨认为,节点(x)深度更加深,是属于下面的节点.
如果x在上面,我们就交换x,y即可,反正要使得.
- 利用二进制划分,使得节点(x)向上调整到,和节点(y)的同一深度.
也就是不停地尝试让节点(x)往上走k步.
如果说我们发现,节点(x)往上走(k)步,还是在(y)下面.
- 如果说上调的过程中,发现(x=y),说明LCA找到了.
往上面看图片,你可以认为是节点2,和节点4的情况.节点2是节点4的父亲节点. - 当(x,y)节点他们的深度一致的时候,两个节点都向上跳跃同样高度,并且需要保证两个节点不相遇
为什么要跳跃同一高度?
之前我们就说了,两个节点必须保证同一高度.
为什么要保证两个节点不相遇,题目不是要我们找到最近公共祖先吗?
这是为了保证最近这个性质.
我们发现满足两个节点不相遇的,深度最浅的两个节点.也就是在最近公共祖先节点下面,离最近公共祖先节点,最近的节点.
就是最近公共祖先节点的两个儿子节点.
那么这两个儿子节点,他们的父亲节点,就必然是最近公共祖先节点.
怎么向上跳跃?其实和之前跳跃是一样的.
也就是不停地尝试让节点(x,y)往上走k步.
- 然后最后我们输出(F[x][0]),也就是x节点的父节点,我们的最近公共祖先.
代码解析
#include <bits/stdc++.h>
using namespace std;
int n,m,s,x,y,tot=0;
const int N=500005,M=1000005;//N存储节点总数,M存储边的总数
int head[N],edge[M],Next[M];
int deep[N],fa[N][22],lg[N];
//deep[i]是i号节点的深度
//lg是log数组
void add(int x,int y)//链式前项星加边
{
edge[++tot]=y;//存储节点
Next[tot]=head[x];//链表
head[x]=tot;//标记节点位置
return ;
}
void dfs(int x,int y)
{
deep[x]=deep[y]+1;//x是y的儿子节点,所以要+1
fa[x][0]=y;//fa[x][0]表示x的父亲节点,而y是x的父亲节点.
for(int i=1; (1<<i)<=deep[x]; i++) //2^i<=deep[x]表示不能跳出去了,最多跳到根节点上面
fa[x][i]=fa[fa[x][i-1]][i-1];//状态转移 2^i=2^(i-1)+2^(i-1)
for(int i=head[x]; i; i=Next[i]) //遍历所有的出边
if(edge[i]!=y)//因为是无向图,所以要避免回到父亲节点上面去了
dfs(edge[i],x);//访问儿子节点,并且标记自己是父亲节点
return ;//返回
}
int LCA(int x,int y)
{
if(deep[x]<deep[y])//强制要求x节点是在下方的节点
swap(x,y);//交换,维持性质
while(deep[x]>deep[y])//当我们还没有使得节点同样深度
x=fa[x][lg[deep[x]-deep[y]]-1];//往上面跳跃,deep[x]-deep[y]是高度差.-1是因为lg数组是Log值大1
if(x==y)//发现Lca(x,y)=y
return x;//返回吧,找到了...
for(int k=lg[deep[x]]-1; k>=0; k--) //从大到小,枚举我们所需要的长度.2^(log(deep[x]))~1
if(fa[x][k]!=fa[y][k])//如果发现x,y节点还没有上升到最近公共祖先节点
{
x=fa[x][k];//当然要跳跃
y=fa[y][k];//当然要跳跃
}
return fa[x][0];//必须返回x的父亲节点,也就是Lca(x,y)
}
int main()
{
scanf("%d%d%d",&n,&m,&s);//n个节点,m次询问,s为根节点
for(int i=1; i<n; i++) //n-1条边
{
scanf("%d%d",&x,&y);//读入边
add(x,y);//建立边
add(y,x);//建立无向图
}
dfs(s,0);//从根节点,开始建立节点之间的跳跃关系,根节点的父亲节点没有,故选择0
for(int i=1; i<=n; i++)
lg[i]=lg[i-1]+(1<<lg[i-1]==i);//处理log数组的关系,lg[x]=log(x)+1,请记得最后使用要-1
for(int i=1; i<=m; i++)
{
scanf("%d%d",&x,&y);//读入需要查询的节点
printf("%d
",LCA(x,y));//输出查询的结果
}
return 0;
}
例题
题目描述
Y岛风景美丽宜人,气候温和,物产丰富。
Y岛上有N个城市(编号(1,2,…,N)),有(N-1)条城市间的道路连接着它们。
每一条道路都连接某两个城市。
幸运的是,小可可通过这些道路可以走遍Y岛的所有城市。
神奇的是,乘车经过每条道路所需要的费用都是一样的。
小可可,小卡卡和小YY经常想聚会,每次聚会,他们都会选择一个城市,使得3个人到达这个城市的总费用最小。
由于他们计划中还会有很多次聚会,每次都选择一个地点是很烦人的事情,所以他们决定把这件事情交给你来完成。
他们会提供给你地图以及若干次聚会前他们所处的位置,希望你为他们的每一次聚会选择一个合适的地点。
输入格式
第一行两个正整数,(N)和(M),分别表示城市个数和聚会次数。
后面有(N-1)行,每行用两个正整数(A)和(B)表示编号为(A)和编号为(B)的城市之间有一条路。
再后面有(M)行,每行用三个正整数表示一次聚会的情况:小可可所在的城市编号,小卡卡所在的城市编号以及小YY所在的城市编号。
输出格式
一共有(M)行,每行两个数(Pos)和(Cost),用一个空格隔开,表示第(i)次聚会的地点选择在编号为(Pos)的城市,总共的费用是经过(Cost)条道路所花费的费用。
数据范围
输入样例:
6 4
1 2
2 3
2 4
4 5
5 6
4 5 6
6 3 1
2 4 4
6 6 6
输出样例:
5 2
2 5
4 1
6 0
解题报告
题意理解
不同于一般的LCA题目,这道题目是,在一棵(n-1)条边的树上,有三个节点,要你求出这个三个点抵达一个汇聚点的最少代价.
算法解析
这道题目的核心点,就是它是由三个点构成的最短路.
为什么,它同于一般的题目,难道不是让我们直接求出三个点的最近公共祖先?
汇聚点为什么不是
如果你真的是这么想,脑海里面只有A,B选项,那么你应该庆幸,出题人比较良心丧心病狂留下的唯一良知,他给你提出了一个样例,告诉你为什么不是这样.
因为文化课考试的时候,题目都是A,B,C或者再来一个D的单项选择题.
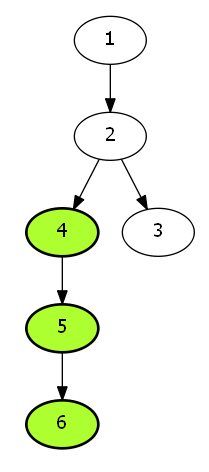
(3)人分别在(4,5,6)三个节点上面.
仔仔细细地观察一下,我们发现这道题目的汇聚点,应该是5,而不是4.
- 假如说我们按照楼上这个错误思路,我们的三点的最近公共祖先节点,应该是4.
- 但是最少花费,显然是在(5)号节点.
我们的思路居然是错误的!!!
它到底错误在了哪里.
我们要分析一下,这道题目,为什么选择的是5,而不是4?
选择(4),那么(1)号小朋友不需要行动.
选择(5),那么(2,3)号小朋友汇聚在点(5)后,都不需要行动.
我们可以这么现实化这道题目.
(2,3)号小朋友他们是互相的知己一对狗男女,所以说,他们想要先在一起.发朋友圈,秀恩爱
所以(2,3)号小朋友他们会先聚集在一起
花费代价为
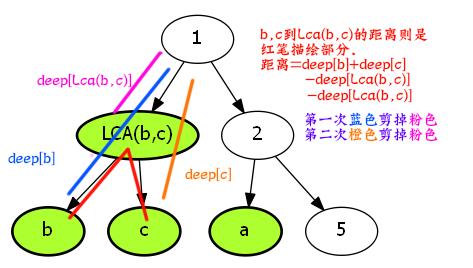
此时我们面临两大选择.
- (1)号同学孤身一人走到2,3号同学相遇的地方.
- (2,3)号同学一起
手拉手和(1)号同学相遇.再秀一次恩爱,虐一下单身狗1号
假如说(1)号同学,与(2,3)号同学相隔(L)个距离.
我们将会发现,两大选择,会产生两大代价.
然而显然一号选择是最好不过的了.
同样的距离,一个人是一个人走,一个是两个人走,那么必然一个人走消耗卡路里更少.
那么2,3号汇聚的话,他们会花费
之后一号过来找他们,距离消耗了:
这时候一号到了((x,y,z))公共祖先,然后一号朝(Lca(y,z))走
那么消耗总值就是
- (1,2)先在一起
- (2,3)先在一起
- (1,3)先在一起
代码解析
#include <bits/stdc++.h>
using namespace std;
const int N=500000+200,M=500000*2+100;
int n,m,s,lg[N],deep[N];
struct Lca
{
int head[M],Next[M],edge[M],tot,fa[N][22];
void init()
{
memset(head,0,sizeof(head));
tot=0;
}
void add_edge(int a,int b)
{
edge[++tot]=b;
Next[tot]=head[a];
head[a]=tot;
return ;
}
void dfs(int x,int y)
{
deep[x]=deep[y]+1;
fa[x][0]=y;
for(int i=1; (1<<i)<=deep[x]; i++)
fa[x][i]=fa[fa[x][i-1]][i-1];
for(int i=head[x]; i; i=Next[i])
if (edge[i]!=y)
dfs(edge[i],x);
return ;
}
int LCA(int x,int y)
{
if (deep[x]<deep[y])
swap(x,y);
while(deep[x]>deep[y])
x=fa[x][lg[deep[x]-deep[y]]-1];
if (x==y)
return x;
for(int k=lg[deep[x]]-1; k>=0; k--)
if (fa[x][k]!=fa[y][k])
{
x=fa[x][k];
y=fa[y][k];
}
return fa[x][0];
}
} g1;
int main()
{
scanf("%d%d",&n,&m);
g1.init();
for(int i=1; i<n; i++)
{
int a,b;
scanf("%d%d",&a,&b);
g1.add_edge(a,b);
g1.add_edge(b,a);
}
g1.dfs(1,0);
for(int i=1; i<=n; i++)
lg[i]=lg[i-1]+(1<<lg[i-1]==i);
for(int i=1; i<=m; i++)
{
int x,y,z,c_x,c_y,c_z,dx,dy,dz;
scanf("%d%d%d",&x,&y,&z);
c_x=g1.LCA(x,y),dx=deep[x]+deep[y]-deep[c_x]+deep[z]-2*deep[g1.LCA(z,c_x)];
c_y=g1.LCA(y,z),dy=deep[y]+deep[z]-deep[c_y]+deep[x]-2*deep[g1.LCA(x,c_y)];
c_z=g1.LCA(x,z),dz=deep[x]+deep[z]-deep[c_z]+deep[y]-2*deep[g1.LCA(y,c_z)];
if(dx>dy)
dx=dy,c_x=c_y;
if(dx>dz)
dx=dz,c_x=c_z;
printf("%d %d
",c_x,dx);
}
return 0;
}