【剑指Offer】42、和为S的两个数字

  题目描述：

  输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。

  输出描述：

  对应每个测试案例，输出两个数，小的先输出。

  解题思路：

  对于本题，比上一题简单一些。看到题目，我们的第一感觉是暴力解法，即先在数组中固定一个数字，然后依次判断数组中其他数字与它的和是不是等于S。这显然复杂度为O(n^2)。

  进一步分析，类似于上一题的思路，我们可以使用双指针解法。我们定义两个指针low和high，low从左向右遍历，high从右向左遍历，也就是low指向第一个元素，high指向最后一个元素。首先，比较low和high的和与给定的S，如果和小于S，那么就要增大输入值，即low向右移动一位；如果和大于S，那么就要减小输入值，即high向左移动一位；如果和等于S，那么这两个数字就是我们要找的数字。依次循环查找，直到low和high相等为止。

  这个算法只需要最多一次扫描，复杂度为O(n)，并且还有一个好处，就是这样找到的两个数满足乘积最小的条件。这可以这样证明：考虑x+y=C（C是常数），xy的大小。不妨设y>=x，y-x=d>=0，即y=x+d, 2x+d=C, x=(C-d)/2, xy=x(x+d)=(C-d)(C+d)/4=(C^2-d^2)/4，也就是xy是一个关于变量d的二次函数，对称轴是y轴，开口向下。d是>=0的，d越大, xy也就越小。

  举例：

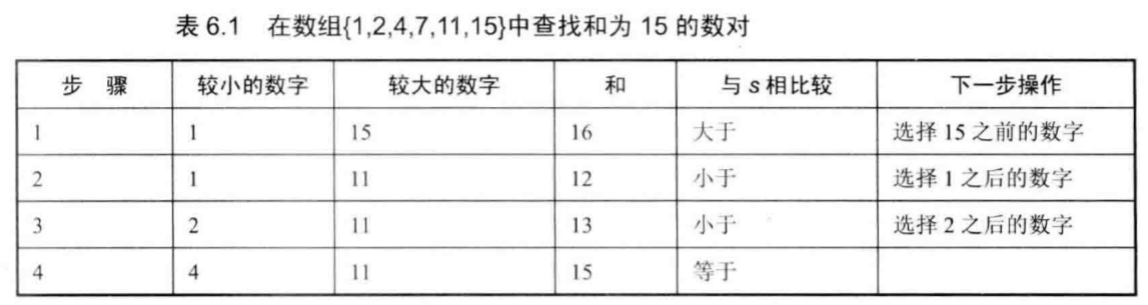
  编程实现（Java）：

import java.util.ArrayList;
public class Solution {
    public ArrayList<Integer> FindNumbersWithSum(int [] array,int sum) {
        ArrayList<Integer> res=new ArrayList<>();
        int low=0,high=array.length-1;
        while(low<high){
            int curSum=array[low]+array[high];
            if(curSum==sum){ //找到一个解
                res.add(array[low]);
                res.add(array[high]);
                break;
            }
            else if(curSum<sum)
                low++;
            else
                high--;
        }
        return res;
    }
}