Given a string s, partition s such that every substring of the partition is a palindrome.
Return the minimum cuts needed for a palindrome partitioning of s.
Example:
Input: "aab" Output: 1 Explanation: The palindrome partitioning ["aa","b"] could be produced using 1 cut.
Approach #1: DP. [C++]
class Solution {
public:
int minCut(string s) {
int len = s.length();
if (len == 0) return 0;
vector<vector<bool>> isPanlindrome(len+1, vector<bool>(len+1, false));
vector<int> cuts(len);
for (int i = 0; i < len; ++i) {
int minn = i;
for (int j = 0; j <= i; ++j) {
if (s[j] == s[i] && (i-j < 2 || isPanlindrome[j+1][i-1])) {
isPanlindrome[j][i] = true;
minn = j == 0 ? 0 : min(minn, cuts[j-1] + 1);
}
}
cuts[i] = minn;
}
return cuts[len-1];
}
};
Analysis:
isPalindrome[i][j] represent the characters from i to j is palindrome.
cuts[i] represent the index from 0 to i need to cut how many time so that it can be satify the condition.
2021-04-16
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文。
返回符合要求的 最少分割次数 。
示例 1:
输入:s = "aab"
输出:1
解释:只需一次分割就可将 s 分割成 ["aa","b"] 这样两个回文子串。
示例 2:
输入:s = "a"
输出:0
示例 3:
输入:s = "ab"
输出:1
提示:
1 <= s.length <= 2000
s 仅由小写英文字母组成
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/palindrome-partitioning-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题意:
这是一道经典的DP题,可以采用二维DP(本题会超时),也可以进一步优化从而使DP降到一维。因为二维DP相对容易理解些,所以我们先从二维DP来计算。
题解:
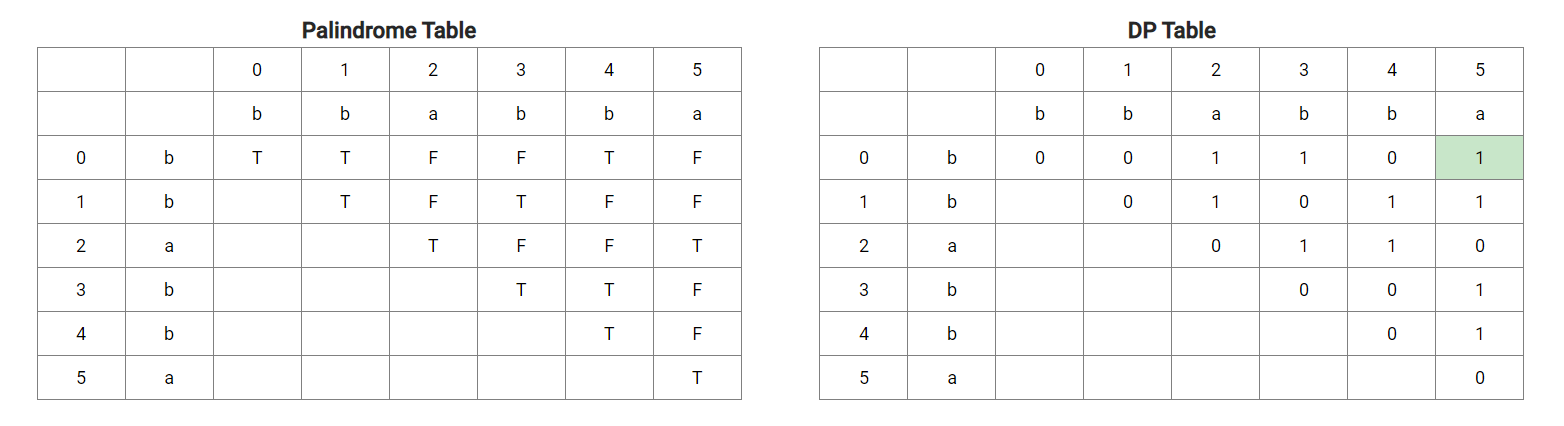
palindromeTable[i][j]:用来表示s[i][j]是否是一个回文字符串,它有三种状态:
- length = 1时:
- palindromeTable[i][i] = true
- length = 2时:
- if s[i] == s[i+1]: palindromeTable[i][j] = true
- else: palindromeTable[i][j] = false
- length > 2时:
- if s[i] == s[j]: palindromeTable[i][j] = palindromeTable[i-1][j-1]
- else: palindromeTable[i][j] = false
dpTable[i][j]:用来表示将s[i][j]拆分成都是回文的子串所需要的最少拆分次数,它也是有三种状态:
- length = 1时:
- dpTable[i][i] = 0
- length = 2时:
- if s[i] == s[i+1]: dpTable[i][i+1] = 0
- else: dpTable[i][i+1] = 1
- length > 2时:
- if palindromeTable[i][j] = true: dpTable[i][j] = 0
- else: dpTable[i][j] = min(dpTable[i][j], dpTable[i][k] + dpTable[k+1][j] + 1),其中i < k < j
最后的结果就是DPTable[0][len-1]。
代码:
#include <iostream> #include <string> #include <vector> using namespace std; const int inf = 0x7fffffff; void creatPalindromeTable(const string& s, vector<vector<bool> >& table) { int len = s.length(); // length = 1 for (int i = 0; i < len; ++i) table[i][i] = true; // length = 2 for (int i = 0; i < len - 1; ++i) if (s[i] == s[i + 1]) table[i][i + 1] = true; // length > 2 for (int i = 3; i <= len; ++i) { for (int j = 0; j + i <= len; ++j) { if (s[j] == s[j + i - 1]) { table[j][j + i - 1] = table[j + 1][j + i - 2]; } } } } void creatDpTable(const string& s, vector<vector<int> >& dpTable) { int len = s.length(); vector<vector<bool> > palindromeTable(len, vector<bool>(len, false)); creatPalindromeTable(s, palindromeTable); // length = 1 for (int i = 0; i < len; ++i) dpTable[i][i] = 0; // length = 2 for (int i = 0; i < len - 1; ++i) if (s[i] == s[i + 1]) dpTable[i][i + 1] = 0; else dpTable[i][i + 1] = 1; // length > 2 for (int i = 3; i <= len; ++i) { for (int j = 0; j + i <= len; ++j) { if (palindromeTable[j][j + i - 1]) dpTable[j][j + i - 1] = 0; else for (int k = j; k < j + i - 1; ++k) dpTable[j][j + i - 1] = min(dpTable[j][j + i - 1], dpTable[j][k] + dpTable[k + 1][j + i - 1] + 1); } } } int main() { string s; cin >> s; int len = s.length(); vector<vector<int> > dpTable(len, vector<int>(len, inf)); creatDpTable(s, dpTable); cout << dpTable[0][len - 1] << endl; return 0; }
这样做提交的时候会报超时,因为这道题的最后结果只需要dpTable就可以了,所以我们可以想办法对dpTable进行降维,使dpTable默认从0开始dpTable[i]即表示dpTable[0][i]。这样的话就可以把时间复杂度从O(n^3)降到O(n^2)。
dpTable[i]:代表从0到i所需的最小分割次数,共有两种状态。
- if palindromeTable[0][i] = true: dpTable[i] = 0
- else : dpTable[i] = min(dpTable[i], dpTable[j]+1), 其中 0 < j < i。
代码:
#include <iostream> #include <string> #include <vector> using namespace std; const int inf = 0x7fffffff; void creatPalindromeTable(const string& s, vector<vector<bool> >& table) { int len = s.length(); // length = 1 for (int i = 0; i < len; ++i) table[i][i] = true; // length = 2 for (int i = 0; i < len - 1; ++i) if (s[i] == s[i + 1]) table[i][i + 1] = true; // length > 2 for (int i = 3; i <= len; ++i) { for (int j = 0; j + i <= len; ++j) { if (s[j] == s[j + i - 1]) { table[j][j + i - 1] = table[j + 1][j + i - 2]; } } } } void creatDpTable(const string& s, vector<int>& dpTable) { int len = s.length(); vector<vector<bool> > palindromeTable(len, vector<bool>(len, false)); creatPalindromeTable(s, palindromeTable); for (int i = 0; i < len; ++i) { if (palindromeTable[0][i]) dpTable[i] = 0; else { for (int j = 0; j < i; ++j) { if (palindromeTable[j + 1][i]) dpTable[i] = min(dpTable[i], dpTable[j] + 1); } } } } int main() { string s; cin >> s; int len = s.length(); vector<int> dpTable(len, inf); creatDpTable(s, dpTable); cout << dpTable[len - 1] << endl; return 0; }