918. Maximum Sum Circular Subarray

Given a circular array C of integers represented by A, find the maximum possible sum of a non-empty subarray of C.

Here, a circular array means the end of the array connects to the beginning of the array.  (Formally, C[i] = A[i] when 0 <= i < A.length, and C[i+A.length] = C[i] when i >= 0.)

Also, a subarray may only include each element of the fixed buffer A at most once.  (Formally, for a subarray C[i], C[i+1], ..., C[j], there does not exist i <= k1, k2 <= j with k1 % A.length = k2 % A.length.)

Example 1:

Input: [1,-2,3,-2]
Output: 3
Explanation: Subarray [3] has maximum sum 3

Example 2:

Input: [5,-3,5]
Output: 10
Explanation: Subarray [5,5] has maximum sum 5 + 5 = 10

Example 3:

Input: [3,-1,2,-1]
Output: 4
Explanation: Subarray [2,-1,3] has maximum sum 2 + (-1) + 3 = 4

Example 4:

Input: [3,-2,2,-3]
Output: 3
Explanation: Subarray [3] and [3,-2,2] both have maximum sum 3

Example 5:

Input: [-2,-3,-1]
Output: -1
Explanation: Subarray [-1] has maximum sum -1

Note:

1. -30000 <= A[i] <= 30000
2. 1 <= A.length <= 30000

Approach #1: Array. [Java]

class Solution {
    public int maxSubarraySumCircular(int[] A) {
        int curMax = 0, sumMax = -30000, 
            curMin = 0, sumMin = 30000, total = 0;
        for (int i = 0; i < A.length; ++i) {
            curMax = Math.max(curMax + A[i], A[i]);
            sumMax = Math.max(sumMax, curMax);
            curMin = Math.min(curMin + A[i], A[i]);
            sumMin = Math.min(curMin, sumMin);
            total += A[i];
        }
        return sumMax > 0 ? Math.max(sumMax, total - sumMin) : sumMax;
    }
}

　　

Analysis:

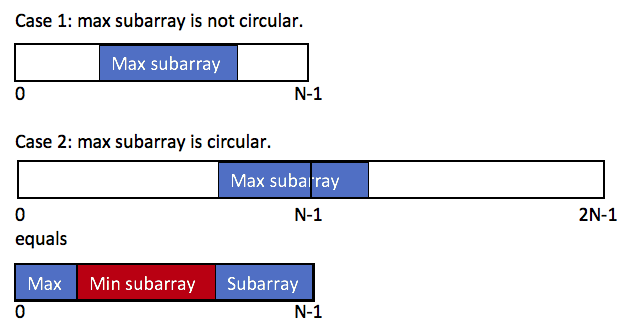
There are two case.

The first is that the subarray take only a middle part, and we know how to find the max subarray sum.

The second is that the subarray take a part of head array and a part of tail array.

We can transfer this case to the first one.

The maximum result equals to the total sum minus the minimum subarray sum.

Here is a diagram by @mototix:

So the max subarray cricular sum equals to 

max(the max subarray sum, the total sum - the min subarray sum)

Corner case:

Just one to pay attention:

If all number are negative, maxSum = max(A) and minSum = sum(A). In this case, max(maxSum, total - minSum) = 0, which means the sum of an empty subarray. According to the deacription, We need to return the max(A), instead of sum of an empty subarray. So we return the maxSum to handle this corner case.

Complexity:

One pass, time O(N).

No extra space, space O(1)

Reference:

https://leetcode.com/problems/maximum-sum-circular-subarray/discuss/178422/One-Pass