1127 ZigZagging on a Tree

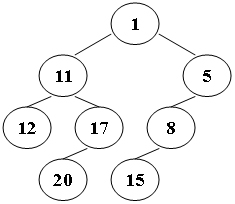
Suppose that all the keys in a binary tree are distinct positive integers. A unique binary tree can be determined by a given pair of postorder and inorder traversal sequences. And it is a simple standard routine to print the numbers in level-order. However, if you think the problem is too simple, then you are too naive. This time you are supposed to print the numbers in "zigzagging order" -- that is, starting from the root, print the numbers level-by-level, alternating between left to right and right to left. For example, for the following tree you must output: 1 11 5 8 17 12 20 15.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the inorder sequence and the third line gives the postorder sequence. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the zigzagging sequence of the tree in a line. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

8
12 11 20 17 1 15 8 5
12 20 17 11 15 8 5 1

 

Sample Output:

1 11 5 8 17 12 20 15

题意：

　　给出中序和后序遍历的结果，要求按照从右到左，从左到右依次替换的方法来输出层次遍历的结果。（Too native.）

思路：

　　构造数，层次遍历，遍历的过程中用双向队列来存储每一层的数据，没遍历完一层，根据要求判断所在层数是pop_front()还是pop_back()。

Code：

#include <bits/stdc++.h>

using namespace std;

vector<int> inOrder(50);
vector<int> postOrder(50);

typedef struct Node* node;

struct Node {
    int date;
    node left;
    node right;
    Node(int v) {
        date = v;
        left = NULL;
        right = NULL;
    }
};

node buildTree(int index, int left, int right) {
    if (left > right) return NULL;
    node root = new Node(postOrder[index]);
    int pos;
    for (int i = left; i <= right; ++i) {
        if (inOrder[i] == postOrder[index]) {
            pos = i;
            break;
        }
    }
    int len = right - pos;
    root->left = buildTree(index - len - 1, left, pos - 1);
    root->right = buildTree(index - 1, pos + 1, right);
    return root;
}

void levelOrder(node root) {
    queue<node> que;
    deque<int> level;
    vector<int> ans;
    node last = new Node(-1);
    que.push(root);
    que.push(last);
    bool leftToRight = false;
    while (!que.empty()) {
        node temp = que.front();
        que.pop();
        if (temp->date == -1) {
            if (que.empty() && level.empty()) break;
            que.push(last);
            if (leftToRight) {
                while (!level.empty()) {
                    ans.push_back(level.front());
                    level.pop_front();
                }
                leftToRight = false;
            } else {
                while (!level.empty()) {
                    ans.push_back(level.back());
                    level.pop_back();
                }
                leftToRight = true;
            }
        } else {
            level.push_back(temp->date);
            if (temp->left) que.push(temp->left);
            if (temp->right) que.push(temp->right);
        }
    }
    cout << ans[0];
    for (int i = 1; i < ans.size(); ++i) cout << " " << ans[i];
    cout << endl;
}

int main() {
    int n;
    cin >> n;

    for (int i = 0; i < n; ++i) cin >> inOrder[i];
    for (int i = 0; i < n; ++i) cin >> postOrder[i];

    node root = buildTree(n - 1, 0, n - 1);

    levelOrder(root);

    return 0;
}

---

　　多看看别人的博客，看一下同一道问题的不同解，也能够让自己的思维更加的开阔。

　　我写的代码还是按照中规中矩的方法来解决问题，看了柳神的博客感觉它的代码更加的简练，也更加的值得我去学习。

Code：

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
vector<int> in, post, result[35];
int n, tree[35][2], root;
struct node {
    int index, depth;
};
void dfs(int &index, int inLeft, int inRight, int postLeft, int postRight) {
    if (inLeft > inRight) return;
    index = postRight;
    int i = 0;
    while (in[i] != post[postRight]) i++;
    dfs(tree[index][0], inLeft, i - 1, postLeft, postLeft + (i - inLeft) - 1);
    dfs(tree[index][1], i + 1, inRight, postLeft + (i - inLeft), postRight - 1);
}
void bfs() {
    queue<node> q;
    q.push(node{root, 0});
    while (!q.empty()) {
        node temp = q.front();
        q.pop();
        result[temp.depth].push_back(post[temp.index]);
        if (tree[temp.index][0] != 0)
            q.push(node{tree[temp.index][0], temp.depth + 1});
        if (tree[temp.index][1] != 0)
            q.push(node{tree[temp.index][1], temp.depth + 1});
    }
}
int main() {
    cin >> n;
    in.resize(n + 1), post.resize(n + 1);
    for (int i = 1; i <= n; i++) cin >> in[i];
    for (int i = 1; i <= n; i++) cin >> post[i];
    dfs(root, 1, n, 1, n);
    bfs();
    printf("%d", result[0][0]);
    for (int i = 1; i < 35; i++) {
        if (i % 2 == 1) {
            for (int j = 0; j < result[i].size(); j++)
                printf(" %d", result[i][j]);
        } else {
            for (int j = result[i].size() - 1; j >= 0; j--)
                printf(" %d", result[i][j]);
        }
    }
    return 0;
}

2020-07-07 21:29:02