Solved
- Problem B: Battle Royale
- Problem C: Coolest Ski Route
- Problem D: Down the Pyramid
- Problem E: Expired License
- Problem F: Fighting Monsters
- Problem H: Hyper Illuminati
- Problem I: It’s Time for a Montage
- Problem K: Kitchen Cable Chaos
- Problem L: Logic Puzzle
- Problem M: Mountaineers
Solutions
Problem B: Battle Royale
题意:
给出一个大圆和小圆,保证小圆在大圆内,给出两个在大圆内的点,保证这两个点的连线和小圆相交,问从一点走到另一点最短距离是多少(路径不能在小圆内)。
想法:
最短路径一定是两个点和圆的两条切线和一部分圆弧。
如图:
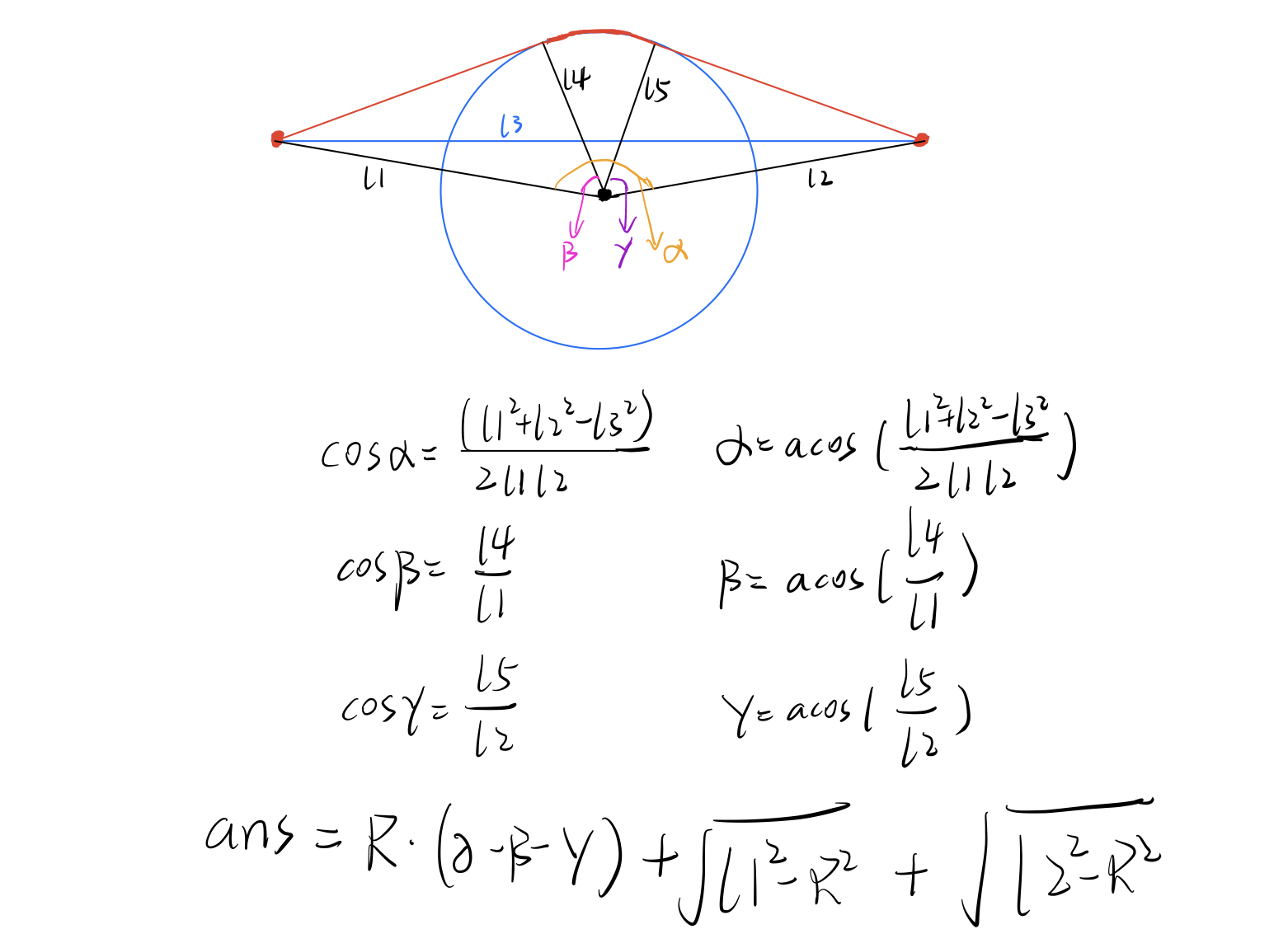
代码:
double x_1,y_1,x_2,y_2;
double xr,yr,r;
double dis(double x,double y,double xx,double yy)
{
return sqrt((xx-x)*(xx-x)+(yy-y)*(yy-y));
}
int main()
{
scanf("%lf%lf%lf%lf",&x_1,&y_1,&x_2,&y_2);
scanf("%lf%lf%lf",&xr,&yr,&r);
scanf("%lf%lf%lf",&xr,&yr,&r);
double l1,l2,l3;
l1=dis(x_1,y_1,xr,yr);
l2=dis(x_2,y_2,xr,yr);
l3=dis(x_1,y_1,x_2,y_2);
double a,b,c;
a=acos((l1*l1+l2*l2-l3*l3)/(2*l1*l2));
b=acos(r/l1);
c=acos(r/l2);
double ans;
ans=r*(a-b-c)+sqrt(l1*l1-r*r)+sqrt(l2*l2-r*r);
printf("%.10f",ans);
}
Problem C: Coolest Ski Route
题意:
求一幅 (DAG) 上的最长路,每个点只能经过一次。
想法:
用 (dis[i]) 表示从 (i) 点开始的最长路,对每个点 (dfs) ,在 (dfs) 去维护最大值,但保证每个点只经过一次即可。
代码:
vector<int>v[1010];
int mp[1010][1010];
int dist[1010];
bool vis[1010];
int n,m;
int dfs(int step)
{
if(vis[step]) return dist[step];
for(int i=0;i<v[step].size();i++)
{
dist[step]=max(dist[step],dfs(v[step][i])+mp[step][v[step][i]]);
}
vis[step] = 1;
return dist[step];
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int s,t,c;
cin>>s>>t>>c;
v[s].push_back(t);
mp[s][t] = max(mp[s][t],c);
}
int maxx = 0;
for(int i=1;i<=n;i++)
{
maxx = max(maxx,dfs(i));
}
cout<<maxx<<endl;
}
Problem D: Down the Pyramid
题意:
给你数字金字塔的第二层,让你求第一层有多少种可能性。
想法:
设第一层的 (b[1]=x) ,那么可以推出:
(b[2]=a[1]-b[1])
(b[3]=a[2]-b[2])
(b[4]=a[3]-b[3])
(......)
(b[n+1]=a[n]-b[n])
存在条件 (0 leqslant b[i]),即可去推出数量。
代码:
ll a[1001000];
ll b[1000100];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
b[1] = 0;
int ans = 2;
for(int i=1;i<=n;i++)
{
b[ans] = a[i] - b[ans-1];
ans++;
}
/*for(int i=1;i<ans;i++)
{
cout<<b[i]<<" ";
}
cout<<endl;*/
ll minn = 0;
for(int i=1;i<ans;i+=2)
{
if(b[i]<0)
{
minn = min(minn,b[i]);
}
}
minn = -minn;
ll maxx = 10000000000;
for(int i=2;i<ans;i+=2)
{
if(b[i]-minn<0)
{
puts("0");
return 0;
}
else{
maxx = min(maxx,b[i]-minn+1);
}
}
cout<<maxx<<endl;
}
Problem E: Expired License
题意:
给你 (a,b) 两个实数 ((0<=a,b<=100)),问能否找到两个数 (p,q) ,使得 (frac{a}{b} =frac{p}{q}),且 (p,q) 为素数。 (a,b) 保证小数点后位数不超过5位。
想法:
- 把 (a,b) 分别乘 (10^5),这样 (a,b) 都变成了整数。
- 然后求 (gcd(a,b)),如果 (frac{a}{gcd(a,b)}) 和
(frac{b}{gcd(a,b)}) 都为素数那么输出 (frac{a}{gcd(a,b)}, frac{b}{gcd(a,b)}),否则输出 (impossible),注意如果 (a==b),则输出 (2,2)。
代码:
const int maxn = 1e7+5;
int prime[maxn];
int visit[maxn];
void Prime(){
mem(visit,0);
mem(prime, 0);
for (int i = 2;i <= maxn; i++) {
//cout<<" i = "<<i<<endl;
if (!visit[i]) {
prime[++prime[0]] = i; //纪录素数, 这个prime[0] 相当于 cnt,用来计数
}
for (int j = 1; j <=prime[0] && i*prime[j] <= maxn; j++) {
// cout<<" j = "<<j<<" prime["<<j<<"]"<<" = "<<prime[j]<<" i*prime[j] = "<<i*prime[j]<<endl;
visit[i*prime[j]] = 1;
if (i % prime[j] == 0) {
break;
}
}
}
}
ll change(string s)
{
int len = s.length();
int k = len;
ll xx = 0;
for(int i=0;i<len;i++)
{
if(s[i]=='.')
{
k=i;
break;
}
xx=xx*10+s[i]-'0';
}
ll yy = 0;
int ans = 10000;
for(int i=k+1;i<len;i++)
{
yy +=(s[i]-'0')*ans;
ans/=10;
}
return xx*100000+yy;
}
int main()
{
int T;
Prime();
cin>>T;
while(T--)
{
string a,b;
cin>>a>>b;
ll x = change(a);
ll y = change(b);
//cout<<x<<" "<<y<<endl;
ll ans = __gcd(x,y);
ll c = x/ans;
ll d = y/ans;
if(c==d){
cout<<2<<" "<<2<<endl;
continue;
}
if(visit[c]==0&&visit[d]==0&&c!=1&&d!=1)
{
cout<<c<<" "<<d<<endl;
}
else{
puts("impossible");
}
}
}
Problem F: Fighting Monsters
题意:
给你 (n) 个怪兽的血量, (n) 个怪兽的当前血量就是它们的攻击力,两个怪兽之间对战规则是由血量少的一方先攻击,然后交替攻击,直到某一方的血量小于等于 (0) ,问是否存在一对怪兽在一方怪兽死亡后,另一方的血量为 (1)。
想法:
模拟两个怪兽相互进攻的过程,发现符合条件的怪兽一定是斐波那契数列中相邻的两个数字。
代码:
ll a[1001000];
ll b[1000100];
map<int,int>mp;
map<int,int>mm;
map<int,int>mo;
int f[1000100];
int main()
{
int n;
cin>>n;
int ans = 0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
mo[a[i]] = i;
if(a[i]==1) ans++;
b[i] = a[i];
}
//sort(a+1,a+1+n);
if(ans>=2)
{
int q = 0;
for(int i=1;i<=n;i++)
{
if(a[i]==1)
{
cout<<i<<" ";
q++;
}
if(q>=2) break;
}
return 0;
}
bool flag = 0;
f[1] = 1;
f[0] = 1;
mp[1] = 1;
mm[1] = 0;
for(int i=2;i<10000;i++)
{
f[i] = f[i-1] + f[i-2];
mp[f[i]] = 1;
mm[f[i]] = f[i-1];
if(f[i]>1000000)
{
break;
}
}
for(int i=1;i<=n;i++)
{
if(mp[a[i]]&&mo[mm[a[i]]])
{
//cout<<mm[a[i]]<<endl;
if(a[i]<a[mo[mm[a[i]]]])
cout<<i<<" "<<mo[mm[a[i]]]<<endl;
else{
cout<<mo[mm[a[i]]]<<" "<<i<<endl;
}
flag = 1;
break;
}
}
if(!flag) puts("impossible");
}
Problem H: Hyper Illuminati
题意:
给你 (m),问是否存在 (s,n) 满足 (sum^{s}_{p=1} p^{n-1}=m)
想法:
(n>=3) ,那么 (n) 的范围一定很小,(s) 由于是指数增长同样枚举次数也很少,因此可以直接暴力。
代码:
ll qpow(ll a,ll b)
{
ll ans=1;
while(b){
if(b%2==1){
ans=ans*a;
}
a=a*a;
b/=2;
}
return ans;
}
int main()
{
ll m;
ll n,k;
//cout<<qpow(2,5)<<endl;
cin>>m;
ll sum=0;
for(int i=3;i<=60;i++){
sum=0;
for(int j=1;j<=sqrt(m);j++){
sum+=qpow(j,i-1);
if(sum==m){
cout<<i<<" "<<j<<endl;
return 0;
}
if(sum>m)break;
}
}
printf("impossible");
}
Problem I: It’s Time for a Montage
题意:
(n) 个怪兽和英雄,第 (i) 个怪兽对战 第 (i) 个英雄,对战规则是按顺序一一对决,如果某一方大于另一方直接获胜,如果最终没有决出胜负,则英雄获胜。你可以通过对某个英雄训练,训练一天增加一点能力,问最小需要训练几天才能获胜。
想法:
(n) 很小,直接枚举在第 (i) 天获胜时所需要训练天数,然后取最小值。
代码:
int h[1005],v[1005];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
scanf("%d",&h[i]);
}
for(int i=1;i<=n;i++){
scanf("%d",&v[i]);
}
int ans=2005;
int num=0;
for(int i=0;i<=1000;i++){
int k=0;
for(int j=1;j<=n;j++){
if(j<n){
if(h[j]+i>v[j]){
k=1;
break;
}else if(h[j]+i<v[j]){
break;
}
}else{
if(h[j]+i>=v[j]){
k=1;
break;
}else if(h[j]+i<v[j]){
break;
}
}
}
if(k){
printf("%d
",i);
return 0;
}
}
}
Problem K: Kitchen Cable Chaos
题意:
两个器械之间距离为 (g) ,器械上也有长度为 (5) 的接触线,有 (n) 根电线长度分别为 (d[i]) ,每个电线左右两端都有长度为 (5) 的接触线,这部分线可以和另一根电线的接触线相重合。设所有相重合的长度中最短长度为这段线缆的质量,问这段线缆最大的质量是多少。
想法:
- 题目也就转化为选几段线缆,设这几个线缆长度为 (sum^{}_{} d),那么接触部分总长度为 (sum^{}_{} d+10-g),要让最小值最大,显然均分,答案就是 ((sum^{}_{} d+10-g)/(i+1))。
- 用背包去求 (sum^{}_{}d), (dp[i][j]) 表示选择i条线段时长度为j是否可能。然后求出答案即可。
代码:
const int maxn=10010;
int dp[61][maxn],a[maxn];
int main()
{
int n,g;
cin>>n>>g;
mem(dp,0);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
dp[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=n;j>=1;j--){
for(int k=maxn-1;k>=a[i];k--){
dp[j][k]+=dp[j-1][k-a[i]];
}
}
}
double maxx=-1.0;
for(int k=g-10;k<=maxn-1;k++){
for(int j=1;j<=n;j++){
//cout<<dp[j][k]<<endl;
if(!dp[j][k])continue;
double temp=1.0*(k+10-g)/(j+1.0);
if(temp<=5){
maxx=max(temp,maxx);
}
}
}
if(maxx<0){
printf("impossible");
}else{
printf("%.8lf
",maxx);
}
}
Problem L: Logic Puzzle
题意:
给你扫雷后的图,让你复原原图。
想法:
每个点遍历即可。
代码:
int n,m;
int mp[505][505];
int c[505][505];
bool check(int a,int b)
{
int ans=1;
for(int x=max(0,a-1);x<=min(a+1,n+1);x++){
for(int y=max(0,b-1);y<=min(b+1,m+1);y++){
ans*=c[x][y];
}
}
return (ans!=0);
}
void change(int a,int b)
{
for(int x=max(0,a-1);x<=min(a+1,n+1);x++){
for(int y=max(0,b-1);y<=min(b+1,m+1);y++){
c[x][y]--;
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<n+2;i++){
for(int j=0;j<m+2;j++){
scanf("%d",&c[i][j]);
//cout<<"x";
}
}
//cout<<"xx";
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(check(i,j)){
mp[i][j]=1;
change(i,j);
}
}
}
for(int i=1;i<=m;i++){
if(check(0,i))change(0,i);
if(check(0,n))change(0,n);
}
for(int i=1;i<=n;i++){
if(check(i,0))change(i,0);
if(check(i,m))change(i,m);
}
if(check(0,0))change(0,0);
if(check(0,m+1))change(0,m+1);
if(check(n+1,0))change(n+1,0);
if(check(n+1,m+1))change(n+1,m+1);
for(int i=0;i<=n+1;i++){
for(int j=0;j<=m+1;j++){
if(c[i][j]!=0){
printf("impossible");
return 0;
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(mp[i][j]){
printf("X");
}else{
printf(".");
}
}
cout<<endl;
}
return 0;
}
Problem M: Mountaineers
题意:
(n imes m) 的方格内,每个格子都有高度为 (h[i][j]) 的一座山,给出 (q) 次询问,问从 ((x1,y1)) 到 ((x2,y2)) 需要翻过的山的最大值的最小值是多少。
想法:
- 考虑用并查集去维护两座山之间能否到达。
- 考虑两个点之间的连线就是 (max(a_{1},a_{2})),把每个点和周围点的连线存储起来作为边。
- 可以通过对每条边按照权值进行排序,那么每次对两个连通块进行合并,只要当前询问的两个点分别在这两个连通块内,答案就是当前新加入的权值。
- 在合并时考虑复杂度,就必须采用启发式合并。
代码:
int N,M,Q;
int mp[505][505];
int ans[MAXN];
int fa[MAXN];
set<int>st[MAXN];
struct Node{
int u,v,w;
bool operator < (const Node &a) const{
return w<a.w;
}
}e[MAXN];
int hashd(int x,int y){
return (x-1)*M+y;
}
int findfa(int x)
{
if(fa[x]==x){
return x;
}else{
return fa[x]=findfa(fa[x]);
}
}
void merge(int u,int v,int w)
{
//st[v] > st[u]
if(st[u].size()>st[v].size())swap(u,v);
for(auto num:st[u]){
if(st[v].find(num) == st[v].end()){
st[v].insert(num);
} else{
ans[num]=w;
st[v].erase(num);
}
}
fa[u]=v;
}
int main()
{
scanf("%d%d%d",&N,&M,&Q);
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
scanf("%d",&mp[i][j]);
}
}
for(int i=1;i<=Q;i++){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
if(x1==x2&&y1==y2){
ans[i]=mp[x1][y1];
continue;
}
st[hashd(x1,y1)].insert(i);
st[hashd(x2,y2)].insert(i);
}
int tot=0;
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
int now=hashd(i,j);
int d=hashd(i+1,j);
int r=hashd(i,j+1);
if(i!=N){
e[++tot]=(Node){now,d,max(mp[i+1][j],mp[i][j])};
}
if(j!=M){
e[++tot]=(Node){now,r,max(mp[i][j+1],mp[i][j])};
}
}
}
for(int i=1;i<=N*M;i++)fa[i]=i;
sort(e+1,e+tot+1);
for(int i=1;i<=tot;i++){
int u=findfa(e[i].u);
int v=findfa(e[i].v);
if(u==v)continue;
merge(u,v,e[i].w);
}
for(int i=1;i<=Q;i++){
printf("%d
",ans[i]);
}
}