300. Longest Increasing Subsequence

问题：

求给定数组中，最长递增子序列的长度。

Example:
Input: [10,9,2,5,3,7,101,18]
Output: 4 
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
 
Note:
There may be more than one LIS combination, it is only necessary for you to return the length.
Your algorithm should run in O(n2) complexity.

Follow up: Could you improve it to O(n log n) time complexity?

　　

解法：

解法一：DP(动态规划) Time：O(N^2)

dp[i]：截止到nums[i]，包含nums[i]的最长递增子序列的长度。

状态转移方程：dp[i] = max(dp[j]+1)  (所有j满足：0～i，nums[j]<nums[i])

边界：dp[0] = 1（nums[0]只有自己一个数字，最长递增子序列长度，也为 1 ）

代码参考：

class Solution {
public:
    //dp[i]:until nums[i](include nums[i]), the length of the longest increasing Subsequence
    //dp[i] = max(dp[i], dp[j]+1) (nums[j]<nums[i])
    //base:dp[0]=1
    int lengthOfLIS(vector<int>& nums) {
        int res = 0;
        vector<int> dp(nums.size(), 1);
        for(int i=0; i<nums.size(); i++) {
            for(int j=0; j<i; j++) {
                if(nums[j]<nums[i]) {
                    dp[i] = max(dp[i], dp[j]+1);
                }
            }
            res = max(res, dp[i]);
        }
        return res;
    }
};

解法二：二分查找(Binary Search)  Time：O(NlogN)

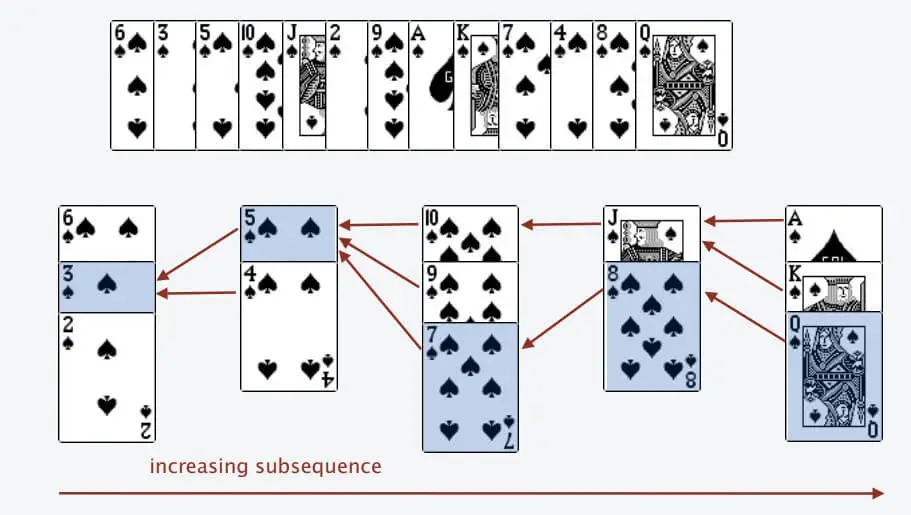
类似如下游戏：顺序抽取牌，若当前牌<顺序（i:0~res）排列的第 i 堆牌顶top，则将当前牌放入牌堆 i 的牌顶。（上面为牌底，下面为牌顶）

若直到 第res堆牌的牌顶top，都<当前牌，那么新建一个牌堆，将当前牌推入新牌堆中。

那么，这一列牌堆有如下特点：

i：0->res 牌顶为 递增数列

每一堆牌，从牌顶到牌底（由下到上）， 递增

由于每次新建牌堆，都是，所有牌顶都<当前牌，的情况下，才做的。

因此最长递增序列长度，则为 牌堆的堆数。 至少所有牌底可以构成一个满足的子序列。

那么，对于本问题，我们可以模拟该游戏，最终返回堆数res即可。

这里，在拿到当前牌，去插入牌堆的时候，对递增数列的牌顶（下），可使用二分查找。

⚠️ 注意：本题中，[2,2]的结果为 1，则说明只有完全>的数列，才为所求。

因此在上述游戏中，若找到相同的数字，则仍然合并在同一堆中，不进行新堆的创建，

因此二分查找，要找到第一个 >=当前牌 的牌堆，进行插入。 

代码参考：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int res = 0;
        vector<int> top(nums.size());
        for(int i=0; i<nums.size(); i++) {
            int poker = nums[i];
            int l = 0, r = res, mid;
            while(l<r) {
                mid = l + (r-l)/2;
                if(top[mid]>=poker) {
                    r = mid;
                }else{
                    l = mid+1;
                }
            }
            if(l==res) res++;
            top[l] = poker;
        }
        return res;
    }
};