1240. Tiling a Rectangle with the Fewest Squares

问题：

给定长宽m,n的矩形，将其划分为多个正方形，最少能划分多少个。

Example 1:
Input: n = 2, m = 3
Output: 3
Explanation: 3 squares are necessary to cover the rectangle.
2 (squares of 1x1)
1 (square of 2x2)

Example 2:
Input: n = 5, m = 8
Output: 5

Example 3:
Input: n = 11, m = 13
Output: 6
 
Constraints:
1 <= n <= 13
1 <= m <= 13

Example 1:

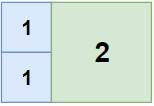
Example 2:

 

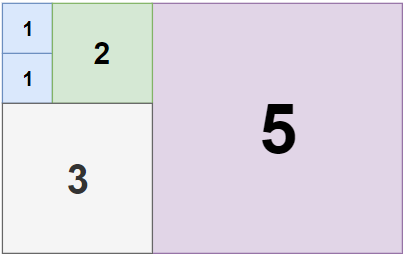
Example 3:

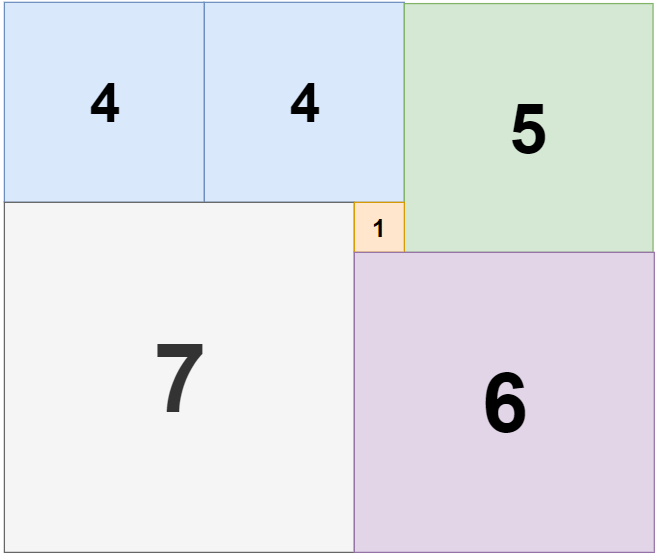
解法：DP（动态规划）Backtracking（回溯算法）

参考：LeetCode讲解

将问题划分为子问题：

将当前n*m的矩形划分方法：

方法1: 一分为二：

←正方形 [n*n] + →矩形rec [n*(m-n)] 

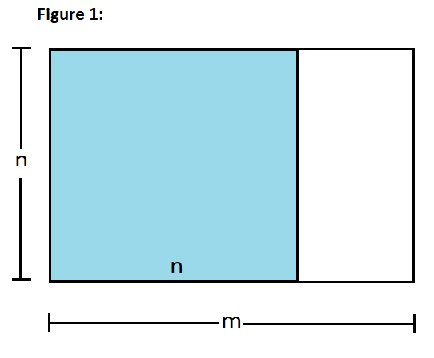
res=dp(rec) + 1(左边正方形)

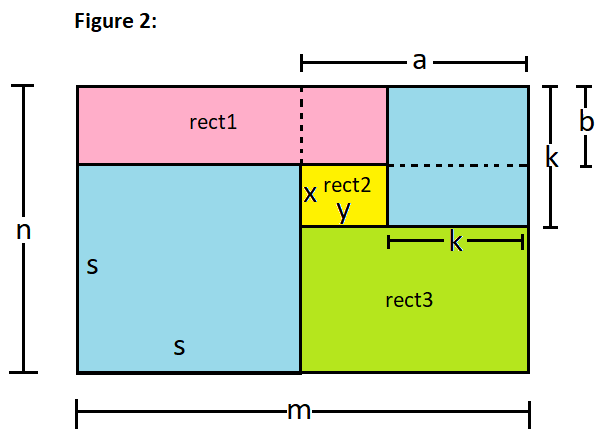
方法2:

↙️正方形 [s*s] + ↗️正方形 [k*k]

+↖️矩形rec_1 [(n-s)*(m-k)] + ↘️矩形rec_2 [(n-k)*(m-s)]  + middle小矩形rec_3 [(k-(n-s))*((m-s)-k)]

变化范围：

s：最大：n ～ 最小：0

k：最大：min((m-s)横, n高) ～ 最小：超过(n-s)高b虚线

res=dp(rec_1)+dp(rec_2)+dp(rec_3) + 2(两个正方形)

 base case：（我们确定n<=m）

• m==0 | | n==0 -> 0 不存在方块
• m==n -> 1 恰好一个正方形
• n==1 -> m 只能分成m个正方形

代码参考：

class Solution {
public:
    int count = 0;
    void print_intend() {
        for(int i=0; i<count; i++) {
            printf("  ");
        }
        return;
    }
    vector<vector<int>> dp;
    int dfs(int n, int m) {//dfs(short,long)
        if(n>m) swap(n,m);
        print_intend();
        printf("n:%d m:%d
", n,m);
        //if (n,m) has been solved
        if(dp[n][m]!=-1) {
            print_intend();
            printf("return dp[n][m]:%d
", dp[n][m]);
            return dp[n][m];
        }
        //base case:
        // 1.m=0 || n=0
        if(m==0 || n==0) {
            print_intend();
            printf("return 0
");
            return 0;
        }
        // 2.n=m -> square
        if(m==n) {
            print_intend();
            printf("return 0
");
            return 1;
        }
        // 3.n=1 -> m squares
        if(n==1) {
            print_intend();
            printf("return m:%d
", m);
            return m;
        }
        
        count++;
        //other case: res=min(case_1,case2...)
          //case_1: cut rec to left(square) & right subrec (cause:n<m, ignore up & down)
        int res = dfs(n,m-n) + 1;
          //case_2: cut rec to 
          //left-down(square) & right-up(square) [BLUE] s*s & k*k
          //left-up(rec_1) & right-down(rec_2) & middle(rec_3) [RED][GREEN][YELLOW]
          //(n-s)*(m-k)    & (m-s)*(n-k)       & (k-(n-s))*((m-s)-k)
        int rec_1, rec_2, rec_3;
        int ans = INT_MAX;
        for(int s=n-1; s>0; s--) {
            for(int k=min(n,m-s); k>=n-s; k--) {
                rec_1 = dfs(n-s, m-k);
                rec_2 = dfs(m-s, n-k);
                rec_3 = dfs(k-(n-s), (m-s)-k);
                ans = min(ans,rec_1+rec_2+rec_3+2);
            }
        }
        res = min(res, ans);
        dp[n][m] = res;
        print_intend();
        printf("return ans_res:%d, dp[%d][%d]
", res, n, m);
        count--;
        return res;
    }
    
    
    int tilingRectangle(int n, int m) {
        int x = min(n,m);//short
        int y = max(n,m);//long
        int res;
        //initialize dp:
        //dp[0][0]~dp[n+1][m+1] -> all cell = -1
        dp.resize(x+1);
        for(auto& d:dp) {
            d.resize(y+1, -1);
        }
        res = dfs(x,y);//dfs(short,long)
        return res;
    }
};