问题:
给定一个无向图,graph[i]={a,b,c...}
代表:节点 i 的邻接节点有 节点 a,b,c...
⚠️ 这里若有graph[a]中包含b,那么graph[b]中也包含a。
求将这个图中的节点分为两个集合,
任意相邻两个节点,都分别位于两个集合中。
是否能行。
Example 1:
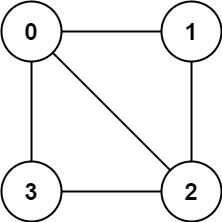
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
Example 2:
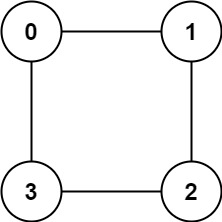
Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
Constraints:
graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] does not contain u.
All the values of graph[u] are unique.
If graph[u] contains v, then graph[v] contains u.
example 1:
example 2:
解法:BFS
本问题为图的涂色问题。
相邻两节点涂不同色。
- 涂色为 1 为一组
- 涂色为 -1 为另一组
- 初始:visited[i]都为0
由于图中可能存在独立的节点(不与任何节点相连)
所以需要遍历所有节点。
base:
对每个未访问过的节点,进行涂色check
对于第一个节点,没有任何限制,因此涂色为1.
将节点和涂色信息加入queue:
q.push({node, 1})
对队列进行遍历,
- 对每个出队节点cur
- 若该节点已经访问过,那么之前安排的set是否为queue中记录的set
- if visited[cur] == cur_sN
- 那么该点没问题,进行队列下一个点的pop。
- 但是若 if visited[cur] != cur_sN
- 说明之前标记过的组与现阶段的组不一致,返回false。check结束。
- if visited[cur] == cur_sN
- 若该节点没有访问过,那么此时标记访问过,visited[cur]=cur_sN
- 进行相邻节点的入队:(标记相反颜色)
- q.push({nextn, -cur_sN})
代码参考:
1 class Solution { 2 public: 3 4 bool check(int root, vector<vector<int>>& graph, vector<int>& visited) { 5 queue<pair<int,int>> q;//node,setNo 6 q.push({root, 1}); 7 int cur_n, cur_sN; 8 while(!q.empty()) { 9 int sz=q.size(); 10 for(int i=0; i<sz; i++) { 11 cur_n = q.front().first; 12 cur_sN = q.front().second; 13 q.pop(); 14 if(visited[cur_n]) { 15 if(visited[cur_n]!=cur_sN) return false; 16 else continue;//visited this node and it's in correct set. 17 } else { 18 visited[cur_n] = cur_sN; 19 } 20 for(auto ed:graph[cur_n]) { 21 q.push({ed, -cur_sN}); 22 } 23 } 24 } 25 return true; 26 } 27 bool isBipartite(vector<vector<int>>& graph) { 28 int n = graph.size(); 29 vector<int> visited(n,0);//setNo 30 for(int i=0; i<n ;i++) { 31 if(!visited[i] && check(i, graph, visited) == false) return false; 32 } 33 return true; 34 } 35 };