787. Cheapest Flights Within K Stops

问题：

给定n个地点，以及地点之间的航班和费用。

求从src到dst，中转最多k次以内，花费最少的费用。

Example 1:
Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200
Explanation: 
The graph looks like this:
The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.

Example 2:
Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
Output: 500
Explanation: 
The graph looks like this:
The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.
 

Constraints:
The number of nodes n will be in range [1, 100], with nodes labeled from 0 to n - 1.
The size of flights will be in range [0, n * (n - 1) / 2].
The format of each flight will be (src, dst, price).
The price of each flight will be in the range [1, 10000].
k is in the range of [0, n - 1].
There will not be any duplicated flights or self cycles.

　　

example 1:

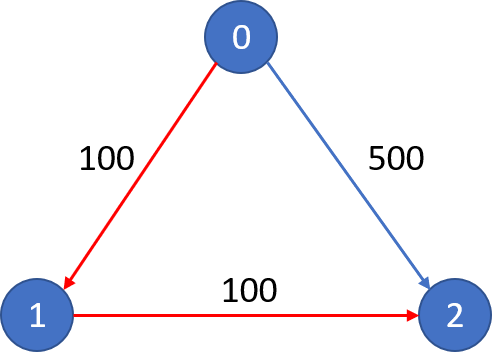
example 2:

解法一：BFS

将从src到node i的cost存入queue。

{node i, cost}

由于题目限制中转站点数 k

因此需要对queue的遍历，通过层次区分。

⚠️ 注意：在层次区分的问题中，不能使用优先队列 priority_queue，由于其会打乱节点的层次顺序。

使用dist数组保存，src到每个节点的最小距离。

在 k 层以内，按层，随时更新该距离 为最小。

⚠️ 注意：queue的遍历，不能因为遍历到dst节点就停止，由于之后还可能存在花费更少的路径，只是中转需要更多的情况。

因此到达 k 层遍历之前，要一直遍历queue，直到queue遍历结束。

若dist[dst]==INT_MAX， 则没有src->dst的路径。返回-1，否则返回dist[dst]

代码参考：

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
        int res=-1;
        if(src==dst) return 0;
        vector<vector<vector<int>>> graph(n,vector<vector<int>>());
        for(vector<int>& flt:flights) {
            graph[flt[0]].push_back({flt[1],flt[2]});
            //printf("graph[%d]_insert:{%d,%d}
", flt[0], flt[1], flt[2]);
        }
        queue<pair<int,int>> q;//stop, cost
        vector<int> dist(n, INT_MAX);
        q.push({0,src});
        dist[src] = 0;
        int cur_s, cur_cost;
        int count = 0;
        while(!q.empty()) {
            int sz = q.size();
            for(int i=0; i<sz; i++) {
                cur_cost = q.front().first;
                cur_s = q.front().second;
                q.pop();
                //until k steps, can't return. 
                //cause there maybe a less cost way which may spend more steps.
                //if(cur_s==dst) return min(dist[dst], cur_cost);
                //printf("cur_s:%d cur_cost:%d
", cur_s, cur_cost);
                for(auto next:graph[cur_s]) {
                    //printf("graph[%d] ", cur_s);
                    //printf("next[0]:%d, next[1]:%d
", next[0], next[1]);
                    if(dist[next[0]] > cur_cost+next[1]) {
                        //printf("INSERT next[0]:%d, cur_cost+next[1]:%d+%d
", next[0], cur_cost,next[1]);
                        dist[next[0]] = cur_cost+next[1];
                        q.push({dist[next[0]], next[0]});
                    }
                }
            }
            if(count>=K) return dist[dst]==INT_MAX?-1:dist[dst];
            //printf("count:%d

", count);
            count++;
        }
        return dist[dst]==INT_MAX?-1:dist[dst];
    }
};

解法二：优先队列 priority_queue

上述解法中，解释了层级相关的问题，不能使用优先队列，

但如果将层级关系作为变量，保存至queue中，在K以内的所有情况，cost的更新（选取最短距离）都是不限于层级关系的，

满足K以内的情况，才保存在queue中进行处理，即可规避该问题。

使用了优先队列，那么可保证先处理的一定是距离最短的节点，

若先找到dst，即可返回。

代码参考：

typedef tuple<int, int, int> ti;
class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
        if(src==dst) return 0;
        vector<vector<vector<int>>> graph(n);
        for(vector<int>& flt:flights) {
            graph[flt[0]].push_back({flt[1],flt[2]});
        }
        priority_queue<ti, vector<ti>, greater<ti>> q;//cost,stop,K(level)
        q.push({0,src, K+1});
        int cur_s, cur_cost, cur_k;
        while(!q.empty()) {
            auto [cur_cost, cur_s, cur_k] = q.top();
            q.pop();
            if(cur_s==dst) return cur_cost;
            if(!cur_k) continue;//level > K, invalid route
            for(auto next:graph[cur_s]) {
                q.push({cur_cost+next[1], next[0], cur_k-1});
            }
        }
        return -1;
    }
};