882. Reachable Nodes In Subdivided Graph

问题：

给定一个无向图，n个节点

每条边可分为0个or多个node，

求从节点0开始，走maxMoves步，总共能经过多少个node。

Example 1:
Input: edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3
Output: 13
Explanation: The edge subdivisions are shown in the image above.
The nodes that are reachable are highlighted in yellow.

Example 2:
Input: edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], maxMoves = 10, n = 4
Output: 23

Example 3:
Input: edges = [[1,2,4],[1,4,5],[1,3,1],[2,3,4],[3,4,5]], maxMoves = 17, n = 5
Output: 1
Explanation: Node 0 is disconnected from the rest of the graph, so only node 0 is reachable.
 
Constraints:
0 <= edges.length <= min(n * (n - 1) / 2, 104)
edges[i].length == 3
0 <= ui < vi < n
There are no multiple edges in the graph.
0 <= cnti <= 104
0 <= maxMoves <= 109
1 <= n <= 3000

　　

example 1:

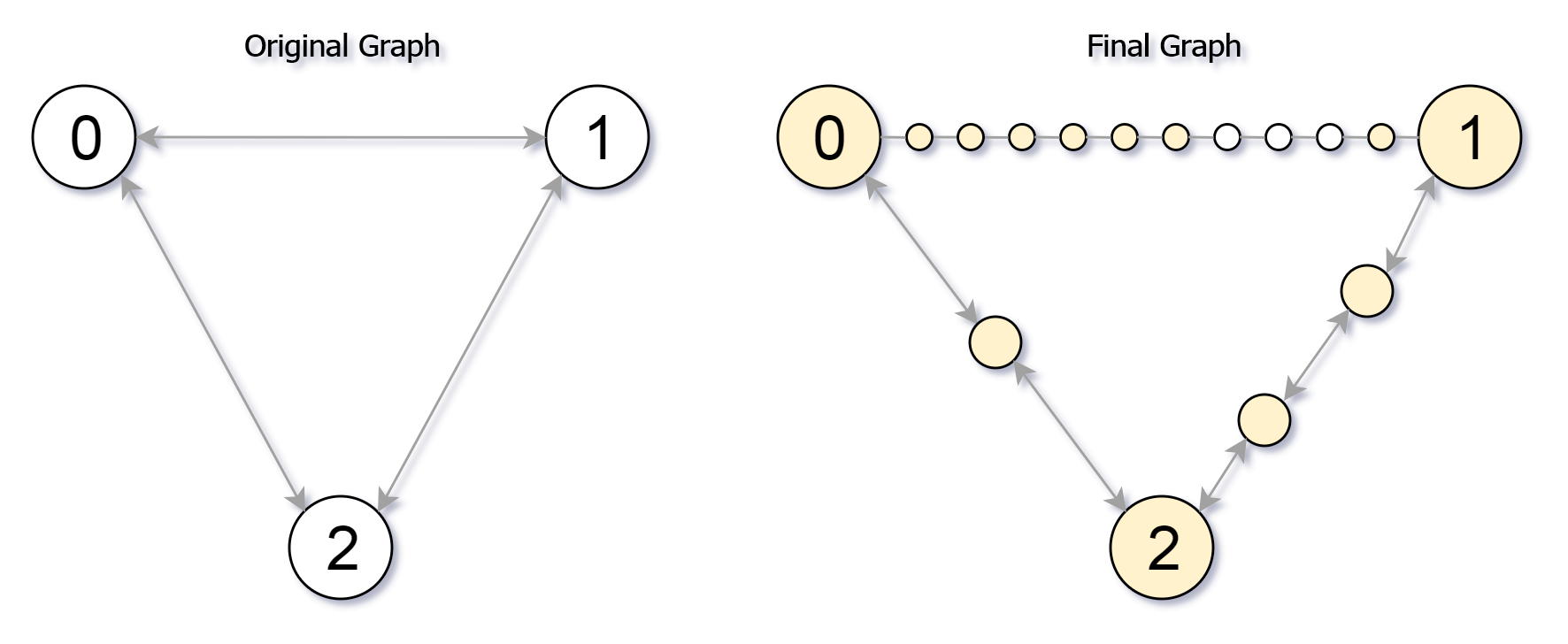
解法：Dijkstra 最小路径

思路：

• 对于本题，题意：要求最多能经过多少点。
  • 可转化为：
  • 求0节点到各个节点的最短距离 + 到达每个节点后剩余的步数。
  • 因为：求到各个节点到【最短】距离，那么可以尽可能多的走到节点 + 且使得其剩余的步数更多。

• 使用dis数组记录，到达每个节点剩余的步数。
  • 那么，遍历所有的边，对每条边：剩余步数★：
  • 所求为：min{ 两个节点剩余步数之和, 两节点间的距离 }
  • (去除重复计算的中间节点)
• 最终结果res 
  • 能到达的各个节点数：dis.size
  • + 各条边的 剩余步数★。

要求dis[]（0到各个节点的剩余步数）：Dijkstra

• 使用优先队列，优先pop剩余步数更大的（也就是到达节点cost最小的）
  • 大->小：less
• 每次pop一个节点，对该节点进行处理：
  • 如果该节点已经记录过dis，那么跳过
  • 否则，记录该节点dis
    • 然后再展开该节点，看下一个节点next：
      • 若dis[next]记录过，那么跳过。
    • 下一个节点：leftmoves= cur.leftmoves-cur_next_cost - 1(节点自己)
      • 若leftmoves<0那么无法到达next，跳过。
    • 其他记录next到queue。

⚠️ 注意：Dijkstra算法中，每pop处理一个节点再进行dis记录。

防止在同层入队排序前，就阻止了更小的节点记录。

代码参考：

class Solution {
public://Dijkstra:shortest route to every node
    //->to get more [left moves] after arrived node.
    
    //conclusion: for every edge, which one of two node has left moves.
    //res = add{all these left moves} + Count(every reachable node(leftmoves>0)).
    
    //if both two nodes have left moves and these 2 moves duplicated in the middle.
    // we just need the all moves between this two nodes. cnti[node1][node2]
    // namely: min(leftmoves[node1]+leftmoves[node2], cnti[node1][node2])
    typedef pair<int,int> pii;
    int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
        int res = 0;
        priority_queue<pii,vector<pii>,less<pii>> q;//leftmoves, nodeid
        //less: first to pop the max value.
        //greater: first to pop the min value.
        //we need to pop max left, as to say the cost is min.
        unordered_map<int, int> dis;//nodeid, leftmoves;
        //undirected map->save both two node.
        vector<unordered_map<int, int>> graph(n);
        //graph[i]:{{node j1, moves1}{node j2, move2}...}
        for(auto e:edges) {
            graph[e[0]][e[1]]=e[2];
            graph[e[1]][e[0]]=e[2];
        }
        //base:
        q.push({maxMoves, 0});
        //dis[0] = maxMoves;
        pii cur;
        while(!q.empty()) {
            cur = q.top();
            q.pop();
            if(dis.count(cur.second)) continue;
            dis[cur.second] = cur.first;
            cout<<"node:"<<cur.second<<" leftmove:"<<dis[cur.second]<<endl;
            for(auto nextn:graph[cur.second]) {
                int leftmoves = cur.first-nextn.second-1;
                if(dis.count(nextn.first) || leftmoves<0) continue;
                q.push({leftmoves, nextn.first});
                //dis[nextn.first] = leftmoves;
            }
        }
        
        res = dis.size();
        for(auto e:edges) {
            int node1 = dis.count(e[0])?dis[e[0]]:0;
            int node2 = dis.count(e[1])?dis[e[1]]:0;
            res += min(node1+node2, e[2]);
        }
        return res;
    }
};