909. Snakes and Ladders

问题：

给定n*n的二维数组，

board[i][j]：每个格子代表，到达该格子后的下一个位置。

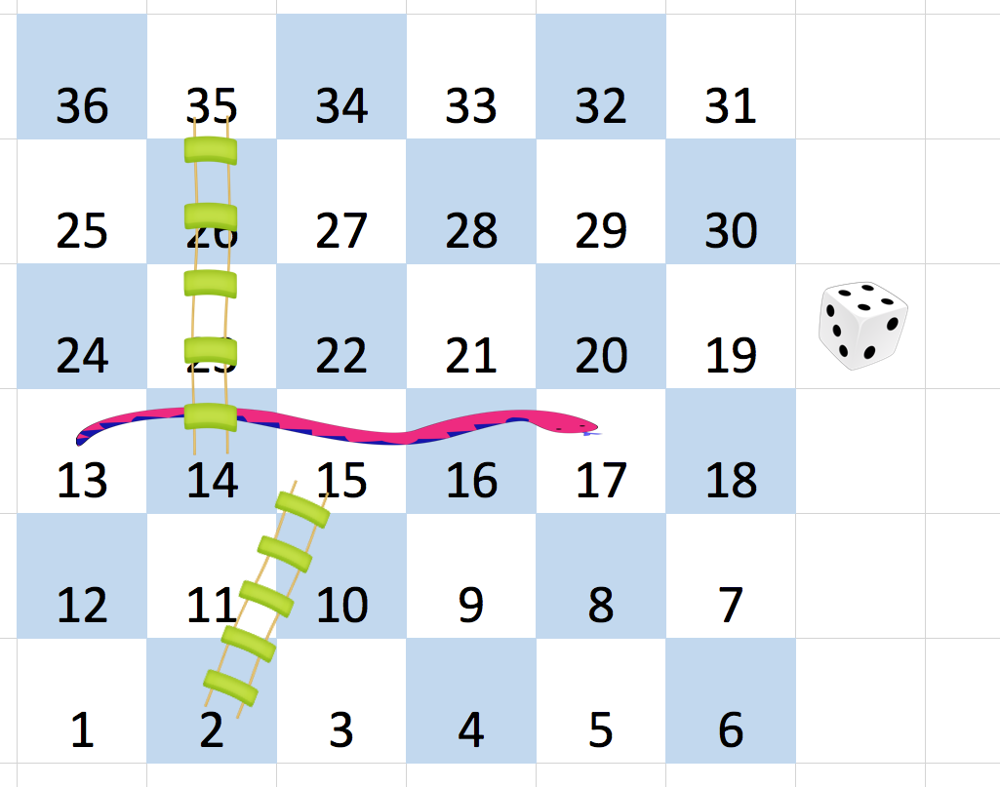
⚠️ 注意：位置标记：从最后一行第一个开始，标记为 1 开始，成Z字形向上，依次递增。直到第一行第一个格子位置为 n*n。

• 若board[i][j]==-1，（假设当前位置标记为x）那么它的下一个位置可以为x+1～x+6任意一个（不能超过n*n）
• 若board[i][j]!=-1，那么下一个位置即为所示标记位置。（我们将这种看作快捷路径，蛇or梯子）

求，从位置 1 开始，最少走多少步，能够到达 n*n 位置（最后一个格子）

若不能到达，返回-1

Example 1:
Input: [
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,35,-1,-1,13,-1],
[-1,-1,-1,-1,-1,-1],
[-1,15,-1,-1,-1,-1]]
Output: 4
Explanation: 
At the beginning, you start at square 1 [at row 5, column 0].
You decide to move to square 2, and must take the ladder to square 15.
You then decide to move to square 17 (row 3, column 5), and must take the snake to square 13.
You then decide to move to square 14, and must take the ladder to square 35.
You then decide to move to square 36, ending the game.
It can be shown that you need at least 4 moves to reach the N*N-th square, so the answer is 4.

Note:
2 <= board.length = board[0].length <= 20
board[i][j] is between 1 and N*N or is equal to -1.
The board square with number 1 has no snake or ladder.
The board square with number N*N has no snake or ladder.

　　

解法：BFS

首先，将board二维数组，映射到 如题意所述的位置标记 一维数组。route

queue入队位置标记 1。

visited标记 1。

对每个当前处理的位置，next：有x+1～x+6，6种选择，

其中如果route[x+i]!=-1 那么x+i的这个目的地修改为route[x+i]

再进行next入队。

遍历queue。每层即为一步。steps++

当当前位置==n*n，return steps。

代码参考：

class Solution {
public:
    /*void print_vector(vector<int>& rout) {
        cout<< "{" ;
        for(auto r:rout) {
            cout<< r <<",";
        }
        cout<< "}" <<endl;
    }*/
    int snakesAndLadders(vector<vector<int>>& board) {
        int n = board.size();
        int steps = 0;
        vector<int> route(n*n+1);
        int k=1;
        for(int i=n-1; i>=0; i--) {
            for(int j=0; j<n; j++) {
                if((n-i)%2) route[k] = board[i][j];
                else route[k] = board[i][n-j-1];
                k++;
            }
        }
        //print_vector(route);
        queue<int> q;
        unordered_set<int> visited;
        q.push(1);
        visited.insert(1);
        while(!q.empty()) {
            int sz = q.size();
            for(int i=0; i<sz; i++) {
                int cur = q.front();
                q.pop();
                if(cur == n*n) return steps;
                for(int i=1; i<7; i++) {
                    if(cur+i>n*n) continue;
                    int next = route[cur+i];
                    if(next==-1) next = cur+i;
                    if(visited.insert(next).second) {
                        q.push(next);
                    }
                }
            }
            steps++;
        }
        return -1;
    }
};