1368. Minimum Cost to Make at Least One Valid Path in a Grid

问题：

给定n*m二维数组grid，要求从左上角(0,0)->右下角(n-1,m-1)

移动规则：grid[i][j]

1：right -> grid[i][j + 1]

2：left -> grid[i][j - 1]

3：down -> grid[i + 1][j]

4：up -> grid[i - 1][j]

若按照grid[i][j]所述的方式移动，无消耗。

否则可改变为余下的移动方向，则消耗为 1。

求要到达目标位置，最小消耗是多少。

Example 1:
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:
Input: grid = [[1,2],[4,3]]
Output: 1

Example 4:
Input: grid = [[2,2,2],[2,2,2]]
Output: 3

Example 5:
Input: grid = [[4]]
Output: 0
 

Constraints:
m == grid.length
n == grid[i].length
1 <= m, n <= 100

　　

example 1:

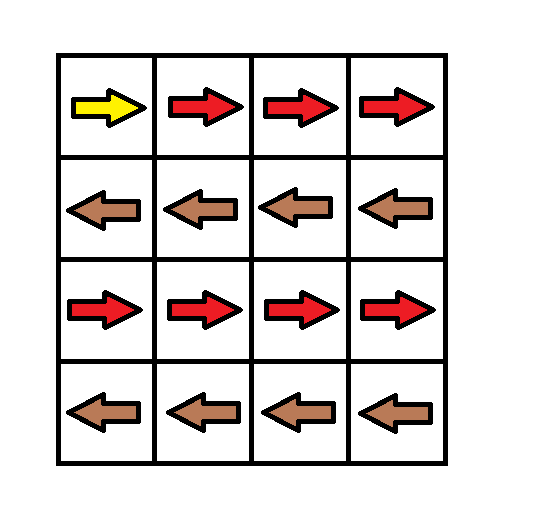
example 2:

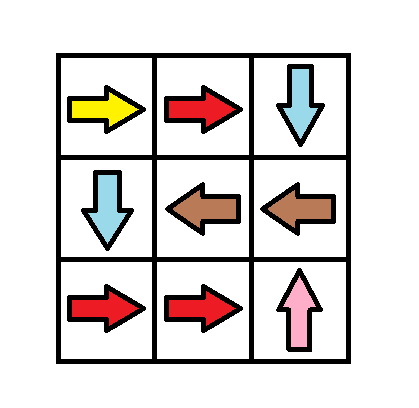
 example 3:

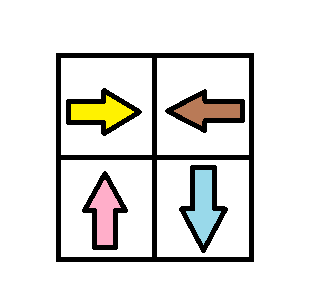
解法：BFS，Dijkstra，priority queue

使用优先队列，权值为：cost

优先处理cost较小的状态。

• 状态：cell坐标
  • visited也保存cell坐标，
    • ⚠️ 注意：但是由于可能会重复到达同一个坐标，cost不同，那么选择cost更小的路径，这里即用到了（从(0,0)到当前cell的）最短路径。
    • 因此visited保存：到对应cell的cost：unordered_map<int, int> //i*100+j, cost
  • queue里保存：权值cost，cell坐标 (i, j)

• 对当前状态的处理：
  • 如果cell坐标==target，那么返回当前权值cost
  • 否则，进行下一步选择：
    • dir四个方向：若!=gird[当前cell坐标]，cost++
    • 若next cell的visited中保存的cost更小，那么选择当前的路径到达next cell。更新visited[next cell]
    • 同时将next cell的状态push到优先队列中。

代码参考：

class Solution {
public:
    vector<vector<int>> dir = {{0,0},{0,1},{0,-1},{1,0},{-1,0}};
    int m,n;
    int minCost(vector<vector<int>>& grid) {
        n = grid.size();
        m = grid[0].size();
        priority_queue<pair<int, pair<int,int>>, vector<pair<int,pair<int,int>>>, greater<pair<int,pair<int,int>>>>q;
        //cost, {i,j}
        unordered_map<int,int> visited;//i*100+j, cost
        q.push({0,{0,0}});
        visited[0]=0;
        while(!q.empty()) {
            auto [cur_cost, cur] = q.top();
            q.pop();
            //cout<<"pop: cost:"<<cur_cost<<"{x,y}: "<<cur.first<<","<<cur.second<<endl;
            if(cur.first == n-1 && cur.second == m-1) return cur_cost;
            for(int i=1; i<5; i++) {
                int x = cur.first+dir[i][0];
                int y = cur.second+dir[i][1];
                int cost = cur_cost;
                if(x<0 || y<0 || x>=n || y>=m) continue;
                if(grid[cur.first][cur.second]!=i) cost++;
                if(visited.count(x*100+y) == 0 || visited[x*100+y]>cost) {
                    visited[x*100+y] = cost;
                    q.push({cost, {x,y}});
                    //cout<<"push: cost:"<<cost<<"{x,y}: "<<x<<","<<y<<endl;
                }
            }
        }
        return m+n-2;
    }
};