1319. Number of Operations to Make Network Connected

问题：

给定n个节点，和节点之间的连线关系connections。

若其中有多余的连线，可用于连接任意不相连的节点，使得所有节点相连。

求若可以，至少需要多少条连线。

不可以，返回-1。

Example 1:
Input: n = 4, connections = [[0,1],[0,2],[1,2]]
Output: 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.

Example 2:
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
Output: 2

Example 3:
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
Output: -1
Explanation: There are not enough cables.

Example 4:
Input: n = 5, connections = [[0,1],[0,2],[3,4],[2,3]]
Output: 0
 
Constraints:
1 <= n <= 10^5
1 <= connections.length <= min(n*(n-1)/2, 10^5)
connections[i].length == 2
0 <= connections[i][0], connections[i][1] < n
connections[i][0] != connections[i][1]
There are no repeated connections.
No two computers are connected by more than one cable.

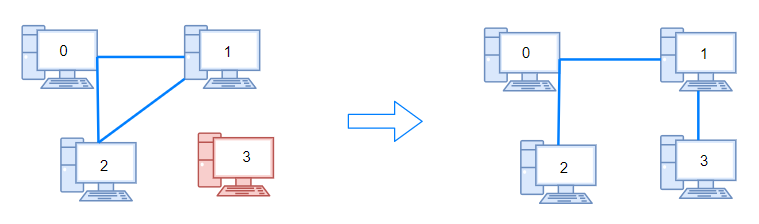
example 1:

​

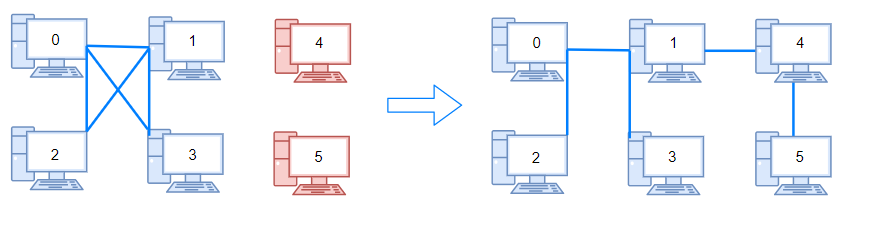
example 2:

​

解法：DFS，Union find

思路：

• 将所有节点，单独看作一个group。
• 然后，对各个节点，进行DFS，若访问过，标记visited。

处理：

• 对于外部所有节点进行访问时，若当前节点未被访问过，返回为1。
  • 代表这个节点为一个全新的group。
  • 在对第一个节点访问的过程中，同时DFS访问了与他关联的所有节点，标记visited。
• 因此，在外部进行下一个节点访问时，若该节点已被访问，那么无法返回：此节点为全新group的 1，只能返回 0。
  • 表示这个节点为已经存在group中的节点。
• 统计所有节点共有多少个全新的group。
• 那么所需的连线即为：group-1 条。

在初始状况下，connections提供的唯一连线中，若少于节点数-1条连线，那么无法出现多余的连线，去弥补独立group直接的连接。

DFS：

• 状态：
  • 当前节点 id：i
• 退出条件：
  • 已被标记visited。return 0。
• 选择：
  • 该节点 i 的所有下一个节点。
• 处理：
  • 标记该节点访问，且返回 1，return 1。

代码参考： 

class Solution {
public:
    unordered_map<int,vector<int>> conMap;
    unordered_set<int> visited;
    int dfs(int i) {
        if(!visited.insert(i).second) return 0;//already visited.
        //not visited
        for(auto cM:conMap[i]) {
            dfs(cM);
        }
        return 1;
    }
    int makeConnected(int n, vector<vector<int>>& connections) {
        //**There are no repeated connections.
        //then: at least need (node - 1) lines.
        if(connections.size()<n-1) return -1;
        for(auto con:connections) {
            conMap[con[0]].push_back(con[1]);
            conMap[con[1]].push_back(con[0]);
        }
        int res=0;
        for(int i=0; i<n; i++) //get the number of connected nodes' groups.
            res += dfs(i);
        res-=1;//the number of lines needed is: SUM(groups)-1;
        return res;
    }
};