96. Unique Binary Search Trees

问题：

给定1～n个节点，构成（前序，中序，后序，其中任意一种）遍历的序列，

求可构成的二叉树的种类个数。

Example 1:
Input: n = 3
Output: 5

Example 2:
Input: n = 1
Output: 1
 
Constraints:
1 <= n <= 19

　　

example 1:

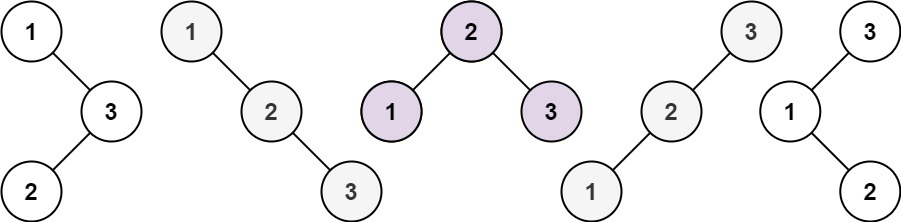
解法：Binary Tree（二叉树），DP（动态规划）

1.状态：

• 1～i 个节点

2.选择：

• 将q作为root节点：q可以取1～i
• 当q选好后，
• 两个子树：分别有节点个数：
  • q-1个：dp[q-1]
  • i-q个：dp[i-q]

3.dp[i]

• 代表：1～i个节点，可构成二叉搜索树的种数。

4.状态转移：

• dp[i]=SUM { q:(1～i)
  • dp[q-1]*dp[i-q]
• }

5.base

• dp[1]=1：一个节点：一种
• dp[0]=1：空树：一种

代码参考：

class Solution {
public:
    //dp[i]: the num of BSTs which 1~i can struct.
    //opt: SUM {
    //   q=1~i as root
    //dp[q-1] * dp[i-q]
    //}
    //base: dp[0]=1->for x not to be 0
    //dp[1]=1
    int numTrees(int n) {
        vector<int> dp(n+1, 0);
        dp[0] = dp[1] = 1;
        for(int i=2; i<=n; i++) {
            for(int q=1; q<=i; q++) {
                dp[i] += (dp[q-1]*dp[i-q]);
            }
        }
        return dp[n];
    }
};