1. 题目描述:
在一排多米诺骨牌中,A[i] 和 B[i] 分别代表第 i 个多米诺骨牌的上半部分和下半部分。(一个多米诺是两个从 1 到 6 的数字同列平铺形成的 —— 该平铺的每一半上都有一个数字。)
我们可以旋转第 i 张多米诺,使得 A[i] 和 B[i] 的值交换。
返回能使 A 中所有值或者 B 中所有值都相同的最小旋转次数。
如果无法做到,返回 -1.
示例 1:
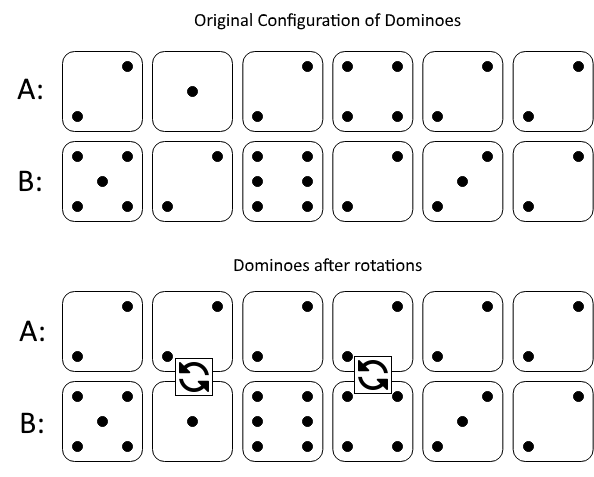
输入:A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
输出:2
解释:
图一表示:在我们旋转之前, A 和 B 给出的多米诺牌。
如果我们旋转第二个和第四个多米诺骨牌,我们可以使上面一行中的每个值都等于 2,如图二所示。
示例 2:
输入:A = [3,5,1,2,3], B = [3,6,3,3,4]
输出:-1
解释:
在这种情况下,不可能旋转多米诺牌使一行的值相等。
2. 解题思路
2.1 C++
2.1.1 方法一
解题思路:
使用两个for循环
第一个for循环:用来存储A和B的数字出现的次数,在同一个多米诺骨牌的上半部分和
下半部分相同只算一次,并在同一个位置判断上半部分和下半部分是否有满足等于i+1的
元素,若有,继续循环;若无,结束循环。
第二个for循环:用来计算上半部分和下半部分出现key(最大相同数)的次数。
1 class Solution { 2 public: 3 int minDominoRotations(vector<int>& A, vector<int>& B) { 4 /* 5 解题思路: 6 使用两个for循环 7 第一个for循环:用来存储A和B的数字出现的次数,在同一个多米诺骨牌的上半部分和 8 下半部分相同只算一次,并在同一个位置判断上半部分和下半部分是否有满足等于i+1的 9 元素,若有,继续循环;若无,结束循环。 10 第二个for循环:用来计算上半部分和下半部分出现key(最大相同数)的次数。 11 */ 12 13 // 获取数组长度 14 int n1 = A.size(), n2 = B.size(); 15 // 创建新的vector,用于判断和存储相同值去重后出现的次数。128: ASCII码范围:0-127 16 vector<int> C(128, 0); 17 // num1:上半部分计数。num2:下半部分计数。 18 int i = 0, num1 = 0, num2 = 0; 19 //存储最大相同数 20 int key = 0; 21 for(i = 0; i < n1; i++){ 22 // 上下部分相同,存储一次 23 if(A[i] == B[i]){ 24 C[A[i]]++; 25 // 上下位置都没有最大相同数 26 if(C[A[i]] != i + 1){ 27 return -1; 28 } 29 }else{ 30 C[A[i]]++; 31 C[B[i]]++; 32 // 上下位置都没有最大相同数 33 if(C[A[i]] != i + 1 && C[B[i]] != i + 1){ 34 return -1; 35 } 36 } 37 } 38 // 最大相同数 39 key = C[A[i-1]] == i ? A[i-1] : B[i-1]; 40 // 上下部最大相同数计数,上下部相同的不计。 41 for(int j = 0; j < n1; j++){ 42 if(A[j] != B[j]){ 43 if(A[j] == key){ 44 num1++; 45 }else{ 46 num2++; 47 } 48 } 49 50 } 51 // 输出最小旋转次数。 52 if(i == n1){ 53 return num1 >= num2 ? num2 : num1; 54 } 55 56 return -1; 57 } 58 };
2.1.2 方法二
解题思路:
选择第一块多米诺骨牌,它包含两个数字 A[0] 和 B[0];
检查其余的多米诺骨牌中是否出现过 A[0]。如果都出现过,则求出最少的翻转次数,其为将 A[0] 全部翻到 A 和全部翻到 B 中的较少的次数。
检查其余的多米诺骨牌中是否出现过 B[0]。如果都出现过,则求出最少的翻转次数,其为将 B[0] 全部翻到 A 和全部翻到 B 中的较少的次数。
如果上述两次检查都失败,则返回 -1。
1 class Solution { 2 public: 3 int check(int x, vector<int>& A, vector<int>& B, int n){ 4 int num1 = 0, num2 = 0; 5 for(int i = 0; i < n; i++){ 6 if(A[i] != x && B[i] != x){ 7 return -1; 8 } else if(A[i] != x){ // A[i] != x and B[i] == x A翻转到B 9 num1++; 10 } else if(B[i] != x){ // A[i] == x and B[i] !== x B翻转到A 11 num2++; 12 } 13 } 14 return min(num1, num2); 15 } 16 17 int minDominoRotations(vector<int>& A, vector<int>& B) { 18 int n = A.size(); 19 int min_N = check(A[0], B, A, n); 20 if(min_N != -1 || A[0] == B[0]){ 21 return min_N; 22 }else{ 23 return check(B[0], B, A, n); 24 } 25 } 26 };
2.2 Java
1 class Solution { 2 int check(int x, int[] A, int[] B, int n){ 3 int num1 = 0, num2 = 0; 4 for(int i = 0; i < n; i++){ 5 if(A[i] != x && B[i] != x){ // A[i] != x and B[i] == x A翻转到B 6 return -1; 7 }else if(A[i] != x){ // A[i] == x and B[i] !== x B翻转到A 8 num1++; 9 }else if(B[i] != x){ 10 num2++; 11 } 12 } 13 return num1 < num2 ? num1 : num2; 14 } 15 public int minDominoRotations(int[] A, int[] B) { 16 int n = A.length; 17 int min_N = check(A[0], B, A, n); 18 if(min_N != -1 || A[0] == B[0]){ 19 return min_N; 20 }else{ 21 return check(B[0], B, A, n); 22 } 23 } 24 }
2.3 Python
1 class Solution: 2 3 4 def minDominoRotations(self, A: List[int], B: List[int]) -> int: 5 def check(x, A, B, n): 6 num1 = 0 7 num2 = 0 8 for i in range(n): 9 if A[i] != x and B[i] != x: 10 return -1 11 elif(A[i] != x): 12 num1 += 1 13 elif(B[i] != x): 14 num2 += 1 15 return min(num1, num2) 16 n = len(A) 17 min_N = check(A[0], B, A, n) 18 if min_N != -1 or A[0] == B[0]: 19 return min_N 20 else: 21 return check(B[0], B, A, n)
3. 结语
努力去爱周围的每一个人,付出,不一定有收获,但是不付出就一定没有收获! 给街头卖艺的人零钱,不和深夜还在摆摊的小贩讨价还价。愿我的博客对你有所帮助(*^▽^*)(*^▽^*)!
如果客官喜欢小生的园子,记得关注小生哟,小生会持续更新(#^.^#)(#^.^#)。