1. 工作原理(定义)
二分插入排序(Binary Insertion Sort,折半插入排序 OR 拆半插入排序),采用折半查找方法。
二分查找插入排序的原理:是直接插入排序的一个变种;区别是:在有序区中查找新元素插入位置时,为了减少元素比较次数提高效率,采用二分查找算法进行插入位置的确定。
2. 算法步骤
设数组为a[0…n]。
1. 将原序列分成有序区和无序区。a[0…i-1]为有序区,a[i…n] 为无序区。(i从1开始)
2. 从无序区中取出第一个元素,即a[i],使用二分查找算法在有序区中查找要插入的位置索引j。
3. 将a[j]到a[i-1]的元素后移,并将a[i]赋值给a[j]。
4. 重复步骤2~3,直到无序区元素为0。
3. 图片演示
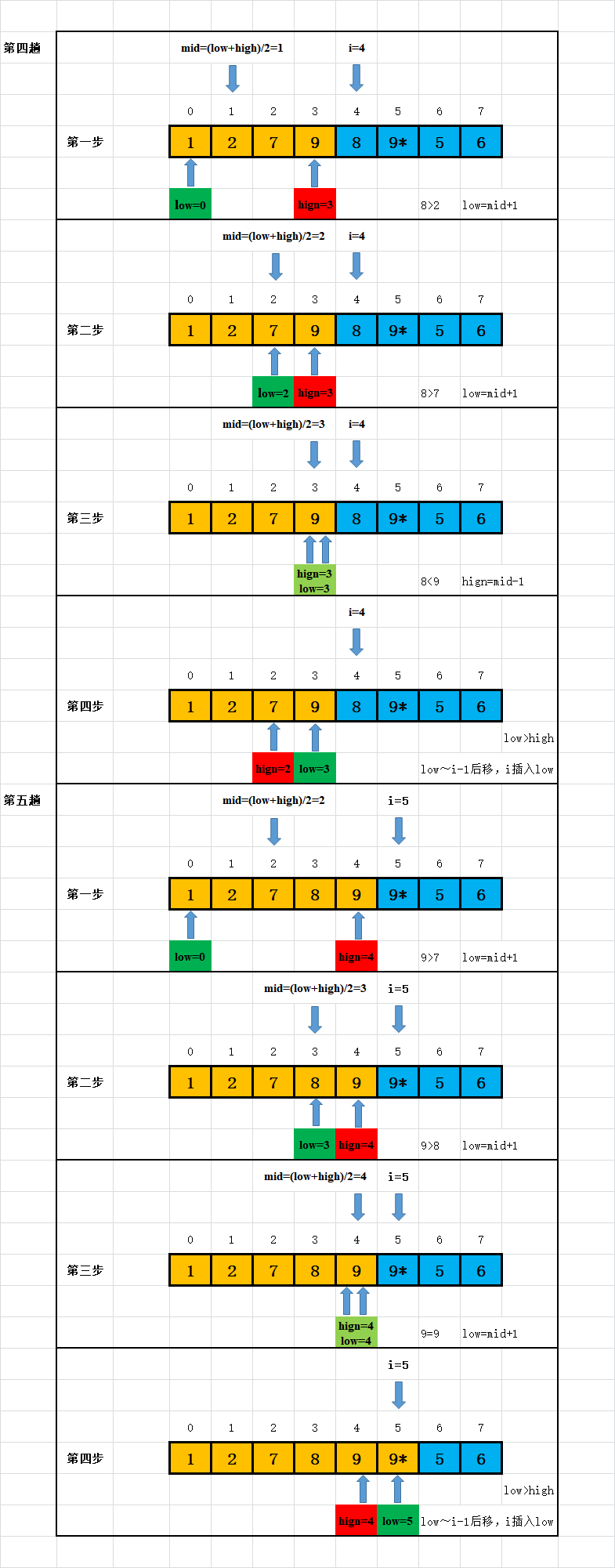
4. 性能分析
1. 时间复杂度
不难看出,折半插入排序仅仅是减少了比较元素的次数,约为O(nlogn),而且该比较次数与待排序表的初始状态无关,仅取决于表中的元素个数n;而元素的移动次数没有改变,它依赖于待排序表的初始状态。因此,折半插入排序的时间复杂度仍然为O(n²),但它的效果还是比直接插入排序要好。
最好时间复杂度O(n)
平均时间复杂度O(n²)
最坏时间复杂度O(n²)
2. 空间复杂度
插入排序过程中,需要一个临时变量temp存储待排序元素,因此空间复杂度为O(1)。
3. 算法稳定性
插入排序是一种稳定的排序算法。
4. 优缺点
- 优点 : 稳定,相对于直接插入排序元素减少了比较次数;
- 缺点 : 相对于直接插入排序元素的移动次数不变;
5. 优化
2-路插入排序算法是在折半插入排序的基础上对其进行改进,减少其在排序过程中移动记录的次数从而提高效率。
具体实现思路为:另外设置一个同存储记录的数组大小相同的数组 d,将无序表中第一个记录添加进 d[0] 的位置上,然后从无序表中第二个记录开始,同 d[0] 作比较:如果该值比 d[0] 大,则添加到其右侧;反之添加到其左侧。
使用 2-路插入排序算法对无序表{3,1,7,5,2,4,9,6}排序的过程如下:
- 将记录 3 添加到数组 d 中:
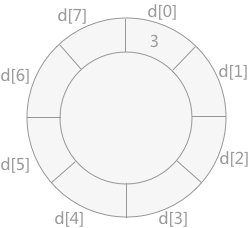
- 然后将 1 插入到数组 d 中,如下图所示:
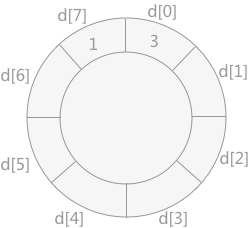
- 将记录 7 插入到数组 d 中,如下图所示:
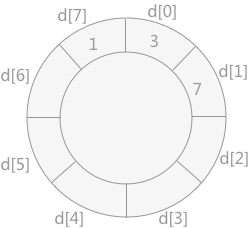
- 将记录 5 插入到数组 d 中,由于其比 7小,但是比 3 大,所以需要移动 7 的位置,然后将 5 插入,如下图所示:
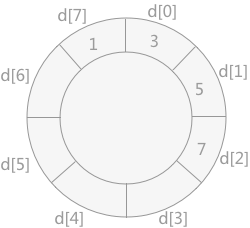
- 将记录 2 插入到数组 d 中,由于比 1大,比 3 小,所以需要移动 3、7、5 的位置,然后将 2 插入,如下图所示:
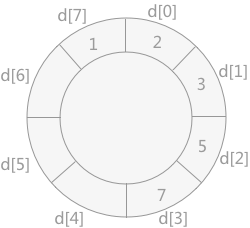
- 将记录 4 插入到数组 d 中,需要移动 5 和 7 的位置,如下图所示:
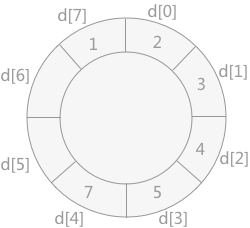
- 将记录 9 插入到数组 d 中,如下图所示:
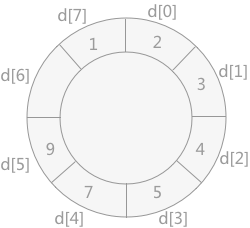
- 将记录 6 插入到数组 d 中,如下图所示:
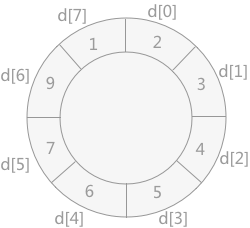
最终存储在原数组时,从 d[7] 开始依次存储。
2-路插入排序相比于折半插入排序,只是减少了移动记录的次数,没有根本上避免,所以其时间复杂度仍为O(n2)。
6. 具体代码
import java.util.Arrays; public class BinaryInsertionSort{ public static void main(String[] args) { int[] arr = {8,7,6,5,4,3,2,1}; System.out.println(Arrays.toString(binaryInsertionSort2(arr))); } // 二分插入排序 public static int[] binaryInsertionSort(int[] sourceArray) { // 对 arr 进行拷贝,不改变参数内容 int len = sourceArray.length; int[] arr = Arrays.copyOf(sourceArray, len); // 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的 for (int i = 1; i < len; i++) { int left = 0; int right = i-1; int tmp = arr[i]; // 记录要插入的数据 while(left <= right) { int mid = (left + right) / 2; //二分区域 if(arr[mid] > tmp) { right = mid - 1; //向左缩小区域 }else { left = mid + 1; //向右缩小区域,当等于的时候往后加一位,保证了稳定性 } } //arr[left,i-1]的元素整体后移 for(int j=i; j>=left+1; j--) { arr[j] = arr[j-1]; } arr[left] = tmp; } return arr; } //改进的二分插入--2路插入排序 public static int[] binaryInsertionSort2(int[] sourceArray){ int first = 0;//分别记录temp数组中最大值和最小值的位置 int last = 0; int k = 0; int len = sourceArray.length; int[] arr = Arrays.copyOf(sourceArray, len); int[] temp = new int[len]; temp[0] = arr[0]; for (int i = 1; i < len; i++){ // 待插入元素比最小的元素小 if (arr[i] < temp[first]){ first = (first - 1 + len) % len; temp[first] = arr[i]; } // 待插入元素比最大元素大 else if (arr[i] > temp[last]){ last = (last + 1 + len) % len; temp[last] = arr[i]; } // 插入元素比最小大,比最大小 else { k = (last + 1 + len) % len; //当插入值比当前值小时,需要移动当前值的位置 while (temp[((k - 1) + len) % len] > arr[i]) { temp[(k + len) % len] =temp[(k - 1 + len) % len]; k = (k - 1 + len) % len; } //插入该值 temp[(k + len) % len] = arr[i]; //因为最大值的位置改变,所以需要实时更新final的位置 last = (last + 1 + len) % len; } } // 将排序记录复制到原来的顺序表里 for (k = 0; k < len; k ++) { arr[k] = temp[(first + k) % len]; } return arr; } }
