2、自然大调
零、五声调式
介绍自然大调之前先来介绍五声调式。先来复习一下纯五度循环:
C — G — D — A — E — B — F#/Gb — C#/Db — G#/Ab — D#/Eb — A#/Bb — F — C
五声调式就是从根音开始,在五度循环上顺序找到五个音构成的。譬如中国五声调式:宫(C)、商(D)、角(E)、徵(G)、羽(A)。这五个音是五度循环上从C开始找到的五个音CGDAE,排列在一个八度以内的结果。这样在传统上称为“宫调”。值得注意的是,传统调式并非只有这五个音,实际上十二个音是齐全的,与西方古典理论的不同点,基本出发点在于“调内音”是五个还是七个的区别(下面介绍)。
一、C自然大调
五声调式是从根音沿五度循环找到5个音,而自然大调则是在这五个音之外,向两侧各扩张一个音,变成七个音,这样也就成了自然大调。例如C自然大调:F — C — G — D — A — E — B。这七个音对于C大调来讲,就是刚刚提到的“调内音”。C比较特殊,称为“主音”。剩余的五个音则叫“调外音”。如果在上一篇提到过的网格图上画出来,大体如下:
可以看到是一些具有特定形状的平行四边形,具有周期性。在图上从根音推导出调内音也是容易的:只要向左右两个方向,进行“上 — 下 — 上”的模式,推导出这种平行四边形就好了。
如果把这几个音压缩到一个八度里,就得到了CDEFGAB,即是C大调音阶。在音阶上,各个音都被标上音级,从1到7,和简谱相同。这里大家应该注意,音级只有在某个调中才有意义。
二、C大调的调内三和弦
在C大调之中构造调内三和弦,也要遵循最基本的三度规则,而且多出一条规则:只能使用调内音。观察音阶:CDEFGAB,用三度去构造三和弦,可以构造出七个三和弦。
其中大三和弦有:
C — E — G、F — A — C、G — B — D
小三和弦有:
D — F — A、E — G — B、A — C — E
剩余了一个和弦:
B — D — F
可以看到这个和弦的结构是小三度+小三度=减五度,即$3+3=6$,这样称为减三和弦,记作Bdim。这是一种不和谐的三和弦,而且减五度使得听觉效果有紧张感、阴暗。
如果我们画在网格上,就像下面这样: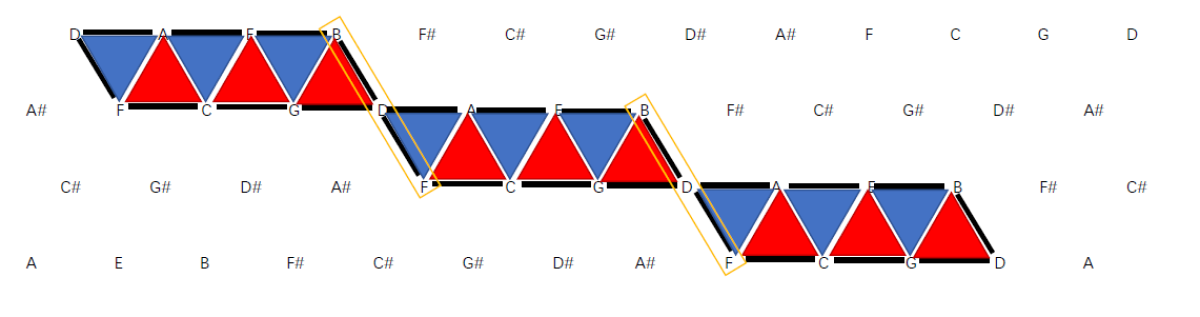
我们对某个调的调内三和弦也进行级数的编号,这里就用罗马数字来表示,而且用大写表示大三和弦,小写表示小三和弦:
Ⅰ:C — E — G
ii:D — F — A
iii:E — G — B
Ⅳ:F — A — C
Ⅴ:G — B — D
vi:A — C — E
vii-dim:B — D — F
可以发现,只有1、4、5构成了明亮的大三和弦,而2、3、6则构成小三和弦,7则只能构成减三和弦。1、4、5的主要性质,与一度、四度、五度的和谐性质有惊人的巧合。这些性质对于和弦的作用有十分重要的影响。
三、任意自然大调
上面我们用C自然大调作为例子,但我们知道,大调有12个,其它大调也有如此的性质吗?
实际上是的,因为大调的形成方式是在五度循环上连续的七个音(其中第二个是主音),因此大调之间也有周期性、循环性等性质。乐理书籍经常将“全全半全全全半”作为大调的特点,这是对的。另一种循环的表现形式就是网格图。在网格图上画出Eb大调: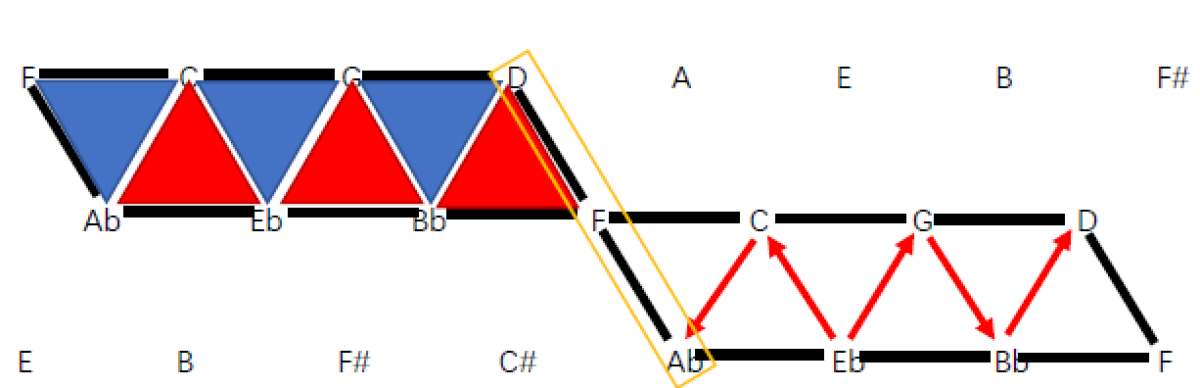
显然,只要是大调,总有这样的平行四边形结构和调内三和弦结构。在网格图上从根音生成自然大调的方式即是:向左右两个方向,进行“上 — 下 — 上”的模式,找到这个平行四边形即可。注意根音一定会在四边形的下底边。
大家注意,刚刚图中的G#、D#、A#变成了Ab、Eb、Bb,这主要是因为我们认为我们画出了Eb大调的缘故。如何确定一个大调里这些音的音名呢?主要有以下两条原则:
1、一个调式一定用上CDEFGAB所有七个字母。如果这里Ab不变,仍是G#,则G和G#重复,而A没有出现,违反了这个原则。
2、自然调式不会有升降号混用的情况。如果Ab不变仍是G#,则调式里既有#又有b,违反了这个原则。
这两个原则在自然调式里不会互斥,因此可以混合使用。这样,和弦的级数在图里也清楚了: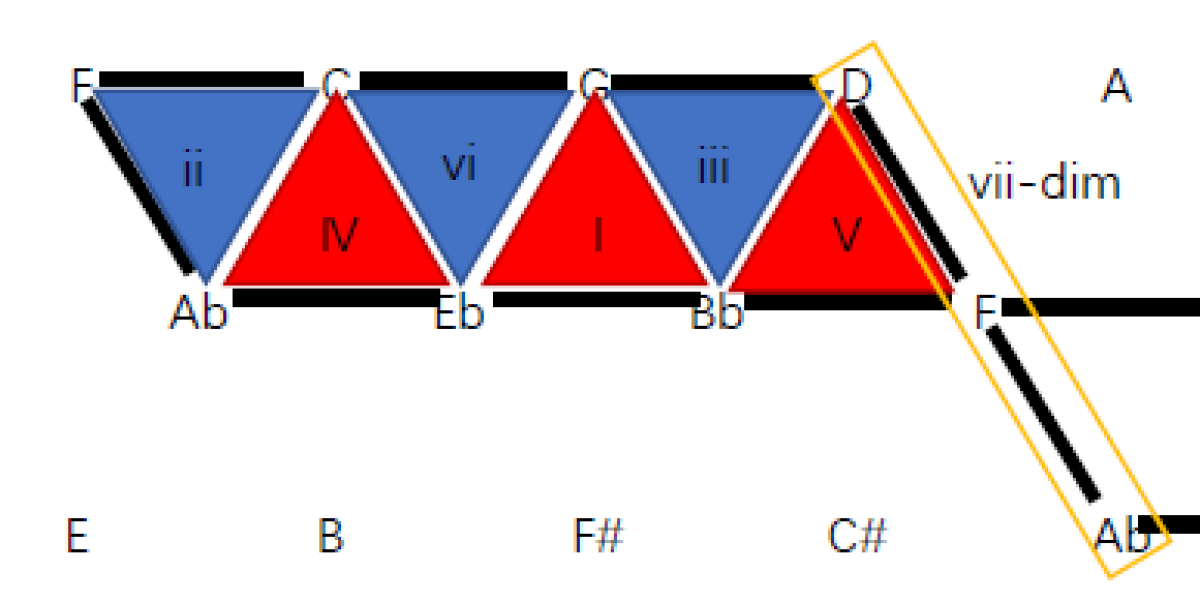
除了推导各个大调的调内音和各级三和弦,我们还可以用这张图判断某个三和弦会出现在什么大调里。只需要固定某个三和弦的三角形(或者减三和弦的线段),查看哪些平行四边形会包括这个三角形就好了。比如上面的图就让我们看到,Cmaj就不能出现在Eb大调里。这一点也可以用Eb大调里E变成了Eb来说明。
总之,三和弦网格图的神奇的性质还不止这些。利用三和弦网格图,我们可以“平等”地训练每个大调的推导,这有助于我们摆脱由于音名的习惯问题带来的“C大调依赖症”。大家可以在网格图的推导上,利用键盘乐器或App来尝试听这些和弦和大调。