在实现这个算法的时候,想法是假如有一个数组{A,B,C),之后创建一个List存储{A,A+B,A+B+C);
若要求里面最大的连续数组的时候,用List后面的第i元素减去前面的第z元素的值如果最大的话(保证连续),那就说明从位置z+1到位置i的连续数组有最大的和。然而在情况只有在特殊的情况下,最大值的位置若在最小值之后,并且最小值小于等于0的情况下,用最大值减去最小值即为连续子集最大值(保证最大),其实现的时间复杂度为O(n),若最大值位置在最小值之前,则该算法需要寻找出List数组里面的差值极大值才行。
实现的代码:
package lainxu; import java.util.ArrayList; import java.util.Collections; import java.util.List; import java.util.Scanner; public class ShowM { public static void main(String[] args) { // TODO 自动生成的方法存根 List<Integer> max=new ArrayList<Integer>(); int maxp=-1; //储存从1开始的子组和最大值的位置 Scanner it=new Scanner(System.in); int num=0; //手动输入区域 //-------------------------------------------- System.out.println("请输入你想要查找数组的长度:"); while(num<=0) //实现用户输入数组的大小 { if(it.hasNextInt()) { num=it.nextInt(); if(num<=0) { System.out.println("输入数组不能小于等于0,请重新输入"); } } else { it.next(); System.out.println("输入格式错误,请重新输入"); } } //-------------------------------------------- List<Integer> nums=new ArrayList<Integer>(); //用于储存数组 max.add(0); //添加一个max使其为0 for(int i=1;i<=num;i++) //储存数组 { //-------------------------------------------- //手动输入区域 System.out.println("请输入第"+i+"个数:"); Integer g_down=null; while(g_down==null) { if(it.hasNextInt()) { g_down=it.nextInt(); max.add(g_down+max.get(i-1)); nums.add(g_down); } else { it.next(); System.out.println("输入格式错误,请重新输入"); } } //-------------------------------------------- } System.out.println("输入的数组是"+nums.toString()); int minn=max.get(0); int minp=0; int remax=max.get(1); maxp=0; for(int i=1;i<max.size();i++) { List<Integer> max2=max.subList(0, i); int g_min=Collections.min(max2); if(max.get(i)-g_min>remax) { remax=max.get(i)-g_min; maxp=i-1; minp=max.indexOf(g_min); } } System.out.println("最大子数组和为是"+(remax-minn)+",位置为("+(minp+1)+","+(maxp+1)+")"); it.close(); } }
实验结果:

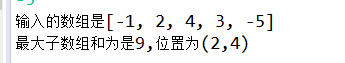



实验过程如上