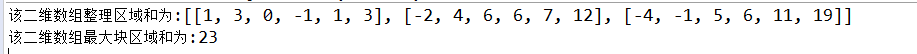该算法思路,根据我博客里面一维子数组求和的思路,可以用一个新的二维数组对该二维区域的数组进行求和,例如新的二维数组的第5个位置,就代表从1到5斜对角线的块状区域的和,即1,2,4,5这4个数的和,x个位置表示从1到x的斜对角块状区域的和,利用循环一一求出对应的和,一次循环即可,这个循环复杂度为O(nm)
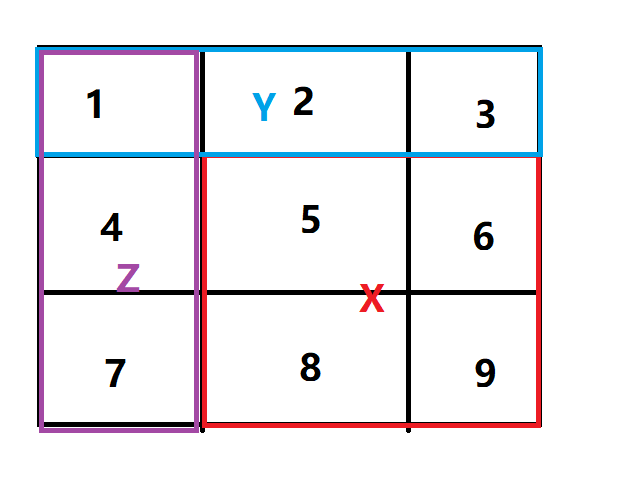
接着再求出来新的二维数组中,每一个从1到X的块状区域的和均被求出,所以对于任意区域X(如图以具体的例子展示出来),只需要求出其最大值即可。
确定一个点需要两层循环,即循环O(mn),在二维数组中需要求两个点,所以复杂度为O(m2n2)。
求值分3种(或者说4种),第1种情况即从1到X区域有最大值,这种情况在上面求和的过程中已经求出最大,所以再进行考虑。
除了不再考虑的情况,第1种最常见的情况是:
对于任意区域X要求和,只需要获得新的数组X区域右下角的值(第9个数据的值),减去Z区域的右下角的值(第7个数据),减去Y区域右下角的值(第3个数据),加上Z交Y右下角的值即可(第1个数据)。
第2种情况是块状区域包含第一行的时候有最大值,只需要求出获得X区域右下角的值减去Z区域右下角的值最大就行了
第3种情况是块状区域包含第一列的时候有最大值,只需要求出获得X区域右下角的值减去Y区域右下角的值最大就行了
根据上述的条件,实现了以下的算法如下:
package lianxu1; import java.io.IOException; import java.util.ArrayList; import java.util.Collections; import java.util.List; public class ShowSub { public static void main(String[] args) throws IOException { Integer c[][]= { {1,2,-3,-1,2,2}, {-3,4,5,1,-1,3}, {-2,-3,4,1,4,3} }; //求和 List<List<Integer>> main=new ArrayList<List<Integer>>(); for(int i=0;i<c.length;i++) { List<Integer> heng=new ArrayList<Integer>(); for(int j=0;j<c[0].length;j++) { if(j!=0) heng.add(c[i][j]+heng.get(j-1)); else heng.add(c[i][j]); } if(i!=0) main.add(addList(heng,main.get(i-1))); else main.add(heng); } //求最大值 int max=main.get(0).get(0); for(int z=0;z<main.size();z++) { int temp=Collections.max(main.get(z)); if(max<temp) { max=temp; } } //确定一位置 for(int i1=0;i1<main.size();i1++) { for(int j1=0;j1<main.get(0).size();j1++) { //确定二位置 for(int i2=i1+1;i2<main.size();i2++) { for(int j2=j1+1;j2<main.get(0).size();j2++) { int g_max=0; if(i1!=0&&j1!=0) { g_max=(main.get(i2).get(j2)+main.get(i1-1).get(j1-1)-main.get(i2).get(j1-1)-main.get(i1-1).get(j2)); } else if(i1!=0) { g_max=(main.get(i2).get(j2)-main.get(i1-1).get(j2)); } else if(j1!=0) { g_max=(main.get(i2).get(j2)-main.get(i2).get(j1-1)); } if(max<g_max) { max=g_max; } } } } } System.out.println("该二维数组整理区域和为:"+main); System.out.println("该二维数组最大块区域和为:"+max); } public static List<Integer> addList(List<Integer> a,List<Integer> b) { List<Integer> sum=new ArrayList<Integer>(); for(int i=0;i<a.size();i++) { sum.add(a.get(i)+b.get(i)); } // for(int i1=0;i1<a.size();i1++) // { // sum.set(i1,sum.get(i1)+b.get(i1)); // } return sum; } }
根据这个二维数组:

结果如下所示: