昨天提供的多项式函数模拟已经能够模拟绝大部分的曲线函数了,但是对于幂函数还有指数函数还是无能为力,我在网上找了很多的规律题,小学的规律题通过昨天的数列找规律算法基本都能模拟出正确答案,但是对于公务员的规律题,多项式的曲线函数模拟基本上很少能够模拟成功的。
今天欲通过添加指数和幂函数的方式,来让规律寻找算法编程一个更加普遍的形式。
scipy.optimize为我们提供了一个curve_fit的适应函数
我们构造一种普遍形式
ae^bx+cx^d+ex^fx+g的公式,来表示绝大部分的曲线,具有周期性的函数还不能表示
然后编写出以下更一般的曲线拟合函数代码:
import numpy as np from scipy.optimize import curve_fit import scipy.stats as stats def func_exxaxx(x,a,b,c,d,e,f,g): x=np.array(x) y = a*np.exp(b*x)+c*x**d+e*x**(f*x)+g return y def func_exxa(x,a,b,c,d,g): x=np.array(x) y = a*np.exp(b*x)+c*x**d+g return y def func_exxx(x,a,b,e,f,g): x=np.array(x) y = a*np.exp(b*x)+e*x**(f*x)+g return y def func_xaxx(x,c,d,e,f,g): x=np.array(x) y = c*x**d+e*x**(f*x)+g return y def func_ex(x,a,b,g): x=np.array(x) y = a*np.exp(b*x)+g return y def func_xa(x,c,d,g): x=np.array(x) y = c*x**d+g return y def func_xx(x,e,f,g): x=np.array(x) y =e*x**(f*x)+g return y allfunc=[func_exxaxx,func_exxa,func_exxx,func_xaxx,func_ex,func_xa,func_xx] def polyfit(x, y,limitfunc=lambda x:x**3): fit_coef_list, pcov_list=[],[] maxnh=0 id=0 suit=0 suiti=0 for i,one in enumerate(allfunc): try: fit_coef, pcov = curve_fit(one, x, y,maxfev=1500000) fit_coef_list.append(fit_coef) pcov_list.append(pcov) result=one([x],*fit_coef)[0] finalone=one([len(x)+1],*fit_coef)[0] downs=0.5 if abs(finalone-result[-1])>limitfunc(max(result)-min(result)) else 0 a,b=stats.pearsonr(result, y) score=a*(1-b)-downs print(one,score) id+=1 if(score>maxnh): maxnh=score suit=id-1 suiti=i except Exception: pass print(allfunc[suiti]) #参数 return fit_coef_list[suit],allfunc[suiti] def find_logical(y,limitfunc=lambda x:x**3): x_None=[] x=[] y_temp=[] for i,info in enumerate(y): if(info!=None): x.append(i+1) y_temp.append(info) else: x_None.append(i) fit_coef,func = polyfit(x, y_temp,limitfunc) for one in x_None: x.insert(one,None) return fit_coef,x,func
接着用两个实例来测试曲线拟合和数列寻找的效果,
还是前天曲线拟合的那些训练集:
y=2x^3+x^2+1
接下来分别取x=[1,2,3,4,5]
对应的y就为y=[4,21,64,145,276]
然后我们来预测x=6时y对应的值
#函数对应
y=[4,21,64,145,276]
x=list(range(1,len(y)+1,1))
fit_coef,func = polyfit(x, y)
print(func([6],*fit_coef))
结果如下
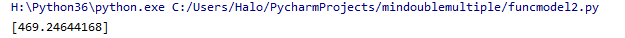
可以看到得到的结果是469.24 而正确的结果469
接着我们随便想一个有规律的数列,数列中包含有5个数
[11,111,1111,11111,111111]
接着将这个数列代入对应的数列规律寻找算法中,看看第6个数是什么
#数列规律(数学归纳法找第六位是什么) fit_coef,x,func=find_logical([11,111,1111,11111,111111]) print(func([6],*fit_coef))
测试结果
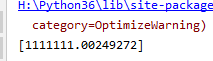
可以看到测试结果是1111111.002,而我们知道数列的下一个数是1111111,基本一致
接着提供斐波那契数列的前N项
[1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765]
我们来预测下一项是什么,经过计算 下一项应该是10946
#数列规律寻找下一项 fit_coef,x,func=find_logical([1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765]) print(func([len(x)+1],*fit_coef))
测试结果:
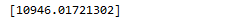
一致