最左下角开始找,一个数右边的数比当前数大,上边的数比当前数小,目标数比当前数大上移,比当前数小就右移
[ [1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30] ]
查找5,5比18小上移,5比10小上移,5比3大右移,5比6小上移,找到5
53 - II. 0~n-1中缺失的数字
mid>right,最小值一定在mid的右边,left=mid+1
mid<right,最小值一定是mid,或在mid的左边,right=mid
mid=left或mid=right,从right开始往左找最小值
50. 第一个只出现一次的字符
用LinkedHashMap
32.III. 从上到下打印二叉树 III
26. 树的子结构
前序遍历
A和B的根节点相同的话直接进入比较 isSubStructureDfs(A,B) A和B的根节点不相同看B是不是A的左子树或右子树的子结构 isSubStructure(A.left,B) || isSubStructure(A.right,B) 3 / 4 5 / 1 2 4 / 1 1、isSub(3,4) 3不等于4 返回false,看B是不是A的左子树的子结构 isSub(3的左子树,4) 2、isSub(4,4),dfs(4,4),4等于4,进行下一层递归 dfs(4的左子树,4的左子树),即dfs(1,1),1等于1,进行下一层递归 dfs(1的左子树,1的左子树),即dfs(null,null),B等于null返回true,进行下一层递归 dfs(1的右子树,1的右子树),即dfs(null,null),B等于null返回true,isSub(4,4)这个递归返回true结束递归
10- I. 斐波那契数列
数组的长度要n+1,因为有第0项
dp[i]=dp[i-1]+dp[i-2]
63. 股票的最大利润
第i天最大利润=max(前i-1天的最大利润,当天价格-前i-1天的最低价格)
前i-1天的最大利润的利润只用一个变量maxProfit维护,不用数组
当天价格-前i-1天的最低价格大于maxProfit就更新maxProfit
前i-1天的最低价格只用一个变量minPrice维护,不用数组:
当天价格小于minPrice就更新minPrice
42. 连续子数组的最大和
以每个位置为终点的和最大子数组 都是基于其前一位置的和最大子数组计算得出
转移方程: 若 dp[i-1] ≤0 ,说明 dp[i - 1]对 dp[i] 产生负贡献,即 dp[i-1] + nums[i]不如 nums[i] 本身大。
当 dp[i - 1] > 0 时:执行 dp[i] = dp[i-1] + nums[i] ;
当 dp[i - 1] ≤0 时:执行 dp[i] = nums[i] ;
47. 礼物的最大价值
i=0,j !=0,dp[i][j]=grid[i][j]+dp[i][j-1] i != 0,j = 0,dp[i][j]=grid[i][j]+dp[i-1][j] i != 0,j != 0,dp[i][j]=grid[i][j]+ max.(dp[i][j-1],dp[i-1][j])
dp*[*j] 代表以字符 s[j] 为结尾的 “最长不重复子字符串” 的长度
当 i < 0 ,即 s[j] 左边无相同字符,则 dp[j] = dp[j-1] + 1 ;
当 dp[j - 1] < j - i ,说明字符 s[j] 在子字符串 dp[j-1]dp[j−1] 区间之外 ,则 dp[j] = dp[j - 1] + 1 ;
当 dp[j - 1] ≥j−i ,说明字符 s[i] 在子字符串 dp[j-1]区间之中 ,则 dp[j] 的左边界由 s[i] 决定,即 dp[j] = j - i;
哈希表法:用哈希表记录字符所在的索引
线性遍历:左边界 i获取方式: 遍历到 s[j]时,初始化索引 i = j - 1,向左遍历搜索第一个满足 s[i] = s[j] 的字符即可
滑动窗口法
哈希表 dic统计: 指针 j遍历字符 s,哈希表统计字符 s[j]s[j] 最后一次出现的索引 。
更新左指针 i : 根据上轮左指针 i 和 dic[s[j]] ,每轮更新左边界 i,保证区间 [i + 1, j][i+1,j] 内无重复字符且最大。
i=max(dic[s[j]],i)
更新结果 res: 取上轮 res 和本轮双指针区间 [i + 1,j]的宽度(即 j - i)中的最大值。
res=max(res,j−i)
18.删除链表的节点
双指针法或dummy节点
初始化双指针法头结点是pre,头结点的next节点是cur
22.链表中倒数第k个节点
用双指针法不用统计数组长度
快指针先走k步,走完后快指针和慢指针相差k步,
然后慢指针和快指针一起走直到快指针为空就到达倒数第k个节点
5.合并两个排序的链表
用dummy节点
21. 调整数组顺序使奇数位于偶数前面
初始化left指针为0,right指针为nums.length-1
left指针指的一定是奇数,right指针指的一定是偶数
58 - I. 翻转单词顺序
从尾开始往前找每个单词
36. 二叉搜索树与双向链表
中序遍历构建双向链表
当 pre 为空时: 代表正在访问链表头节点,记为 head ;
中序遍历完成后要头指向尾,尾指向头形成循环链表
头指向尾:head.left = pre
尾指向头:pre.right = head
54. 二叉搜索树的第k大节点
反中序遍历右根左,第一个节点遍历的节点为第一大,第k个节点遍历的节点为第k大
40.最小的k个数
快排或大根堆
// 保持堆的大小为K,然后遍历数组中的数字,遍历的时候做如下判断: // 1. 若目前堆的大小小于K,将当前数字放入堆中。
// 2. 否则判断当前数字与大根堆堆顶元素的大小关系,如果当前数字比大根堆堆顶还大,这个数就直接跳过;
// 反之如果当前数字比大根堆堆顶小,先poll掉堆顶,再将该数字放入堆中。
64.求1+2+…+n
短路效应:(n > 1)|| sum(n-1) >0,n-1为false时,后面的递归会终止
7.重建二叉树
根据先序遍历索引构建根节点,根据根节点去中序遍历获取索引i用于划分左右子树
左子树:(先序遍历索引+1,左边界,索引i - 1)
右子树:(根节点索引+左子树数量+1,索引i +1,右边界)
根节点+左子树数量:左子树数量等于左子树右边界-左边界+1,即索引i - 1-左边界+1,要加1才是数量
不过递归地找出当前子树的根节点和这个节点的左右子树
前序遍历:[3,9,20,15,7],中序遍历:【9,3,15,20,7】
根据先序遍历索引0构建根节点3,根据根节点3去中序遍历获取索引1,(0,0)是左子树,(2,4)是右子树
递归处理左子树和右子树
左子树:(0+1,0,0),递归构建的左子树根节点要返回作为上一层递归的根节点的左子树
右子树:(0+0-0+1+1,2,4),递归构建的右子树根节点要返回作为上一层递归的根节点的右子树
15.二进制中1的个数
拿1作为掩码,和原数每一个进行与运算,如果位数为1的结果是1,不是的话结果为0,从右往左与
33.二叉搜索树的后序遍历序列
数组最后一个是根节点,然后从左往右找第一个比根节点大的数,然后这个数后面的数都比根节点大,然后递归处理左右子树,左子树:left,i-1 右子树:i,right-1
[1,3,2,6,5]
根节点为5,找到第一个比根节点大的数6,再递归处理左子树:【1,3,2】,右子树:【6】
65. 不用加减乘除做加法
先异或得到无进位的和sum,然后与运算左移后得到进位carry后,这两个数相加,因为不能用加法所以实现这两个数相加要接着算不进位求和加上进位的值,再计算新的进位,依次重复下去,直到进位为 0 为止
相同的数异或是0,因为异或是半加法
^得到的是一个无进位的加法 这个结果可能要比a和b本身还小 比如18+3本来是21 但是异或后得到的是17 为什么呢?18:10010 3:00011 异或后:10001=17可以看到本来第二个1那个地方该进位的,异或后不仅没有进位,反而变成了0 这就相当于少加了00100这个数,那如何能得到这个数呢?使用&因为只有两个位都是1了才会进位,刚好对应两个1异或后消失的那个进位,但是&后需要左移一下才能模拟那个数。
56 - I. 数组中数字出现的次数
先对数组进行异或,得到的结果是x和y的异或,然后找出x,y的最低不同位,最后根据这位去对数组进行与运算分成两组,分成两组后就可以分别对这两组进行异或找出两个只出现一次的数字
假设数组异或的二进制结果为10010,那么说明这两个数从右向左数第2位是不同的
那么可以根据数组里面所有数的第二位为0或者1将数组划分为2个。
数组【1,2,5,2】异或后得到0100,从右往左找到第三位是1,也就是x,y从第三位开始不同,然后根据这位分成两组:【1,2,2】,【5】,再分别对这两组进行异或得到1,5就是x,y
56 - II. 数组中数字出现的次数 II
int count[] = new int[32]; for (int num : nums) { //从最低位开始统计1的数量 for (int i = 0; i < 32; i++) { count[i] += num & 1; num >>= 1; } } int res = 0; //从最高位开始恢复 for (int i = 31; i >= 0; i--) { res <<= 1; res |= count[i]%3; } return res;
66. 构建乘积数组
算出数组每个数左边的乘积和右边的乘积
14- I. 剪绳子
剪了第一段后,剩下(i - j)长度可以剪也可以不剪。如果不剪的话长度乘积即为j * (i - j);如果剪的话长度乘积即为j * dp[i - j]。取两者最大值max(j * (i - j), j * dp[i - j]) 第一段长度j可以取的区间为[2,i),对所有j不同的情况取最大值,因此最终dp[i]的转移方程为 dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j])) i是总长度,j是减掉的长度 忽略dp[1]是因为长度为1减不了 用乘是因为求的最大乘积
14.剪绳子2.0
我们首先考虑对于一段长n的绳子,我们可以切出的结果包含什么?
1会包含吗? 不会,因为1 * (k - 1) < k, 只要把1和任何一个其他的片段组合在一起就有个更大的值
2可以
3可以
4可以吗? 它拆成两个2的效果和本身一样,因此也不考虑
5以上可以吗? 不可以,这些绳子必须拆,因为总有一种拆法比不拆更优,比如拆成 k / 2 和 k - k / 2
综上, 最后的结果只包含2和3(当然当总长度为2和3时单独处理), 那么很显然n >= 5时, 3*(n - 3) >= 2 * (n - 2) ,因此我们优先拆成3,最后剩余的拆成2。最后的结果一定是由若干个3和1或2个2组成.
切剩2或3或4就不用再切,因为不切比切要好
57 - II. 和为s的连续正数序列
比target大就left指针右移(缩小窗口),比target小就right指针右移(扩大窗口)
62.圆圈中最后剩下的数字(参考力扣题解:https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/solution/huan-ge-jiao-du-ju-li-jie-jue-yue-se-fu-huan-by-as/,作者:aspenstars)
F(n,m)表示最后剩下那个人的索引号
从N = 7 到N = 8 的过程
如何才能将N = 7 的排列变回到N = 8 呢?
我们先把被杀掉的C补充回来,然后右移m个人,发现溢出了,再把溢出的补充在最前面
神奇了 经过这个操作就恢复了N = 8 的排列了!
因为N=8时D前面有3个数,7变成8时要补回这3个数,采用的方法是右移3位然后求余

因此我们可以推出递推公式f(8,3) = [f(7, 3) + 3] \% 8f(8,3)=[f(7,3)+3]%8
进行推广泛化,即f(n,m) = [f(n-1, m) + m] \% nf(n,m)=[f(n−1,m)+m]%n
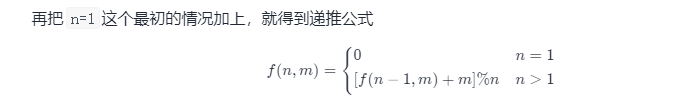
38. 字符串的排列
List<String> list2 = new ArrayList<>();
public String[] permutation(String s) {
int length = s.length();
if (length == 0) {
return new String[0];
}
char[] chars = s.toCharArray();
Arrays.sort(chars);
StringBuffer path = new StringBuffer();
//判断字符有没被访问
boolean[] used = new boolean[length];
permutationDfs(path,chars,0,used,length);
return list2.toArray(new String[0]);
}
int count = 0;
public void permutationDfs(StringBuffer path, char[] chars, int index, boolean[] used, int length) {
//得到一个结果
if (index == length) {
list2.add(path.toString());
return;
}
for (int i = 0; i < length; i++) {
//当前字符还没访问过
count++;
if (!used[i]) {
//剪枝处理同层重复元素,chars[i] == chars[i-1]为了防止重复读取,例如aab,读了第一个a,第二a就不读
// used[i - 1] == true,说明同一树支nums[i - 1]使用过
// used[i - 1] == false,说明同一树层nums[i - 1]使用过
// 如果同一树层nums[i - 1]使用过则直接跳过
if (i > 0 && chars[i] == chars[i-1] && !used[i-1]) {
continue;
}
used[i] = true;
//做选择
path.append(chars[i]);
permutationDfs(path,chars,index+1,used,length);
//撤销选择
path.deleteCharAt(path.length()-1);
used[i] = false;
}
}
}
回溯法,用一个数组判断当前字符是否被访问过
保证在填每一个空位的时候重复字符只会被填入一次,在递归函数中,我们限制每次填入的字符一定是这个字符所在重复字符集合中「从左往右第一个未被填入的字符」
!used[i-1]的作用是前一个树层访问完了,前一个树层访问完了会撤销选择把visited【i-1】标为false

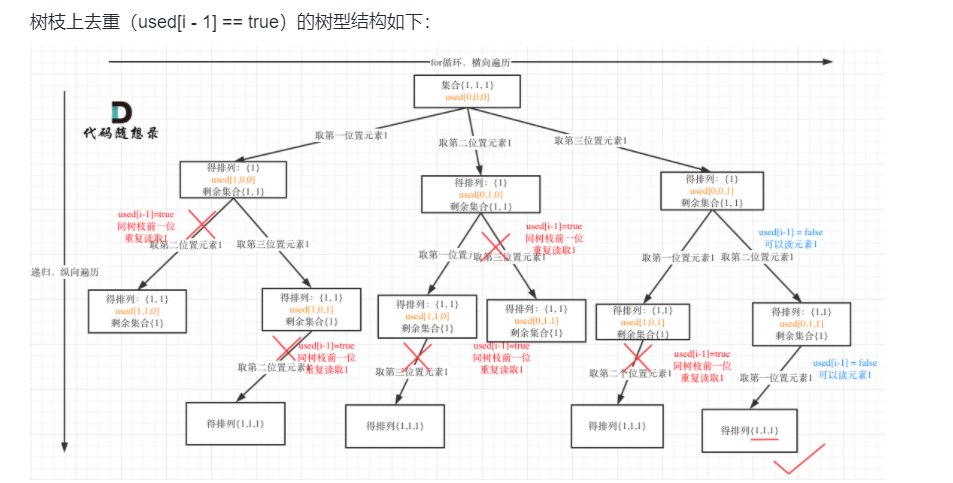
树枝是一个节点,树层是几个节点,used[i - 1] == false说明前一个树层递归完了撤销选择把used[i - 1] 恢复为false,所以 used[i - 1] == false代表前一个树层访问过了和当前树层是重复的然后就剪枝,剪树层剪了几个节点,剪树枝只是剪了一个节点
59 - II. 队列的最大值
用两个队列,一个普通队列,一个单调队列,单调队列的对头是队列的最大值,如果普通队列的对头刚好是队列的最大值,出队时单调队列的对头元素也要出队
12 - I矩阵中的运动路径
- 使用二维布尔数组记录之前的位置是否已经被访问过,如果已经被访问过的话,则在 dfs 的过程中,直接 return false 即可。也就是说,此路已经不通了;
- 如果当前遍历到的字符不等于 board[i][j] 位置上的字符,那么说明此路也是不通的,因此返回 false;
- 至于递归结束的条件:如果指针 start 能够来到 word 的最后一个字符,那么说明能够在矩阵 board 中找到一条路径,此时返回 true;
- 在遍历到当前 board[i][j] 的时候,首先应将该位置的 visited[i][j] 设置为 true,表明访问过;
- 然后,递归地去 board[i][j] 的上下左右四个方向去找,剩下的路径;
- 在 dfs 的过程当中,如果某条路已经不通了,那么那么需要回溯,也就是将 visited[i][j] 位置的布尔值重新赋值为 fasle;
- 最后,返回 ans 即可
49 丑数
nums2 = {1*2, 2*2, 3*2, 4*2, 5*2, 6*2, 8*2...}
nums3 = {1*3, 2*3, 3*3, 4*3, 5*3, 6*3, 8*3...}
nums5 = {1*5, 2*5, 3*5, 4*5, 5*5, 6*5, 8*5...}
把这三个数组排序,然后取第n个
例如一开始a=0,b=0,c=0,dp【0】=1
dp[1]=min(dp[a]*2,dp[b]*3,dp[c]*5)=min(dp[0]*2,dp[0]*3,dp[0]*5);
dp[a]*2是最小的
所以第二个丑数是dp【a】*2即2,dp【a】*2用完了,即比较完了后面再无需比较,然后a指针右移一位,
dp[2]=min(dp[a]*2,dp[b]*3,dp[c]*5)=min(dp[1]*2,dp[0]*3,dp[0]*5);
dp[b]*3是最小的
所以第三个丑数是dp【b】*3即3,dp[b]*3用完了,即比较完了后面再无需比较,然后b指针右移一位
以此类推算到第n个丑数
使用当前丑数是否等于前一个丑数*2或3或5来判断哪个指针右移,例如第二个丑数等于第一个丑数乘2,a指针右移,第三个丑数等于第二个丑数乘3,b指针右移
29. 顺时针打印矩阵
设定四个边界,上下左右
依次打印:左到右,上到下,右到左,下到上
左边界小于右边界和上边界小于下边界时可以打印右到左和上到下
打印完一层向内层收缩,上边界和左边界加1,下边界和右边界减1,直到收缩到最后一层,最后一层打印完是左边界大于右边界,上边界大于下边界
60.n个骰子的点数
n个骰子,一共有6**n种情况
f(n, s) 表示n个骰子点数的和为s的排列情况总数
n=1, 和为s的情况有 F(n,s)=1 s=1,2,3,4,5,6
n>1 , F(n,s) = F(n-1,s-1)+F(n-1,s-2) +F(n-1,s-3)+F(n-1,s-4)+F(n-1,s-5)+F(n-1,s-6)
s-1 s要大于1
s-2 s要大于2,
s-3 s要大于3,
s-4 s要大于4,
s-5 s要大于5,
s-6 s要大于6,
dp[2][2]表示2个骰子点数的和为2出现了多少次
dp[2][2]=dp[1][1],dp[1][1]为1,所以dp【2】【2】为1
dp[1][1]+骰子点数为1就等于dp[2][2],因为1个骰子点数的和为1出现的次数再加上一个骰子点数为1刚好就凑成了2个骰子点数的和为2出现的次数
int[][] dp = new int[n+1][6*n+1]; double[] res = new double[5*n+1]; double pow = Math.pow(6,n); for (int i = 1; i < 7; i++) { dp[1][i] = 1; } //i是骰子数,j是出现的点数,k是拿来凑的数 for (int i = 2; i <= n; i++) { for (int j = i; j <= 6*i; j++) { for (int k = 1; k <= 6; k++){ //要大于0是因为如果求dp[2][2]只能由dp[1][1]得出,不能由dp[1][2]得出 if (j - k > 0) { dp[i][j] += dp[i-1][j-k]; } else { break; } } } } for (int i = n; i <= 6*n; i++) { // i 的最小值为 n,在 res 里是第 i - n 位 res[i - n] = dp[n][i]/pow; } return res;
16.数组的整次数方
偶数: 计算Power(3,8),我们可以改为Power(3*3,8/2) 奇数: Power(3,9),我们只需要计算3*Power(3*3,9/2),也就是3*Power(9,4) n是负数: Power(3,-8),改成Power(1/3,8) Power(3,-2147483648),要改成1/3*Power(1/3,-(-2147483648+1))
因为-2147483648直接取反还是自己,因为32位的最大正数为2147483647,在加1就溢出变成了-2147483648,所以-2147483648直接取反还是自己
45.把数组排成最小的数
首先我们要明白就是
无论这些数字怎么取排列,形成的数字的位数是不变的
那么就是高位的数字肯定是越小越好。
我们先考虑一下怎么排列两个数字,比如 1 和 20,高位越小越好,放 1,组合成 120
把数字转换成字符串再从左往右比较每一个数字
36、38 和 5,首先肯定先放 36,剩下 38 和 5,然后对这两个数进行排列 385,所以最后的结果为 36385
3和30,330>303,所以3<30
若拼接字符串 x + y > y + x ,则 x “大于” y;
反之,若 x + y < y + x ,则 x“小于” y ;
例如x为31,y为32,3132<3231,则31<32,因为从左往右比第一位3相同,就比第二位,第2位1比2小,所以就31<32
51.数组中的逆序对
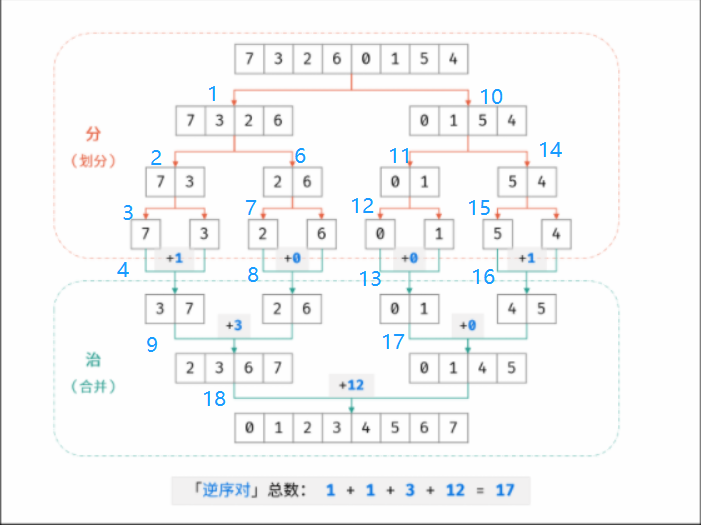
先把数组分隔成子数组,统计出子数组内的逆序对的数目,然后再统计出两个相邻子数组之间的逆序对的数目,统计完子数组内的逆序对的数目后要对子数组排序,排序完之后再统计出两个相邻子数组之间的逆序对的数目
7,5,6,4
子数组7,5 6,4
这两个子数组有两个逆序对
统计完这两个子数组后对这两个子数组进行排序,然后统计出两个相邻子数组之间的逆序对的数目,只能是第一个数组和第二数组比,因为是逆序对只能是前面和后面的比
5,7 4,6
7比6大,子数组大小为2,6是最大的,所以7增加两个逆序对
5比6小没有逆序对
5比4大,5增加一个逆序对
总逆序对是2+2+1
第一张图是遍历顺序
第二张图为每轮递归时l和r的值,类似于二叉树的后序遍历,l等于r时数组只剩一个元素,相当于叶子节点
第三张图为后序遍历完返回 l和r的值,合并排序之前的数组和合并排序之后的数组,排序完之后l和r之间的数组都是有序的
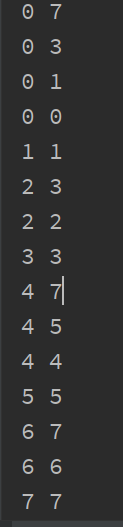

转成二叉树是
0
/
0 0
/ /
0 0 0 0
/ / / /
7 3 2 6 0 1 5 4
l:0 r:0返回 l:1 r:1返回 上一层递归l为0,为1
发生相等情况时,都默认移动左边的
int[] nums, tmp; public int reversePairs(int[] nums) { this.nums = nums; tmp = new int[nums.length]; return mergeSort(0,nums.length-1); } private int mergeSort(int l, int r) { //递归终止条件 if (l >= r) { return 0; } //递归划分边界 int m = (l + r)/2; //开始递归 int res = mergeSort(l,m) + mergeSort(m+1,r); //合并阶段 int i = l;//第一个子数组的指针 int j = m+1;//第二个子数组的指针 //将[l,r]用一个数组保存合并之前的模样 for (int k = l; k <= r; k++) { tmp[k] = nums[k]; } for (int k = l; k <= r; k++) { //m及其左边元素合并完毕,即第一个子数组合并完毕,把右边剩下的放入合并后的数组,合并的步骤 if (i == m+1) { nums[k] = tmp[j++]; j++; //m+1及其右边元素合并完毕,即第二个子数组合并完毕,把左边剩下的放入合并后的数组 //或者 左边数组的元素小于等于右边,将左边数组的元素放入结果数组中,并让指针i加1,合并的步骤 } else if (j == r+1 || tmp[i] <= tmp[j]) { nums[k] = tmp[i++]; i++; //统计逆序对 } else if (tmp[i] > tmp [j]) { //第二个子数组的当前数已经和第一个子数组比较完了,指针右移,合并的步骤 nums[k] = tmp[j]; //只要第二个子数组的当前数比第一个子数组的当前数小,第二个子数组的当前数都比第一个子数组的当前数的右边所有数小 res += m - i + 1; j++; } } return res; }