3647 [APIO2014]连珠线
题目描述
在达芬奇时代,有一个流行的儿童游戏称为连珠线。当然,这个游戏是关于珠子和线的。线是红色或蓝色的,珠子被编号为 1 到 n。这个游戏从一个珠子开始,每次会用如下方式添加一个新的珠子:
Append(w, v):一个新的珠子 $w$ 和一个已经添加的珠子 v 用红线连接起来。
Insert(w, u, v):一个新的珠子$w$插入到用红线连起来的两个珠子$u,v$之间。具体过程是删去 u,v 之间红线,分别用蓝线连接 u,w 和 w, v。
每条线都有一个长度。游戏结束后,你的最终得分为蓝线长度之和。
给你连珠线游戏结束后的游戏局面,只告诉了你珠子和链的连接方式以及每条线的长度,没有告诉你每条线分别是什么颜色。
你需要写一个程序来找出最大可能得分。即,在所有以给出的最终局面结束的连珠线游戏中找出那个得分最大的,然后输出最大可能得分。
输入格式
第一行一个正整数 $n$,表示珠子的数量。珠子从 1 到 n 编号。
接下来 n - 1 行每行三个整数 $a_{i},b_{i},c_{i}$。保证 $1 leqslant a_{i},b_{i} leqslant n$,$1 leqslant c_{i} leqslant 10000$。表示 ai 号珠子和 bi 号珠子间连了长度为 ci 的线。
输出格式
输出一个整数,表示最大可能得分。
输入输出样例
5 1 2 10 1 3 40 1 4 15 1 5 20
140
说明/提示
【样例描述1】
可以通过如下方式获得 60 分:首先从 3 号珠子开始。
把 5 和 3 连起来。(线长度任意)
在 3 和 5 之间插入 $11$。(线长分别为 40 和 20)。
把 2 和 1 用长度为 $10$ 的线连起来。
把 4 和 1 用长度为 $15$ 的线连起来。
【限制与约定】
第一个子任务共 13 分,满足 $1leqslant n leqslant 10$
第二个子任务共 15 分,满足 $1leqslant n leqslant 200$
第三个子任务共 29 分,满足 $1leqslant n leqslant 10000$
第四个子任务共 43 分,满足 $1leqslant n leqslant 200000$
Solution:
为了方便,我们把每个珠子看成一个节点
我们非常开心的发现,结果肯定是一棵边颜色不同的树
由于刚开始只有任意的一个节点,就相当于我们选择一个节点为根,
然后进行两种操作:
1.每次扩展一个节点的儿子,即把一个节点和已经在树上的一个点连上一条红边,且不在这两个点之间加珠子:
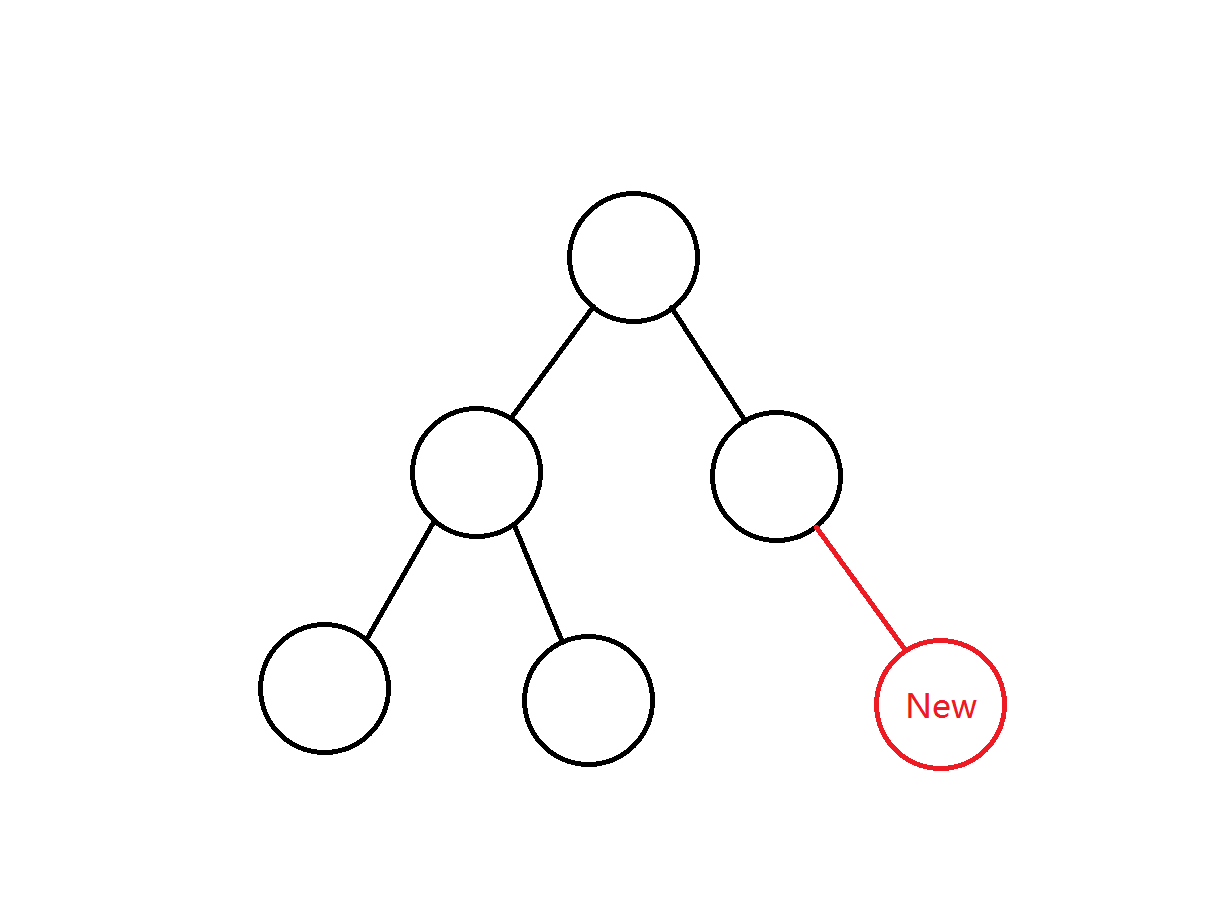
或者扩展一个节点的孙子再扩展这个孙子的爸爸,就是把树上的一个节点连到另一个节点上,在把一个节点插到这两个节点之间,把两条边染成蓝色,即:
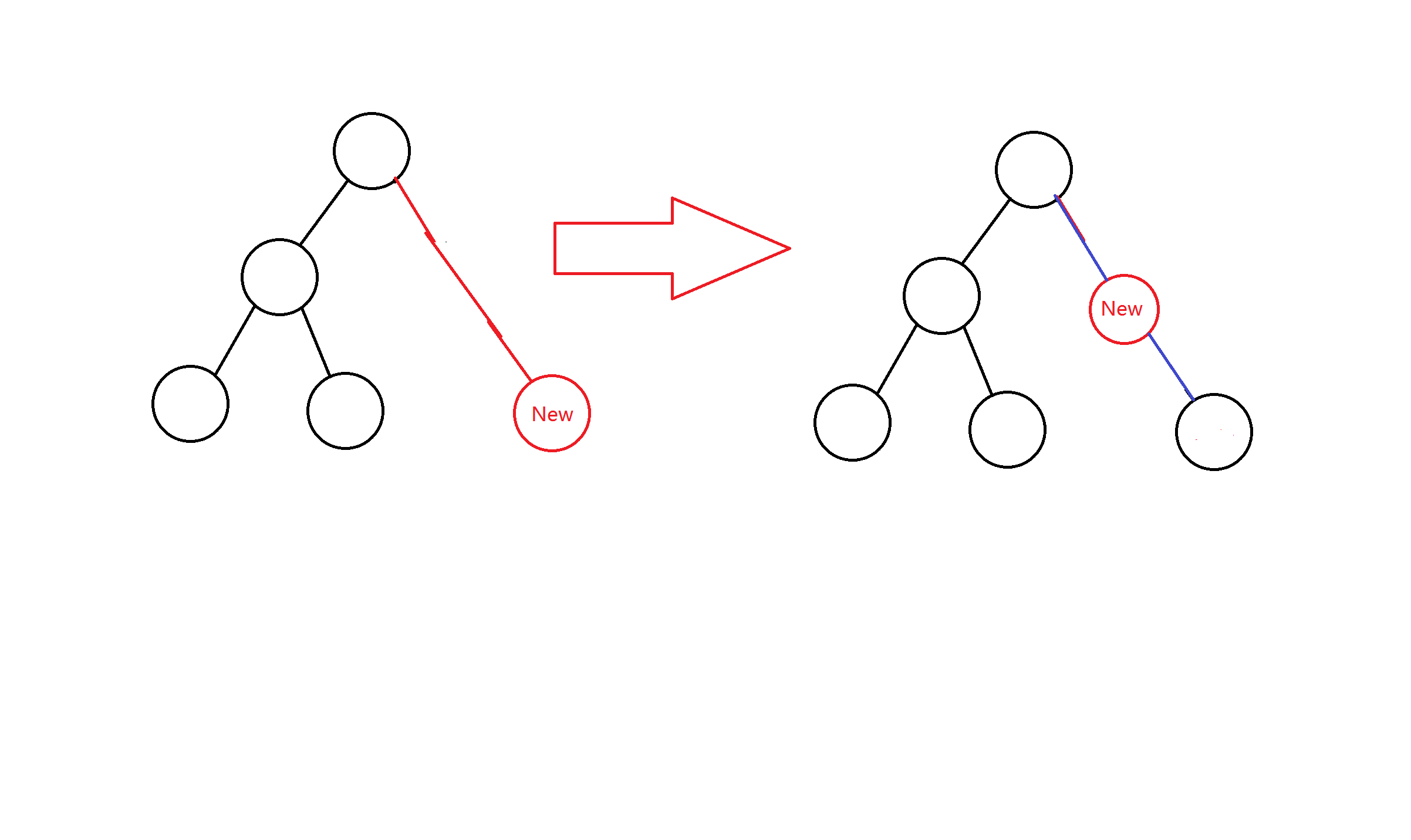

PS:如果出现一个根为蓝线的中点,那么它不可能是第一个出现的珠子
好的,假设以1号点为根,我们可以列出一个DP方程式
f[i][0/1]表示当前节点是否为中点获得的最大价值
$f[i][0]=sumlimits_{j}^{j in son[i]}max(f[j][0],f[j][1]+dis(i,j));$
$f[i][1]=f[i][0]+max(f[j][0]-max(f[j][0],f[j][1]+dis(i,j)));(j in son[i])$
为了进行换根DP,我们设$g[i][j][0/1](j in son[i])$表示f[i][0/1]不考虑儿子j的贡献所能获得的最大贡献
也不难求,即:
$g[i][j][0](j in son[i])=f[i][0]-max(f[j][0],f[j][1]+dis(i,j))$
$g[i][j][1]$同理,记录一下最大值和次大值即可
然后我们需要换根进行DP
对于每一个儿子,我们实际上将它的父亲当做它的儿子,为它提供贡献即可,这个东西还是直接看代码好懂一点的吧
void dp2(int x,int y){ if(!son[x].size()) return; if(son[x].size())rep(i,0,son[x].size()-1){ f[x][0]=g[x][0][i]; f[x][1]=g[x][1][i]; if(fa[x]){ f[x][0]+=max(f[fa[x]][0],f[fa[x]][1]+y); f[x][1]=f[x][0]+max(maxxx[x][i],-max(f[fa[x]][0],f[fa[x]][1]+y)+f[fa[x]][0]+y); } ans=max(ans,f[son[x][i]][0]+max(f[x][0],f[x][1]+len[x][i])); dp2(son[x][i],len[x][i]);//由于是dfs的进行Dp,所以f[fa[x]][0/1]表示的就是以fa[x]为根的最大价值,故可以这样直接转移 } }
完结撒花o((>ω< ))o
CODE:
#include<iostream> #include<algorithm> #include<cstring> #include<cstdio> #include<vector> #define rep(i,a,b) for(int i=a;i<=(b);i++) #define int long long #define MAXN 200040 using namespace std; int n,to[MAXN<<1],nxt[MAXN<<1],fir[MAXN],val[MAXN<<1],tot,f[MAXN][2],ans,fa[MAXN]; vector<int> son[MAXN],len[MAXN],g[MAXN][2],maxxx[MAXN]; void ade(int x,int y,int z){ to[++tot]=y; nxt[tot]=fir[x]; fir[x]=tot; val[tot]=z; } void dp1(int x,int y){ fa[x]=y; int maxx1=-888888888,maxx2=-888888888; for(int k=fir[x];k;k=nxt[k]){ if(to[k]==y) continue; son[x].push_back(to[k]); dp1(to[k],x); f[x][0]+=max(f[to[k]][0],f[to[k]][1]+val[k]); len[x].push_back(val[k]); if(maxx1<-max(f[to[k]][0],f[to[k]][1]+val[k])+f[to[k]][0]+val[k]) maxx2=maxx1,maxx1=-max(f[to[k]][0],f[to[k]][1]+val[k])+f[to[k]][0]+val[k]; else if(maxx2<-max(f[to[k]][0],f[to[k]][1]+val[k])+f[to[k]][0]+val[k]) maxx2=-max(f[to[k]][0],f[to[k]][1]+val[k])+f[to[k]][0]+val[k]; } f[x][1]=f[x][0]+maxx1; if(!son[x].size()) return; rep(i,0,son[x].size()-1){ g[x][0].push_back(f[x][0]-max(f[son[x][i]][0],f[son[x][i]][1]+len[x][i])); int tmp=-max(f[son[x][i]][0],f[son[x][i]][1]+len[x][i])+f[son[x][i]][0]+len[x][i]; if(tmp==maxx1) g[x][1].push_back(g[x][0].back()+maxx2),maxxx[x].push_back(maxx2); else g[x][1].push_back(g[x][0].back()+maxx1),maxxx[x].push_back(maxx1); } } void dp2(int x,int y){ if(!son[x].size()) return; if(son[x].size())rep(i,0,son[x].size()-1){ f[x][0]=g[x][0][i]; f[x][1]=g[x][1][i]; if(fa[x]){ f[x][0]+=max(f[fa[x]][0],f[fa[x]][1]+y); f[x][1]=f[x][0]+max(maxxx[x][i],-max(f[fa[x]][0],f[fa[x]][1]+y)+f[fa[x]][0]+y); } ans=max(ans,f[son[x][i]][0]+max(f[x][0],f[x][1]+len[x][i])); dp2(son[x][i],len[x][i]); } } main(){ scanf("%lld",&n); rep(i,1,n-1){ int x,y,z; scanf("%lld%lld%lld",&x,&y,&z); ade(x,y,z); ade(y,x,z); } dp1(1,0); dp2(1,-88888888); cout<<ans; return 0; }