奇妙的算法之LCS妙解

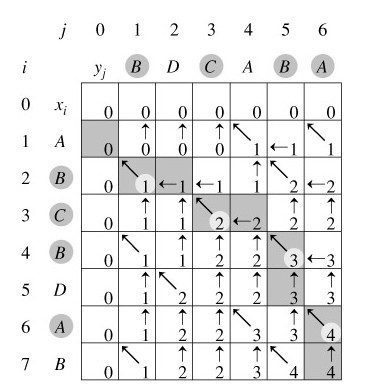
                                                                      LCS算法妙解

LCS问题简述：最长公共子序列

一个数列 S，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则S 称为已知序列的最长公共子序列。

LCS问题的分支：最长公共子串与最长公共子序列

子串（Substring）是串的一个连续的部分，子序列（Subsequence）则是从不改变序列的顺序，而从序列中去掉任意的元素而获得的新序列；更简略地说，前者（子串）的字符的位置必须连续，后者（子序列LCS）则不必。比如字符串acdfg同akdfc的最长公共子串为df，而他们的最长公共子序列是adf。

LCS解题策略：

one：穷举法。。。复杂度不再多说，想想2的N次方就感到可怕；

two：矩阵，也就是动态规划节LCS问题，也就是今天咱的标题；

下面来细讲the twith idea：

 由此图可以看出此经典算法的思路；

下面是代码，方便大家理解：

#include<stdio.h>
#include<string.h>
#define MAX(a,b) (a>b?a:b)
const int MAXN=1010;
int dp[MAXN][MAXN];
char a[MAXN],b[MAXN];
int main(){
while(~scanf("%s%s",a+1,b+1)){
    memset(dp,0,sizeof(dp));
    int i,j;
    for( i=1;a[i];i++){
        for(j=1;b[j];j++){
            if(a[i]==b[j])dp[i][j]=dp[i-1][j-1]+1;
            else dp[i][j]=MAX(dp[i][j-1],dp[i-1][j]);
        }
    }
    printf("%d
",dp[i-1][j-1]);
}
return 0;}

此递归关系为：

1. 若x_m=y_n，则z_k=x_m=y_n且Z_k-1是X_m-1和Y_n-1的最长公共子序列；
2. 若x_m≠y_n且z_k≠x_{m ，}则Z是X_m-1和Y的最长公共子序列；
3. 若x_m≠y_n且z_k≠y_n ，则Z是X和Y_n-1的最长公共子序列。

此算法时间复杂度为n*m，空间复杂度也是n*m;

另外若要记录路径就比较复杂了；

lcs解决lis问题：

需要先排序，然后与原数组求最长公共子序列；

下面是道题poj上的，就用到了此题的思想：

Common Subsequence

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 43194		Accepted: 17514

Description

A subsequence of a given sequence is the given sequence with some elements (possible none) left out. Given a sequence X = < x1, x2, ..., xm > another sequence Z = < z1, z2, ..., zk > is a subsequence of X if there exists a strictly increasing sequence < i1, i2, ..., ik > of indices of X such that for all j = 1,2,...,k, x_ij = zj. For example, Z = < a, b, f, c > is a subsequence of X = < a, b, c, f, b, c > with index sequence < 1, 2, 4, 6 >. Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y.

Input

The program input is from the std input. Each data set in the input contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct.

Output

For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.

Sample Input

abcfbc         abfcab
programming    contest 
abcd           mnp

Sample Output

4
2
0

还有南阳oj上面有道最长公共子序列更是LCS的模板；