洛谷P3884《[JLOI2009]二叉树问题》

原创建时间：2018-08-08 16:31:55

不用倍增的 almost裸的LCA

题目描述

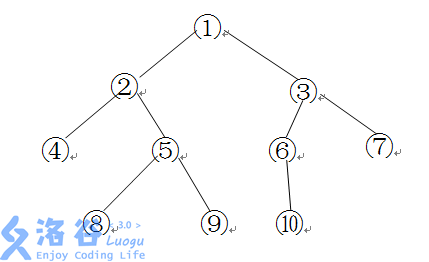
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

深度：4 宽度：4（同一层最多结点个数）

结点间距离： ⑧→⑥为8 (3×2+2=8)

⑥→⑦为3 （1×2+1=3）

注：结点间距离的定义：由结点向根方向（上行方向）时的边数×2，

与由根向叶结点方向（下行方向）时的边数之和。

图片来自洛谷

Input / Output 格式 & 样例

输入格式

输入文件第一行为一个整数n(1≤n≤100)，表示二叉树结点个数。接下来的n-1行，表示从结点x到结点y（约定根结点为1），最后一行两个整数u、v，表示求从结点u到结点v的距离。

输出格式：

三个数，每个数占一行，依次表示给定二叉树的深度、宽度及结点u到结点v间距离。

输入输出样例

输入样例：

10                                
1 2                            
1 3                            
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6

输出样例：

4
4
8

解题思路

树的深度可以取(max){(depth[i])}

树的宽度可以在取深度的时候拿一个桶记录下来，再循环取一遍(max)

两点之间的距离可以先求(LCA)，再用一个公式算出来

[distance = (depth[u] - depth[lca]) imes 2 + depth[v] - depth[lca] ]

其中(lca = LCA(u, v))

代码实现

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>
using namespace std;

const int MAXN = 100 + 10;

struct Edge {
    int prev, next;
} edge[MAXN * 2];

int head[MAXN], father[MAXN][22], lg[MAXN], depth[MAXN];
int cnt, n, m, s;
int KangShifu[MAXN];

inline int getint() {
    int s = 0, x = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-') x = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        s = s * 10 + ch - '0';
        ch = getchar();
    }
    return s * x;
}

inline void putint(int x, bool returnValue) {
    if (x < 0) {
        x = -x;
        putchar('-');
    }
    if (x >= 10) putint(x / 10, false);
    putchar(x % 10 + '0');
    if (returnValue) putchar('
');
}

inline void addEdge(int prev, int next) {
    edge[++cnt].prev = prev;
    edge[cnt].next = head[next];
    head[next] = cnt; 
} 

void dfsInit(int root, int fa) {
    depth[root] = depth[fa] + 1;
    father[root][0] = fa;
    for (int i = 1; (1 << i) <= depth[root]; ++i) {
        father[root][i] = father[father[root][i-1]][i-1];
    }
    for (int e = head[root]; e; e = edge[e].next) {
        if (edge[e].prev != fa) dfsInit(edge[e].prev, root);
    }
}

int LCA(int x, int y) {
    if (depth[x] < depth[y]) swap(x, y);
    while (depth[x] > depth[y]) 
        x = father[x][lg[depth[x] - depth[y]] - 1];
    if (x == y) return x;
    for (int i = lg[depth[x]]; i >= 0; --i) {
        if (father[x][i] != father[y][i]) x = father[x][i], y = father[y][i];
    }
    return father[x][0];
}

int main(int argc, char *const argv[]) {
    n = getint();
    for (int i = 1; i < n; ++i) {
        int prev = getint(), next = getint();
        addEdge(prev, next);
        addEdge(next, prev);
    } 
    int u = getint();
    int v = getint();
    dfsInit(1, 0);
    for (int i = 1; i <= n; ++i) {
    	lg[i] = lg[i-1] + (1 << lg[i-1] == i);
    }
    int lca = LCA(u, v);
    int Depth = -23333;
    for (int i = 1; i <= n; ++i) {
        Depth = std::max(Depth, depth[i]);
        ++KangShifu[depth[i]];
    }
    int width = -23333;
    for (int i = 1; i <= Depth + 2; ++i) width = std::max(width, KangShifu[i]);
    putint(Depth, true);
    putint(width, true);
    putint((depth[u] - depth[lca]) * 2 + (depth[v] - depth[lca]), true);
    return 0;
}