KMP的理解与模板

　　　　　　　　　　　　　　　　　　KMP

T串主串 P串模式串

i

T串：A  B  C  A  B  C  D  H  I  J  K

P串：      A  B  C  E

j

保持i指针不回溯，通过修改j指针，让模式串尽量地移动到有效的位置

接下来我们自己来发现j的移动规律：

 

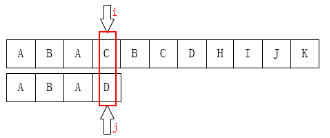
如图：C和D不匹配了，我们要把j移动到哪？显然是第1位。为什么？因为前面有一个A相同啊：

 

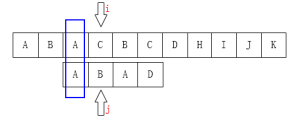
如下图也是一样的情况：

 

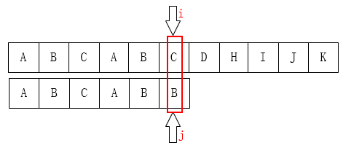
可以把j指针移动到第2位，因为前面有两个字母是一样的：

 

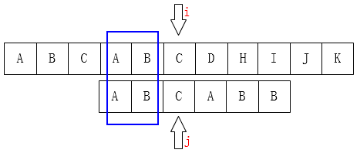
当匹配失败时，j要移动到下一个位置k。（模式串）存在着这样的性质：最前面的k个字符和j之前的最后k个字符是一样的。

P[0~k-1] ==P[j-k~j-1]

比如: a b c d a b c  
i == : 0 1 2 3 4 5 6  7
next:-1 0 0 0 0 1 2  3

初始化Next[]数组：

void get_next() //初始化next数组 lenp为p数组的长度

{

    int i,j;

Next[0] = j = -1;

 

    i = 0;

    while(i<lenp)  //最后一位的判断其实是多余的

    {

        while(j!=-1&&p[j]!=p[i])

            j = Next[j];

        Next[++i] = ++j;

    }

}

-----------------------------------------------------------------------------------------------------------------------

Kmp部分：

i：       0 1 2 3 4 5 6 7 8 9

T串：    a b c e a b p a b c

P串：    a b c d a b c

Next[]：  -1 0 0 0 0 1 2

当i=3处，j= 3 ，t[i]!=p[j],j的指针返回到next[3] 即 j = 0

i：       0 1 2 3 4 5 6 7 8 9

T串：    a b c d a b p a b c

P串：    a b c d a b c

Next[]：  -1 0 0 0 0 1 2

若一直匹配至i=6；

j= 6，t[i]!=p[j],j返回到next[6]  移动j指针 即j=2

int kmp1()  //在t串找p串  返回下标

{

    int i,j;

    i = j = 0; //两个下标指针 i为主串的指针 j为模式串的指针

    while(i<lent&&j<lenp)

    {

        while(j!=-1&&t[i]!=p[j])

            j = Next[j];

        i++;

        j++;

    }

    if(j==lenp)

        return i-j; //若找到返回开始下标（从0开始）

    return -1;   //找不到返回-1

}

 

t[]  aaaaaa

p[]  aa

返回的ans = 5

int kmp2() //返回匹配次数

{

    int i,j;

    i = j = 0;

    int ans = 0;

    while(i<lent)

    {

        while(j!=-1&&t[i]!=p[j])

            j = Next[j];

        if(j==lenp-1)

        {

            ans++;

            j = Next[j];

        }

        i++;

        j++;

    }

    return ans;

}

t[] aaaaaaa

p[] aaa

返回的ans = 2

int kmp3() //返回t串中有多少个p串

{

    int i,j;

    i = j = 0;

    int ans = 0;

    while(i<lent)

    {

        while(j!=-1&&t[i]!=p[j])

            j = Next[j];

        if(j==lenp-1)

        {

            ans++;

            j = -1;    // j指针改变为-1 然后++ 从0重新查找

        }

        i++;

        j++;

    }

    return ans;

}

KMP 中 Next[]数组的一个性质：

若一个字符串由循环节不断循环而成  len-Next[len] 为最小循环节的长度

len/（len-Next[len]） 为循环次数

@一些KMP的模板题目（用上面的模板做的）

剪花布条          （用到了模板中的kmp3函数）

Radio Transmition     (Next[]数组的性质)   n-Next[n]

学习中。。有错误请指正  谢谢