软件工程（2019）第三次个人作业

目录

• 软件工程第三次作业
  • 问题描述
  • 分析并设计程序
  • 程序流程图
  • 选择覆盖标准并设计测试样例

软件工程第三次作业

项目地址

问题描述

题目(1)：最大连续子数组和（最大子段和）
背景

问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
-- 引用自《百度百科》

分析并设计程序

  动态规划, 不难得出，针对这个问题，递推公式是DP[i] = max{DP[i-1] + A[i],A[i]}；既然转移方程出来了，意味着写一层循环就可以解决这个问题。

#include <stdio.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
int MaxsumUlt(int * arr, int size)
{
	if (arr == NULL || size == 0)
		return 0;
	int maxSum = 0;
	int sum = 0;
	for (int i = 0; i < size; ++i)
	{
		if (sum < 0)
		{
			sum = arr[i];
		}
		else
		{
			sum += arr[i];
		}
		if (sum > maxSum)
		{
			maxSum = sum;
		}
	}
	return maxSum;
}

int main() {
	int n;
	while (cin >> n) {
		int *a = new int[n];
		for (int i = 0; i < n; i++)
			cin >> a[i];
		printf("%d 
", MaxsumUlt(a, n));
		delete[] a;
	}

}

程序流程图

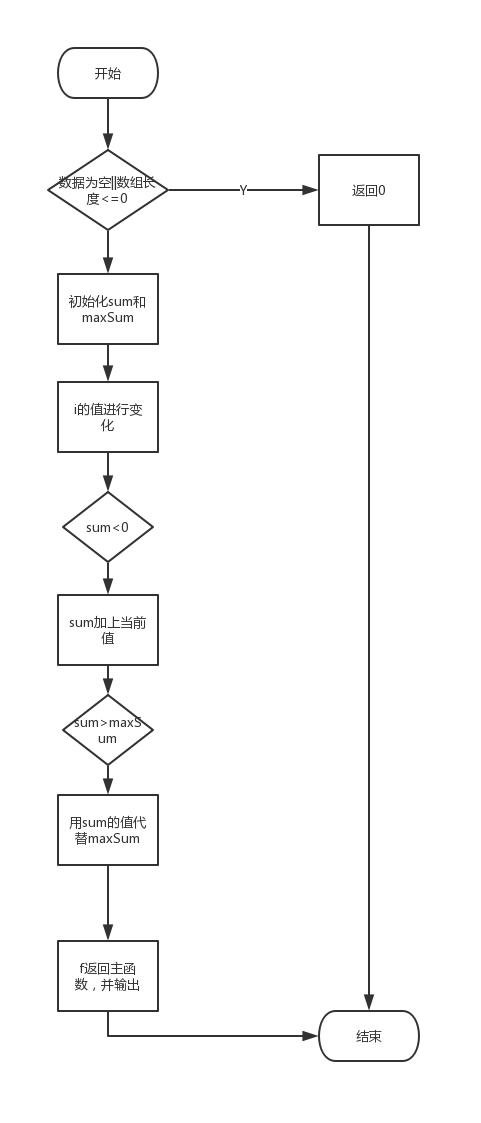
如下

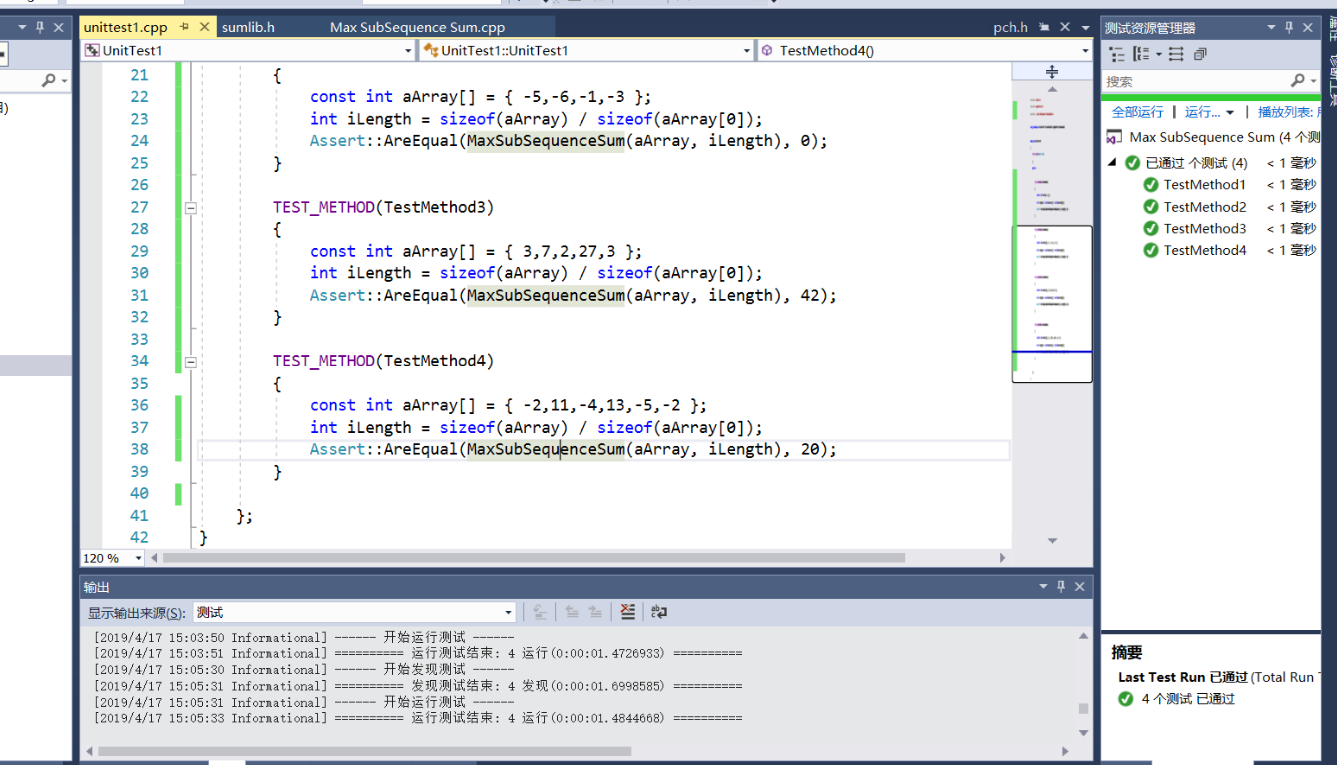
选择覆盖标准并设计测试样例

判定覆盖/条件覆盖

• 数组长度或长度为0
  • 数组为空，长度 ≤ 0判，T1判定为True
  • 数组为空，长度 > 0， T1判定为True
  • 数组不为空，长度 ≤ 0，T1判定为True
  • 数组不为空，长度 > 0，T1判定为False
• sum < 0
  • sum < 0 .T2 True
  • sum > 0 .T2 False,T3 True
• sum > Maxsum
  • sum > Maxsum. T4 True
  • sum < Maxsum. T4 False

设计测试样例如下

| 序号 |数组长度或长度为0 | sum < 0 |sum > Maxsum|样例|
| -------- | -----: | :----: |
|1|T|||无|
|2 | F | F | T | 1,2,3,4,5,6|
| 3 | F | T | F |-1,-3,-5,-1|
|4|F|T|T|-2,11，-4，-13，-5，-2|