题目描述
实现函数double Power(double base, int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。
思路分析
- 要考虑到指数为负数的情况,而且指数为负数的时 base不能为0,因为指数为负数时,是指数的绝对值次幂的倒数,(分母不能为0),考虑到这些情况之后,就可以转化为求exponent的绝对值 次幂的问题,即指数为正数的情况
现在考虑如何求数值的整数次幂(指数为正数的情况):
- 一种方法是直接求,循环exponent次 求得exponent个base的乘积,
第二种巧妙的方法,可以利用斐波那契数列的思想,这里利用递归方法,
- 当指数为偶数时:可以表示成 两个
base的ex/2次幂 的乘积 - 奇数时:可以表示成 两个
base的ex/2次幂 乘积 再乘以base(这里的ex/2是在程序中的运算,5/2 = 2) - 公式如下:
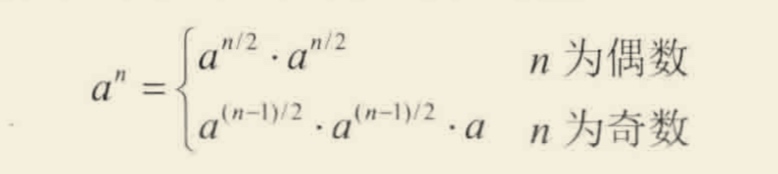
- 当指数为偶数时:可以表示成 两个
测试用例
指数和底数都分别设置为正数、负数和0.
Java代码
public class Offer16 {
public static void main(String[] args) {
test1();
test2();
test3();
}
public static double powCustom(double base, int exponent) {
return Solution2(base, exponent);
}
/**
* 解法一, 要考虑到边界值, exponent为负数时,还要比如0的负数次方
*
* 其中powCustomCore1 方法是利用 直接求的方法
*
* @param base
* @param exponent
* @return
*/
private static double Solution1(double base, int exponent) {
if (base == 0 && exponent < 0) {
throw new IllegalArgumentException("0的指数不能为负数");
}
int absExponent = exponent;
if (exponent < 0) {
absExponent = -exponent;
}
double result = powCustomCore1(base, absExponent);
if (exponent < 0) {
result = 1.0 / result;
}
return result;
}
/**
* 方法一: 直接求,将exponent个 base 相乘
*
* @param base 基数
* @param exponent 指数
* @return
*/
private static double powCustomCore1(double base, int exponent) {
double result = 1.0;
for (int i = 1; i <= exponent; i++) {
result *= base;
}
return result;
}
/**
* 解法二, 要考虑到边界值, exponent为负数时,还要比如0的负数次方
*
* 其中 powCustomCore2 方法是利用 递归的方法
*
* @param base
* @param exponent
* @return
*/
private static double Solution2(double base, int exponent) {
if (base == 0 && exponent < 0) {
throw new IllegalArgumentException("0的指数不能为负数!");
}
int absExponent = exponent;
if (exponent < 0) {
absExponent = -exponent;
}
double result = powCustomCore2(base, absExponent);
if (exponent < 0) {
result = 1.0 / result;
}
return result;
}
/**
* 方法二:
*
* exponent为偶数时,可以将其简化为 两个base的 ex/2 次幂 相乘 exponent为奇数时,可以将其简化为,两个base的 ex/2 次幂
* 相乘之后再乘以base
*
* @param base 基数
* @param exponent 指数
* @return
*/
private static double powCustomCore2(double base, int exponent) {
if (exponent == 0) {
return 0;
}
if (exponent == 1) {
return base;
}
double result = powCustomCore2(base, exponent >> 1);
result *= result;
if ((exponent & 1) == 1) {
result *= base;
}
return result;
}
private static void test1() {
System.out.println("3,3---->" + powCustom(3, 3));
}
private static void test2() {
System.out.println("3,-3----->" + powCustom(3, -3));
}
private static void test3() {
System.out.println("-3,3------>" + powCustom(-3, 3));
}
}