数据结构--堆的实现(下)

1，堆作为优先级队列的应用

对于普通队列而言，具有的性质为FIFO，只要实现在队头删除元素，在队尾插入元素即可。因此，这种队列的优先级可视为按 时间到达 的顺序来衡量优先级的。到达得越早，优先级越高，就优先出队列被调度。

更一般地，元素 不能单纯地按时间到来的先后来分优先级（或者说插入的顺序），在这种情形下，使用堆更容易表达优先级队列。

Sometimes the processing order of the items in a queue needs to be based on characteristics of those items,
 rather than just the order they are created or added to the queue.

2，堆的两个性质：①结构性质--堆从结构上看是一颗完全二叉树。然而，从物理存储上看，堆的实现基本上是使用一个一维数组存储堆中所有的结点。②ordering property---这是由堆的定义决定的，如大顶堆：根结点的值要大于左右孩子的值。

由于堆具有这两个性质，故在对堆进行操作时，如插入操作、删除操作……都需要维护好这两个性质，因此：这也是为什么堆的插入、删除操作经常需要进行向上调整和向下调整，这就是为了维护堆的 ordering property。

3，建堆时间复杂度的分析

在数据结构--堆的实现(上)中，分析了建堆的两种方法，时间复杂度一种为O（nlogn)，一种为O(n)。现在仔细分析如下：

import java.io.File;
import java.io.FileNotFoundException;
import java.util.Scanner;

public class Sort {
    public static void main(String[] args) throws FileNotFoundException{
        Scanner sc = new Scanner(new File("inputfile"));//read heap's element from inputfile
        int n = sc.nextInt();//first line in the file gives number of integers to be read
        ArrayMaxHeap<Integer> sortHeap = new ArrayMaxHeap<Integer>(n);
        //build heap
        for(int i = 0; i < n; i++)
            sortHeap.add(sc.nextInt());//O(nlogn)
        
        //sort phase
        while(!sortHeap.isEmpty())
            System.out.println(sortHeap.removeMax());
    }
}

在上面for循环中的建堆操作中，添加堆中的第一个元素时，完全二叉树高度为1，调用add方法进行堆调整的最坏情况需要 Log1 时间。添加第二个元素时，完全二叉树高度为2，进行堆调整的最坏情况需要 log2 时间……添加第 i 个元素时，最坏需要 logi 时间进行堆调整。故将 n 个元素添加到堆中需要时间：

log1 + log2 + log3 + …… + log(n-1) + logn = log(1*2*3……*n) = log n!

n! = (n/e)ⁿsqrt(2n*pi)

故 O(logn!) = O(nlogn)

同理，也可分析下 while 循环中的堆排序。removeMax()的时间复杂度为logn，n为当前堆中元素的个数。故堆排序的时间复杂度为O(nlogn)

从这里可以看出，此种建堆的方法是调用堆定义的接口来实现的。即调用 堆的接口add()来实现。

另一种建堆的方式则是直接操作堆的底层存储---一维数组 来建堆。此方法建堆的时间复杂度为O(n)

Integer[] arr = new Integer[4];arr[0] = 20;arr[1] = 40;arr[2] = 30;arr[3] = 10;
ArrayMaxHeap<Integer> heap2 = new ArrayMaxHeap<Integer>(arr);

public ArrayMaxHeap(T[] entries){
        heap = (T[]) new Comparable[entries.length + 1];//how to use generic array...
        lastIndex = entries.length;
        for(int index = 0; index < entries.length; index++)
        {
            heap[index + 1] = entries[index];//第0号位置不存放元素
            System.out.println(heap[index + 1]);
        }
        for(int index = lastIndex / 2; index >= 1; index--)
            reheap(index);//从最后一个非叶结点到根结点调用reheap进行堆调整操作
    }

在第12行的for循环中，从最后一个非叶结点(lastIndex/2)开始，直接调用reheap()操作Integer数组。

private void reheap(int rootIndex){
        boolean done = false;//标记堆调整是否完成
        T orphan = heap[rootIndex];
        int largeChildIndex = 2 * rootIndex;//默认左孩子的值较大
        //堆调整基于以largeChildIndex为根的子树进行
        while(!done && (largeChildIndex <= lastIndex)){
            //largeChildIndex 标记rootIndex的左右孩子中较大的孩子
            int leftChildIndex = largeChildIndex;//默认左孩子的值较大
            int rightChildIndex = leftChildIndex + 1;
            //右孩子也存在,比较左右孩子
            if(rightChildIndex <= lastIndex && (heap[largeChildIndex].compareTo(heap[rightChildIndex] )< 0))
                largeChildIndex = rightChildIndex;
            if(orphan.compareTo(heap[largeChildIndex]) < 0){
                heap[rootIndex] = heap[largeChildIndex];
                rootIndex = largeChildIndex;
                largeChildIndex = 2 * rootIndex;//总是默认左孩子的值较大
            }
            else//以rootIndex为根的子树已经构成堆了
                done = true;
        }
        heap[rootIndex] = orphan;
    }

reheap的伪代码如下：

input:array A[0...n-1]
output: max heap in A[0...n-1]

x = n/2 - 1
while(x>=0)
    v=value at x
    siftdown(v)
    x=x-1
endwhile

时间复杂度为O(n)的分析：

假设堆的高度为 h，当reheap某个结点时，需要对 以该结点为根 的子树进行向下的调整。向下调整时根结点有两次比较（与左右孩子的比较）。

因此，假设某结点在第 i 层，0<= i <h，该结点一共需要 2(h-i)次比较。（最后一层叶结点是不需要比较的，因为建堆是从非叶结点开始）

由于是完全二叉树，故第 i 层的结点个数为 2ⁱ

总比较次数为：除去最后一层叶子结点外，其它层的所有的结点的比较次数之和.设总比较次数为S

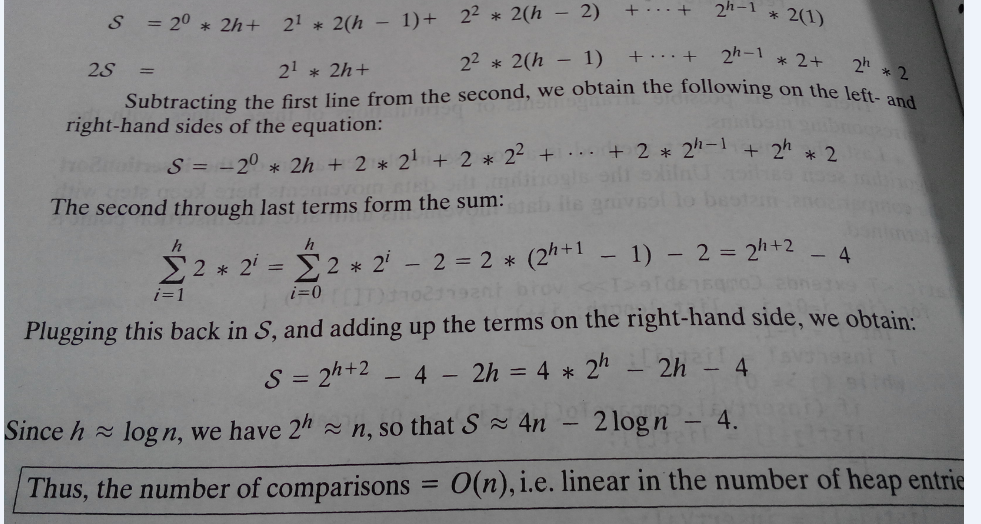
因此，终于明白这种建堆方法的时间复杂度为O(n)了。

参考：数据结构--堆的实现(上)