二分
三分
其实三分是在二分的基础上修改过来的,通常我们二分是进行二分“单调”的东西。而三分就是三分具有凹凸性的东西。我们先举个例子:
假如我们知道了一个函数的定义域[L, R],还知道是一个向下“凹”的函数,且给出了函数表达式f(x),那么怎么求这个函数在定义域内的最小值以及最小值点(最小值点就是黄色的点):

我们取mid = (L+R)/2,p = (mid+R)/2。显然,有mid < p 。当f(mid) < f(p)时,有两种情况:
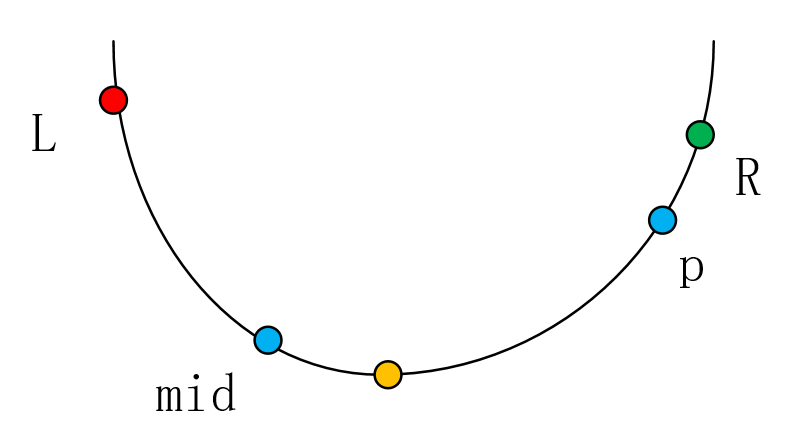
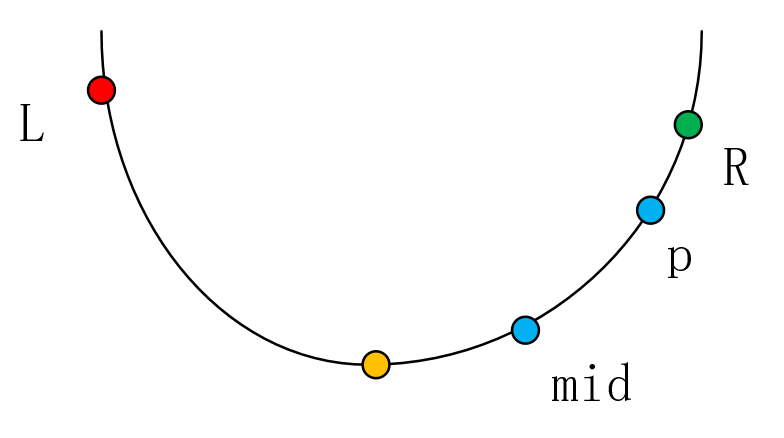
我们发现:无论是哪种情况,我们要求的“最小值点”(黄色的点)始终在p的左侧。所以,我们可以进一步缩小区间,也就是把区间缩小到[L, p]:

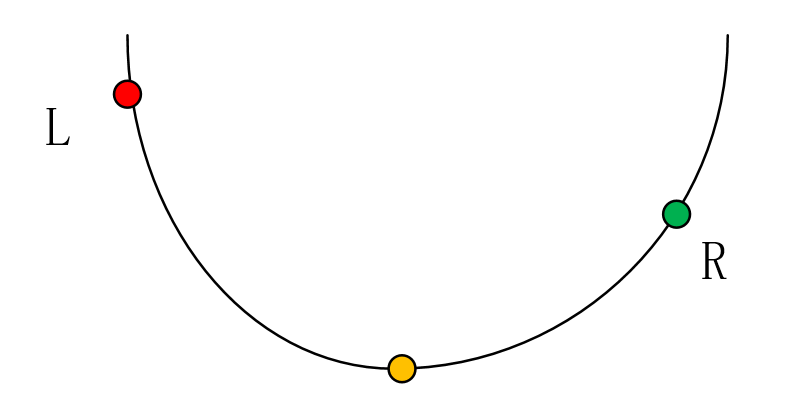
当f(mid) > f(p)时,也有两种情况:

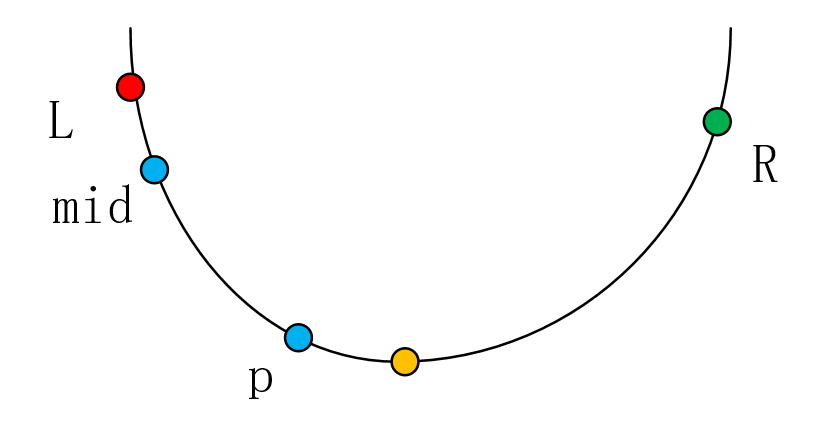
同理可得,无论哪种情况黄色点始终在mid的右边,所以查找范围可以缩成[mid, R]。
所以模板如下(由于用的是double,所以在这里要设置精度):
1 double L, R; 2 double mid, p; 3 double eps; //精度,一般题目会说明 4 5 while(fabs(R-L) > eps){ 6 mid = (L+R)/2; 7 p = (mid+R)/2; 8 if(f(mid) < f(p)){ //f()是根据题目写的计算f(x)的函数 9 R = p; 10 } 11 else L = mid; 12 }
例题练手: