插入排序

一. 直接插入排序（稳定）

算法原理

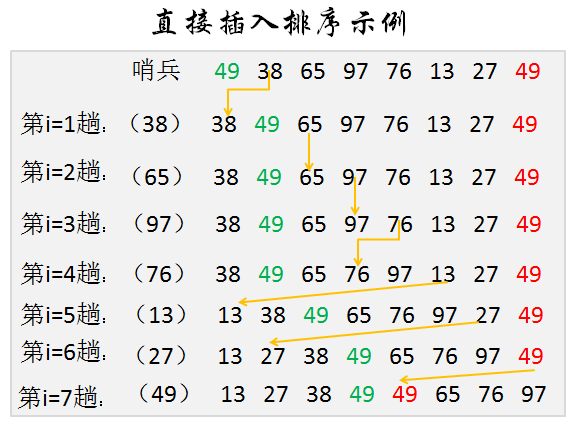
将一个记录插入到已经排好序的有序表中，从而得到一个新的，长度增加1的有序表。

【每遍操作】

现将元素复制到0号位置（哨兵），再将本元素同已排序的序列，从尾开始比较。在已排序的序列中寻找自己的位置，进行插入；或者寻找不到，则一直进行到哨兵为止，即本元素最小，应放置在1号位置。

算法代码

   template <typename Comparable>
   void insertSort( vector<Comparable>& a )
   {
       for ( int i = 1; i < a.size(); ++i )
       {
             Comparable temp = a[i];
          int j = i - 1;
            for ( ; j >= 0 &&a[j] > temp ; --j)
                        a[j+1] = a[j];
           a[j+1] = temp;
      } 
  }

 python版本

def insertSort(data):
    """直接插入排序(有小到大)"""
    n = len(data)
    for i in range(1, n):
        temp = data[i]
        j = i - 1
        while j >= 0 and data[j] > temp:
            data[j+1] = data[j]
            j -= 1

        data[j+1] = temp

    return data

 性能分析：

空间复杂度O(1)

时间复杂度：O(N2)

• 正序时：比较次数n-1次，移动次数0次
• 逆序时：比较次数和移动次数都是O(N2)

 二. 折半插入排序（稳定）

算法原理

 在插入排序基础上进行改进。每次在有序表中查找插入位置时，不按照顺序挨个查找，而是先与有序表中中间的元素进行比较，这样可以查找范围缩至原来的一半。

需要注意的问题

 【具体操作】

        在将一个新元素插入有序表中时，将首元素设为a[low]，末元素设为a[high]，将待插入元素a[i]

与中间元素m=（low+high）/2相比较，如果比它大，则更新low = m+1,否则 high = m-1,直到low<=high不成立，即将此位置之后所有元素后移一位，并将新元素插入到a[high+1].

需要注意的问题

１.必须采用顺序存储方式

２.折半插入排序的比较次数与记录移动次数与初始状态无关，仅依赖于记录的个数。

 

算法代码

void halfInsertSort ( vector<Comparable>& a )
{
    for (int i = 1; i < a.size(); ++i)
   {
         Comparable temp = a[i];
         int low = 0, high = i-1;
         while ( low <= high )
         {
             int mid = ( low + high ) / 2;
             if ( a[mid] <= temp )
                    low = mid + 1;
             else
                    high = mid - 1;
         }//插入位置为low，low到i-1的元素后移
       for ( int j = i - 1; j >= low; --j )
           a[j+1] = a[j];
       a[low] = temp;  
    }  
}

 python版本

def halfInsertSort(data):
    """折半插入"""
    for i in range(1, len(data)):
        temp = data[i]
        low, high = 0, i-1
        while low <= high:
            mid = (low + high) // 2
            if data[mid] <= temp:
                low = mid + 1
            else:
                high = mid - 1
        # 插入位置为low, low~i-1后的元素后移
        for j in range(i-1, low-1, -1):
            data[j+1] = data[j]

        data[low] = temp

    return data

算法性能

• 时间复杂度：O(N2)
• 空间复杂度：O(1)
• 优势：减少比较次数，移动次数不变

三.希尔排序

template< typename Comparable >
void shellSort (vector<Comparable>&a)
{//使用希尔增量，a.size()/2, a.size()/4,...1
   for (int gap = a.size()/2; gap > 0; gap /= 2)
      for (int i = gap; i < a.size(); ++i)
      {
          Comparable temp = a[i]; 
　　　　int j = i-gap;   
          for (; j >= 0 && a[j] > temp; j-=gap)//直接插入法
                a[j+gap] = a[j];//边查找边后移
          a[j+gap] = temp;
       } 
}