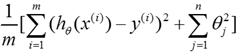deep learning （五）线性回归中L2范数的应用

cost function 加一个正则项的原因是防止产生过拟合现象。正则项有L1，L2 等范数，我看过讲的最好的是这个博客上的：机器学习中的范数规则化之（一）L0、L1与L2范数。看完应该就答题明白了。

这里我们说一下线性回归中L2范数的应用。假设我们的与各维度变量（这里每一个样本只有一维x）关系的模型是：，表示是模型根据各维度变量预测的。    注意这个模型表明我们这里假设与各维度变量的关系不是线性的，如果是线性的那么就是h(X)=ax1+bx2+…,样本每一维都是一次平方，然后叠加，这里只有一维，线性的话就应该是Y=ax。而这里有x的高阶，所以不是。 我们的cost function 采用的是最小均方误差法: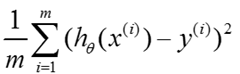.如果我们加上L2的正则项，那么就是：

。（注意是加了正则项再1/m，但是不管是是加不加1/m、1/2m 都不改变求θ的那个公式，自己可以推一下，这里的系数只是影响cost function的值）。不加正则项的求θ的公式是： ，这里X，y分别是按行包含所有样本的矩阵和向量。按理说这个模型不能用前面的那个公式，因为前面的那个公式只是在得到的，这里关系并不是那种线性关系。但是这里我们可以变换一下，θ0就是常数项，θ1就是x1，θ2就是x2…因为你看这里的h（x）的形式跟那个差不多，所以可以替代。也就是说还是用θ那个公式，只是公式里面的X的第一列是1第二列是每一个样本的x本身（这里样本只有一维），第三列是每一个样本的x平方…                

加上L2正则项以后的求参数的公式是.对角矩阵的维度是X的列数。

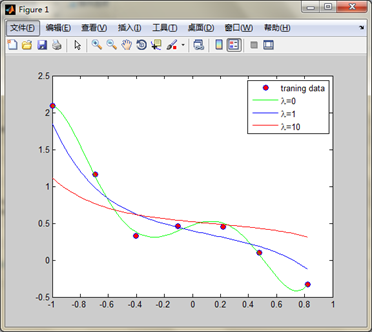
matlab程序：

x = load('ex5Linx.dat');
y = load('ex5Liny.dat');
plot(x,y,'o','MarkerEdgeColor','b','MarkerFaceColor','r')
%如果不加'o','MarkerEdgeColor','b','MarkerFaceColor','r'这些那么自动会把这些点连起来。
x = [ones(length(x),1) x x.^2 x.^3 x.^4 x.^5];%制作矩阵X，前面讲了怎么变换。
[m, n] = size(x);
n = n -1;
rm = diag([0;ones(n,1)]);%lamda后面的对角矩阵
lamda = [0 1 10]';%正则项系数分别取0,1,10
colortype = {'g','b','r'};%不同的曲线不同的颜色
sida = zeros(n+1,3);%初始化θ，每一列代表不同的正则项系数得到的参数向量
xrange = linspace(min(x(:,2)),max(x(:,2)),100)';
%生成一个从x最小值到最大值之间有均匀的100个元素的向量
hold on;
for i = 1:3
    sida(:,i) = inv(x'*x+lamda(i).*rm)*x'*y;%计算参数sida
    norm_sida = norm(sida)
    yrange = [ones(size(xrange)) xrange xrange.^2 xrange.^3,...
        xrange.^4 xrange.^5]*sida(:,i);%xrange是一个100维的向量，
    %xrange.^2是对这个向量每一个元素都进行平方
    plot(xrange,yrange,char(colortype(i)))
    hold on
end
legend('traning data', '\lambda=0', '\lambda=1','\lambda=10')%注意转义字符的使用方法
hold off

结果：