Hark的数据结构与算法练习之归并排序

算法说明：

归并排序的思路就是分而治之，将数组中的数字递归折半进行排序。 递归到最底层就只剩下有两个数字进行比较，再从底层往下进行排序合并。最终得出结果。

同样，语言描述可能对于不知道这个算法的人来说，理解的比较吃力，所以还是举个例子来简单说明一下。

首先，测试数据是int[] arrayData = { 5, 9, 6, 7, 4, 1, 2, 3, 8 }; 一共是9个元素。 

然后拿visio画图，来对于归并排序的分而治之进行一下简单的剖析。

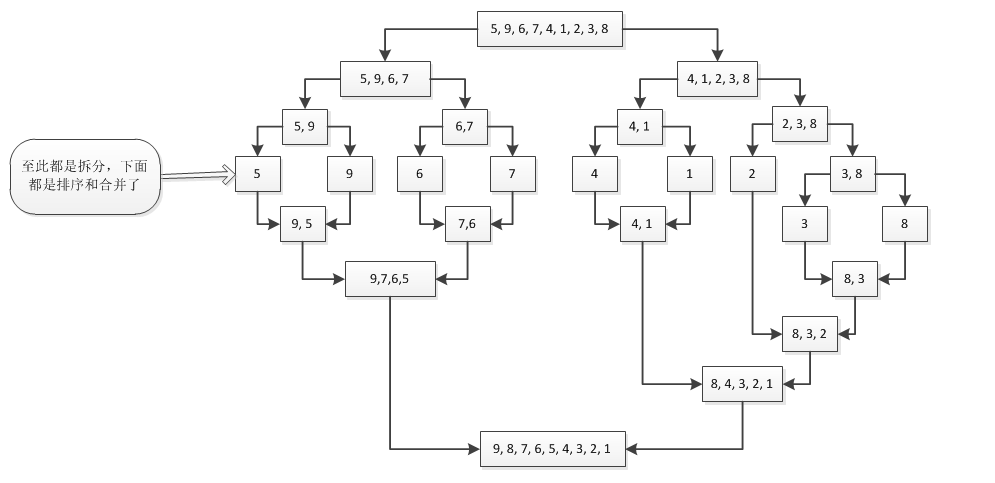
整体排序流程大概就是如上图了。 首先先是递归拆分，递归拆分到最底层后，再进行排序，如果参考下边的代码的话，那么Sort方法就是在往最底层递归，Merge方法就是在进行合并。

另外吐个嘈，上边那个图画的很累啊……

时间复杂度：

O(nlgn)

空间复杂度：

O(n+lgn)

代码：

语言：Java

/*
 * 归并排序
 */
public class MergeSort {
	public static void main(String[] args) {
		int[] arrayData = { 5, 9, 6, 7, 4, 1, 2, 3, 8 };
		int[] arrayResult = MergeSortMethod(arrayData);
		for (int integer : arrayResult) {
			System.out.print(integer);
			System.out.print(" ");
		}
	}

	public static int[] MergeSortMethod(int[] arrayData) {
		int[] arrayResult = new int[arrayData.length];
		Sort(arrayData, 0, arrayData.length - 1, arrayResult);
		return arrayResult;
	}

	public static void Sort(int[] arraySource, int leftIndex, int rightIndex,
			int[] arrayResult) {
		if (leftIndex < rightIndex) {
			int middleIndex = (leftIndex + rightIndex) / 2;
			Sort(arraySource, leftIndex, middleIndex, arrayResult);
			Sort(arraySource, middleIndex + 1, rightIndex, arrayResult);
			Merge(arraySource, leftIndex, middleIndex, rightIndex, arrayResult);
		}
	}

	// 进到merge时，leftIndex至middleIndex的数据已被排好序了。
	// middleIndex+1至rightIndex的数字也已经被排好序了
	// 所以merge就是把排好序的数字合并到arrayResult中
	public static void Merge(int[] arraySource, int leftIndex, int middleIndex,
			int rightIndex, int[] arrayResult) {
		int i = leftIndex;
		int j = middleIndex + 1;
		int k = 0;
		// leftIndex至middleIndex 与 middleIndex+1至rightIndex
		// 进行比较，左右两个数组哪个先循环完毕就跳出while
		while (i <= middleIndex && j <= rightIndex) {
			if (arraySource[i] <= arraySource[j]) {
				arrayResult[k++] = arraySource[j++];
			} else {
				arrayResult[k++] = arraySource[i++];
			}
		}

		while (i <= middleIndex) {
			arrayResult[k++] = arraySource[i++];
		}

		while (j <= rightIndex) {
			arrayResult[k++] = arraySource[j++];
		}

		for (int l = 0; l < k; l++) {
			arraySource[leftIndex + l] = arrayResult[l];
		}
	}
}

结果：

9 8 7 6 5 4 3 2 1 

时间复杂度论证：Merge方法的时间复杂度是n ，然后Sort方法因为是二叉树性质的递归，所以时间复杂度是log₂n，那么归并排序的复杂度就是O(nlog₂n)。  log₂n的时间耗费对于数学基础不好的朋友来说可能理解起来很吃力（例如我），所以大家可以参考http://xwrwc.blog.163.com/blog/static/46320003201141582544245/

空间复杂度论证： Merge因为要使用一个临时数组，所以空间复杂度是n。又另因为是递归迭代的，所以递归也占用空间复杂度log₂n。所以归并排序的空间复杂度是O(n+log₂n)