算法-最大子序列和

最大子序列和的问题，数据结构与算法一书分析中给出了四种算法，最优的算法的时间复杂度为O(N),

// MaxSubsequenceSum.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <iostream>
using namespace std;
int MaxSubsequeSum(const int *A,int N)
{
    int sumTemp=0;
    int sumResult=0;

    for(int index=0;index<N;index++)
    {
        sumTemp+=A[index];
        if(sumResult<sumTemp)
        {
            sumResult = sumTemp;
        }
        else if(sumTemp < 0)
        {
            sumTemp = 0;
        }
    }
    return sumResult;
}


int _tmain(int argc, _TCHAR* argv[])
{
    int  a[10] = {-1,2,1,-1,1,-3,6,-4,1,-3};
    cout<<MaxSubsequeSum(a,10)<<endl;
    return 0;
}

算法的正确性分析没有给出过程，分析过程如下：

此算法将整个数组序列分成了不同的子序列，子序列有如下规则

• 若子序列只有一个元素，那么此元素的值必定为负数
• 若元素个数n>1,那么第一个元素值sub_array[0]一定为大于0的数，并且最后一个元素sub_array[n-1]必定为小于0的数(如果sub_array[n-1]>=0,因为sum(sub_array[0],...,sub_array[n-2])必定大于等于0，那么sum(sub_array[0],...,sub_array[n-1])>=0，得出sub_array[n-1]不是最后一个元素，矛盾)。
• 子序列中的最大和值的求出肯定包含第一个元素。

得出最大值有以下两种情况：

• 子序列中最大值中的最大值，这是上述算法得出的结果。
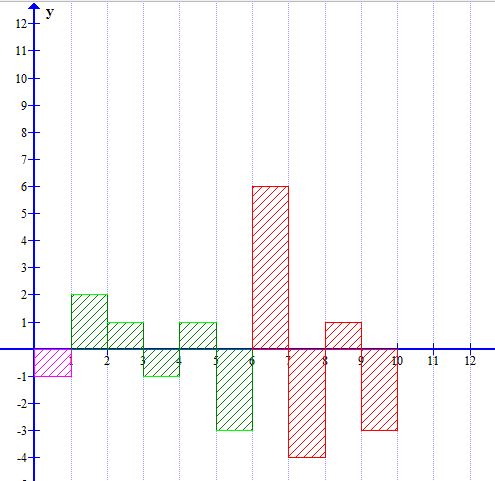
• 还有一种可能，最大值可不可能存在两个或者多个相邻子序列中，这里只需要判断两个子序列即可，也就是最大子序列由第一个子序列的结尾部分和第二个子序列组合而成。看下图：第二个子序列最大和值为6，第一个子序列最后一个值为-3，结果为max_sub_array_1_AND_2 = max_sub_array_1 + sub_array_2[n-1]+sub_array_2[n-2]+......其中sub_array_2[n-1]+sub_array_2[n-2]+......>0，但这是不可能的。因为除sub_array_2[0]可能大于|sub_array_2[n-1]|外，其余必定小于|sub_array_2[n-1]|，sub_array_2[n-1]+sub_array_2[n-2]+......必定<0.因此第二种可能是不存在的。