求两直线交点程序

//以下是一个直线类 ，其中包括了一个方法（Cross），用于求直线的交点 ， 其实求直线交点不难，但有时在斜率不存在时不好处理，

//所以可以用AX + BX + C =0 这个一般式来描述直线。而不用  Y = KX + B

 

using System;
using System.Collections.Generic;
using System.Text;
using System.Windows.Forms;

namespace 相交
{
    /// <summary>
    /// 定义一条直线，这条直线有三个参数，用一般式：AX+BY+C=0。
    /// 所以这三个参数分别为A、B、C
    /// 之所以这样定义是因为直线有时会出现斜率不存在的情况，如果使用Y=KX+B
    /// 就描述不了这条直线。
    /// 但使用一般式时会出现两个点，两点不好求三个参数，所以分为两种情况
    /// 1、直线的斜率存在：则直接令B=1
    /// 2、直线的斜率不存在：则直接令B=0
    /// 这样就相当于两点两个参数。应可以解决直线斜率不存在的情况。
    ///                                                             --hbhbice
    /// </summary>
    public  class HBLine
    {
        PointD pt1, pt2;
        double A, B, C;

        /// <summary>
        /// 使用两点构造一条线。
        /// </summary>
        /// <param name="p1"></param>
        /// <param name="p2"></param>
        public HBLine(PointD p1, PointD p2)
        {
            this.pt1 = p1;
            this.pt2 = p2;
            try
            {
                if (pt1.Y == pt2.Y && pt1.X == pt2.X)
                {
                    //两点相同，确定不了直线。
                    System.Windows.Forms.MessageBox.Show("两相同点，不能确定同一直线，请查实！"
                        , "错误"
                        , System.Windows.Forms.MessageBoxButtons.OK
                        , System.Windows.Forms.MessageBoxIcon.Exclamation
                        , System.Windows.Forms.MessageBoxDefaultButton.Button1);
                }
                else if (pt1.X == pt2.X)
                {
                    this.B = 0;
                    this.A = 1;
                    this.C = -(pt1.X);
                }
                else
                {
                    this.B = 1;
                    this.A = -(this.pt2.Y - this.pt1.Y) / (this.pt2.X - this.pt1.X);
                    this.C = this.pt1.X * (this.pt2.Y - this.pt1.Y) / (this.pt2.X - this.pt1.X) - this.pt1.Y;
                }

            }
            catch (Exception ex)
            {
                System.Windows.Forms.MessageBox.Show(ex.Message);
            }

        }

        /// <summary>
        /// 求两条直线交点
        /// </summary>
        /// <param name="otherLine"></param>
        /// <returns>平行，return null ; 相交，return 交点</returns>
        public PointD Cross(HBLine otherLine)
        {
            try
            {
                double x = 0;
                double y = 0;

                if (this.B == 0 && otherLine.B == 0)  //两直线都无斜率，平行
                {
                    System.Windows.Forms.MessageBox.Show("两直线平行,无交点！");
                    return null;
                }
                else if (this.B == 0)  //其中一条无斜率
                {
                    x = -this.C;
                    y = -(otherLine.A * x + otherLine.C) / otherLine.B;
                }
                else if (otherLine.B == 0) //其中一条无斜率
                {
                    x = -otherLine.C;
                    y = -(this.A * x + this.C) / this.B;
                }
                else  //两条都有斜率，所以 B 都自动为1  
                {
                    if ((this.A / this.B) == (otherLine.A / this.B))
                    {
                        System.Windows.Forms.MessageBox.Show("两直线平行,无交点！");
                        return null;
                    }
                    else
                    {
                        //y = -(otherLine.C / otherLine.A - this.C / this.A) / (otherLine.B / otherLine.A - this.B / this.A);
                        //x = -(this.B * y / this.A + this.C / this.A);
                        x = (this.C - otherLine.C) / (otherLine.A  - this.A );
                        y = -(this.A * x) - this.C; 
                    }
                }
                PointD point = new PointD(x, y);
                return point;
            }
            catch (Exception ex)
            {
                MessageBox.Show("Cross 异常");
                System.Windows.Forms.MessageBox.Show(ex.Message);
                return null;
            }

        }
    }

    public class PointD
    {

        public  double X;
        public double Y;

        public PointD(double x ,double y)
        {
            this.X = x;
            this.Y = y;
        }
    }
}

下在是一个界面，用于测试效果， 以下左图是斜率为0和斜率不存在的两条直线的相交效果。 右图是 一般的直线的相交效果

  

 

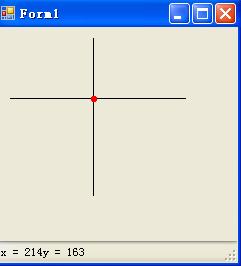
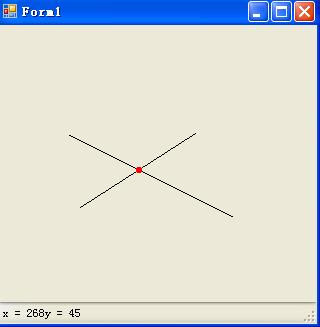
界面部分代码如下：

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Text;
using System.Windows.Forms;

namespace 相交
{
    public partial class Form1 : Form
    {
        PointD []pt = new PointD[4];
        int MouseDownCount = 0;

        public Form1()
        {
            InitializeComponent();
        }

        private void Form1_MouseMove(object sender, MouseEventArgs e)
        {
            toolStripStatusLabel1.Text = "x = " + e.X + "\t" + "y = " + e.Y;
        }

        private void Form1_MouseDown(object sender, MouseEventArgs e)
        {

            switch (MouseDownCount % 4)
            {
                case 0:
                    for (int i = 0; i < pt.Length ; i++)
                    {
                        pt[i] = null;
                    }
                    pt[0] = new PointD(e.X, e.Y);
                    break;
                case 1:
                    pt[1] = new PointD(e.X, e.Y);
                    break;
                case 2:
                    pt[2] = new PointD(e.X, e.Y);
                    break;
                case 3:
                    pt[3] = new PointD(e.X, e.Y);
                    break;
                default:
                    MessageBox.Show("switch case 出错");
                    break;
            }
            MouseDownCount++;
            this.Invalidate();
        }

        private void Form1_Paint(object sender, PaintEventArgs e)
        {
            if (pt.Length >1)
            {
                if (pt[0]!=null && pt[1]!=null )
                {
                    e.Graphics.DrawLine(Pens.Black
                        ,new Point( (int)pt[0].X ,(int)pt[0].Y )
                        ,new Point ( (int)pt[1].X ,(int)pt[1].Y ));
                }
                if (pt[2]!=null && pt[3]!=null )
                {
                    e.Graphics.DrawLine(Pens.Black
                        , new Point((int)pt[2].X, (int)pt[2].Y)
                        , new Point((int)pt[3].X, (int)pt[3].Y));
                    HBLine oneLine = new HBLine(pt[0], pt[1]);
                    PointD pd = oneLine.Cross(new HBLine(pt[2], pt[3]));
                    e.Graphics.FillEllipse(new SolidBrush(Color.Red),
                        new Rectangle((int)pd.X - 3, (int)pd.Y - 3,7, 7));
                }
            }
        }
    }
}