数据准备<3>:数据预处理

数据预处理是指因为算法或者分析需要，对经过数据质量检查后的数据进行转换、衍生、规约等操作的过程。整个数据预处理工作主要包括五个方面内容：简单函数变换、标准化、衍生虚拟变量、离散化、降维。本篇文章将作展开介绍，并提供基于Python的代码实现。

0. 示例数据集说明

/labcenter/python/dataset2.xlsx

import pandas as pd
import numpy as np
# 读取数据
dataset = pd.read_excel("/labcenter/python/dataset2.xlsx")
# 打印数据集
dataset
Out[58]: 
   col1  col2 col3  col4                col5   col6  col7
0   101    96  aaa  3.85 2017-04-05 17:39:08   0-10   800
1   102    13  bbb  2.78 2017-04-04 03:00:14  10-20  1000
2   103   160  aaa  4.40 2017-04-03 14:45:29  10-20   600
3   104   128  ccc  2.49 2017-04-22 11:17:12  20-30  2400
4   105    10  ccc  3.70 2017-04-22 16:42:08  30-40  1300
5   106    16  bbb  2.78 2017-04-19 12:26:58   0-10  1500
6   107   -31  aaa  3.34 2017-04-04 12:50:28  40-50   700
7   108    87  ccc  5.69 2017-04-13 10:15:24  20-30  1200
8   109  -221  bbb  3.35 2017-04-28 13:32:30  30-40  1900
9   110   115  aaa  5.10 2017-04-24 22:28:55  10-20  2000

## 1. 简单函数变换 **简单函数变换**是指对原始数据直接使用某些数学函数进行转换，主要用于**将不具有正态分布的数据变换成具有正态分布**，同时也可以用于**对数据进行压缩**，比如$10^8和10^9$更关注的是相对差距而不是绝对差距，可以通过取对数变换实现。 常用的函数包括：$log(x)、x^k、e^x、frac {1}{x}、sqrt{x}、sinx$等。 简单函数变换会改变的原始数据的分布特征，因此使用前必须深入了解数据特征变化是否会影响到后续的分析。

# 简单函数变换
## 取10为底的对数    
np.log10(dataset['col2'])
Out[72]: 
0    1.982271
1    1.113943
2    2.204120
3    2.107210
4    1.000000
5    1.204120
6         NaN
7    1.939519
8         NaN
9    2.060698
Name: col2, dtype: float64

## 取e为的底的指数
np.exp(dataset['col2'])
Out[73]: 
0    4.923458e+41
1    4.424134e+05
2    3.069850e+69
3    3.887708e+55
4    2.202647e+04
5    8.886111e+06
6    3.442477e-14
7    6.076030e+37
8    1.049348e-96
9    8.787502e+49
Name: col2, dtype: float64

## 取倒数
1 / dataset['col2']     
Out[74]: 
0    0.010417
1    0.076923
2    0.006250
3    0.007812
4    0.100000
5    0.062500
6   -0.032258
7    0.011494
8   -0.004525
9    0.008696
Name: col2, dtype: float64

## 开方
np.sqrt(dataset['col2'])
Out[75]: 
0     9.797959
1     3.605551
2    12.649111
3    11.313708
4     3.162278
5     4.000000
6          NaN
7     9.327379
8          NaN
9    10.723805
Name: col2, dtype: float64

## 取正弦
np.sin(dataset['col2'])
Out[76]: 
0    0.983588
1    0.420167
2    0.219425
3    0.721038
4   -0.544021
5   -0.287903
6    0.404038
7   -0.821818
8   -0.885939
9    0.945435
Name: col2, dtype: float64

## 2. 标准化 标准化，是为了处理**不同规模和量纲**的数据，使其缩放到相同的数据区间和范围，以减少规模、量纲、分布差异等对分析建模的影响。**常用的标准化方法有以下三种**： ###2.1 离差标准化 离差标准化，又称**最大值最小值标准化（Max-Min）**，即基于原始数据的最大值、最小值对数据进行线性变换，**变换后，数据完全落入[0,1]区间内**。 **公式：** $$x'= frac {(x-min)}{(max-min)}$$ 其中，原始数据x，其最大值、最小值分别为max、min，转换后数据为x'。 **优点：**能够将数据归一化，同时能较好的保持原始数据的分布结构； **缺点：**容易受极端值的影响，极端值会使大部分数据接近于0并且差距很小，同时在出现最值范围以外的数据时变换结果会产生错误； **适用场景**：适合数据比较集中的情况。 ###2.2 标准差标准化 标准差标准化，即**Z-Score标准化**，即基于原始数据的均值和标准差对数据进行标准化，**标准化后，数据呈正态分布**。 **公式：** $$x'= frac {(x-μ)}{σ}$$ 其中，原始数据x，其均值、标准差分别为μ、σ，转换后数据为x'。 **缺点：**是一种中心化方法，会改变原始数据的分布结构。 **适用场景**：适合数据的最值未知，且可能出现离群点的情况。 ###2.3 绝对值最大标准化 绝对值最大标准化，即**MaxAbs标准化**，即基于原始数据绝对值的最大值对数据进行标准化，**变换后，数据完全落入[-1,1]区间内**。 **公式：** $$x'= frac {x}{maxAbs}$$ 其中，原始数据x，其绝对值的最大值为maxAbs，转换后数据为x'。 **优点：**不会破坏原始数据的分布结构； **适用场景：**可用于稀疏矩阵、稀疏数据。

# 标准化处理
## 方法1：使用numpy
### 离差标准化
(dataset['col2'] - dataset['col2'].min()) / (dataset['col2'].max() - dataset['col2'].min())
Out[77]: 
0    0.832021
1    0.614173
2    1.000000
3    0.916010
4    0.606299
5    0.622047
6    0.498688
7    0.808399
8    0.000000
9    0.881890
Name: col2, dtype: float64

### 标准差标准化
(dataset['col2'] - dataset['col2'].mean()) / dataset['col2'].std()
Out[78]: 
0    0.534846
1   -0.221410
2    1.117982
3    0.826414
4   -0.248744
5   -0.194075
6   -0.622316
7    0.452842
8   -2.353503
9    0.707964
Name: col2, dtype: float64

### 绝对值最大标准化
dataset['col2'] / np.abs(dataset['col2']).max()
Out[79]: 
0    0.434389
1    0.058824
2    0.723982
3    0.579186
4    0.045249
5    0.072398
6   -0.140271
7    0.393665
8   -1.000000
9    0.520362
Name: col2, dtype: float64

## 方法2：使用sklearn
from sklearn import preprocessing
### 离差标准化
minmax_scaler = preprocessing.MinMaxScaler()
minmax_scaler.fit_transform(dataset['col2'])
Out[81]: 
array([ 0.832021  ,  0.61417323,  1.        ,  0.9160105 ,  0.60629921,
        0.62204724,  0.49868766,  0.80839895,  0.        ,  0.88188976])

### 标准差标准化
zsocre_scaler = preprocessing.StandardScaler()
zsocre_scaler.fit_transform(dataset['col2'])
Out[82]: 
array([ 0.56377684, -0.23338633,  1.17845688,  0.87111686, -0.26219945,
       -0.2045732 , -0.65597885,  0.47733746, -2.4808102 ,  0.74625998])

### 绝对值最大标准化
maxabs_scaler = preprocessing.MaxAbsScaler()
maxabs_scaler.fit_transform(dataset['col2'])
Out[83]: 
array([ 0.43438914,  0.05882353,  0.7239819 ,  0.57918552,  0.04524887,
        0.07239819, -0.14027149,  0.39366516, -1.        ,  0.52036199])

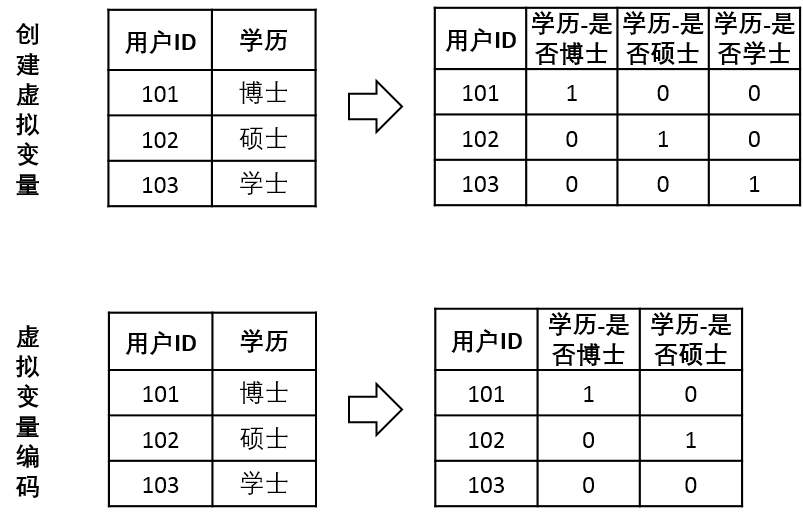
## 3. 衍生虚拟变量 在数据建模过程中，很多算法都不能处理非数值型数据，必须首先将这些数据转化为数值型。但是，即使转化为数值型数据，也不能直接应用到算法计算中，为什么？这需要从离散型数据的分类说起。 **离散型数据也就是分类数据，主要分为两类，一类是无序分类，一类是有序分类。** **无序分类**，是指各个类别之间没有明显的高、低、大、小等包含等级、顺序、优劣、好坏等逻辑的划分，只是用来区分两个或多个具有相同或相当价值的属性。例如性别的男和女，颜色的红、黄、蓝等等。 **有序分类**，是指各个类别之间有一定的顺序关系。例如用户价值的高、中、低，学历的博士、硕士、学士等。 对于无序分类来说，无论用什么数值来表示都无法表达出价值相等但有区分的属性，比如性别的男和女，如果分别用1和2表示，那么1和2本身就已经带有距离为1的差异，但实际上二者之间是没有这种差异的，同样，不论用任何数据都无法到达这种区分的目的。 而对于有序分类来说，无论用什么有序的数字序列都无法准确表达出有序类别之间的差异性，比如学历的博士、硕士、学士，如果用3-2-1来表示这种顺序关系，那这种差异为什么不能用30-20-10来表示呢？ 所以，非数值型的离散型数据要想参与到算法计算中，不能简单的认为转化成用数值就表示就可以，而是必须使用其他的方法，这种方法就是**衍生虚拟变量**，也叫做**创建虚拟变量（dummy variable）、创建哑变量、创建名义变量、one-hot编码（one-hot encoding）、N取一编码（one-out-of encoding）**。它是指，将一个离散型变量衍生出多个真值变量（用0和1，或者True和False表示的变量），比如性别这一变量取值有男、女两个，那么将衍生出性别是否男、性别是否女两个变量；然后使用这些衍生出来的真值变量替换原始变量参与后续的计算。 

# 衍生虚拟变量
## 方法1：自定义函数
def dummyCreate(ser):
    valueSet = ser.unique()
    resDf = pd.DataFrame()
    colName = ser.name
    for value in valueSet:
        colNameNew = colName + '_' + value
        colDataTmp = ser.values
        colData = (colDataTmp == value)
        resDf[colNameNew] = colData
    return resDf

dummyCreate(dataset['col3'])
Out[85]: 
  col3_aaa col3_bbb col3_ccc
0     True    False    False
1    False     True    False
2     True    False    False
3    False    False     True
4    False    False     True
5    False     True    False
6     True    False    False
7    False    False     True
8    False     True    False
9     True    False    False

## 方法2：使用sklearn
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import LabelEncoder
### 标准标签化
labelEnc = LabelEncoder()   
### one-hot编码
ohEnc = OneHotEncoder()   
### 将类别值用0.1.2……编码
dataset['new_col'] = labelEnc.fit_transform(dataset['col3'])   
### one-hot编码
ohEncRes = ohEnc.fit_transform(dataset['new_col'].reshape(-1,1)).toarray()  
### 合并结果
newDf = pd.concat((dataset, pd.DataFrame(ohEncRes)), axis=1)    
### 重命名列名
dataset = newDf.rename(columns={0:'col3_aaa',1:'col3_bbb',2:'col3_ccc'})    
### 打印数据集
dataset
Out[87]: 
   col1  col2 col3  col4                col5   col6  col7  new_col  col3_aaa  col3_bbb  col3_ccc
0   101    96  aaa  3.85 2017-04-05 17:39:08   0-10   800        0       1.0       0.0       0.0
1   102    13  bbb  2.78 2017-04-04 03:00:14  10-20  1000        1       0.0       1.0       0.0
2   103   160  aaa  4.40 2017-04-03 14:45:29  10-20   600        0       1.0       0.0       0.0
3   104   128  ccc  2.49 2017-04-22 11:17:12  20-30  2400        2       0.0       0.0       1.0
4   105    10  ccc  3.70 2017-04-22 16:42:08  30-40  1300        2       0.0       0.0       1.0
5   106    16  bbb  2.78 2017-04-19 12:26:58   0-10  1500        1       0.0       1.0       0.0
6   107   -31  aaa  3.34 2017-04-04 12:50:28  40-50   700        0       1.0       0.0       0.0
7   108    87  ccc  5.69 2017-04-13 10:15:24  20-30  1200        2       0.0       0.0       1.0
8   109  -221  bbb  3.35 2017-04-28 13:32:30  30-40  1900        1       0.0       1.0       0.0
9   110   115  aaa  5.10 2017-04-24 22:28:55  10-20  2000        0       1.0       0.0       0.0

注意：创建虚拟变量和虚拟变量编码（dummy encoding）是不同的概念，前者如上所述，如果一个离散变量有N个取值，就会衍生出N个真值变量，而后者——虚拟变量编码，则是衍生出N-1个变量，它认为这个N-1个变量都为0时即表示原始数据取第N个值。

## 4. 离散化 **离散化就是将一份数据从细粒度转化为粗粒度，实质就是数据的集中化。**主要包括**两方面**：将连续型数据转化成离散型数据、将离散型数据进行类别合并，具体又分为以下几点： ###4.1 针对时间数据的离散化 针对时间数据的离散化主要是指对时间数据进行粒度上的上卷（反之是下钻）： 时间戳——>小时——>上午下午 日期型——>星期——>周数——>季度——>年份

# 离散化
## 针对时间数据的离散化
colList = list(dataset.columns)
colList.extend(['weekday_col5','week_col5','year_col5','month_col5','day_col5','hour_col5'])
dataset = dataset.reindex(columns = colList)
for index,value in enumerate(dataset['col5']):
    newValue = pd.to_datetime(value)
    dataset['weekday_col5'][index] = newValue.weekday()
    dataset['week_col5'][index] = newValue.week
    dataset['year_col5'][index] = newValue.year
    dataset['month_col5'][index] = newValue.month
    dataset['day_col5'][index] = newValue.day
    dataset['hour_col5'][index] = newValue.hour
### 打印数据集
dataset[['col5','weekday_col5','week_col5','year_col5','month_col5','day_col5','hour_col5']]
Out[101]: 
                 col5  weekday_col5  week_col5  year_col5  month_col5  day_col5  hour_col5
0 2017-04-05 17:39:08           2.0       14.0     2017.0         4.0       5.0       17.0
1 2017-04-19 12:26:58           2.0       16.0     2017.0         4.0      19.0       12.0
2 2017-04-04 03:00:14           1.0       14.0     2017.0         4.0       4.0        3.0
3 2017-04-03 14:45:29           0.0       14.0     2017.0         4.0       3.0       14.0
4 2017-04-24 22:28:55           0.0       17.0     2017.0         4.0      24.0       22.0
5 2017-04-22 11:17:12           5.0       16.0     2017.0         4.0      22.0       11.0
6 2017-04-13 10:15:24           3.0       15.0     2017.0         4.0      13.0       10.0
7 2017-04-22 16:42:08           5.0       16.0     2017.0         4.0      22.0       16.0
8 2017-04-28 13:32:30           4.0       17.0     2017.0         4.0      28.0       13.0
9 2017-04-04 12:50:28           1.0       14.0     2017.0         4.0       4.0       12.0

4.2 针对类别数据的离散化

针对类别数据的离散化主要是指将多个类别进行合并而产生新的类别划分。
比如将年龄区间（0-10，10-20，20-30，30-40，40-50）合并为年龄区间（0-20，20-30，30-50）。

## 针对类别数据的离散化
mapDf = pd.DataFrame([['0-10','0-20'],['10-20','0-20'],['20-30','20-30'],['30-40','30-50'],['40-50','30-50']],columns=['col6','new_col2'])
dataset = dataset.merge(mapDf, left_on = 'col6', right_on = 'col6', how = 'inner')
### 打印
dataset[['col6','new_col2']]
Out[102]: 
    col6 new_col2
0   0-10     0-20
1   0-10     0-20
2  10-20     0-20
3  10-20     0-20
4  10-20     0-20
5  20-30    20-30
6  20-30    20-30
7  30-40    30-50
8  30-40    30-50
9  40-50    30-50

4.3 针对连续数据的离散化

离散化中主要的工作是针对连续数据的离散化，包括两方面：将连续数据分成多个区间、将连续数据划分成特定的类。前者通常被称为分箱。具体有以下几种实现方法：

（1）自定义分箱

自定义分箱，是指根据业务经验或者常识等自行设定划分的区间，然后将原始数据归类到各个区间中。

（2）等宽分箱

等宽分箱，是指划分的各个区间的宽度（或称为距离）相等，也称为等深分箱。

（3）等频分箱

等频分箱，是指划分的各个区间包含的数据点的个数相等，也称为分位数分箱。

（4）聚类法

聚类法，是指使用聚类算法自动将原始数据分成多个类别。

（5）二值化

二值化，是指设置一个阈值，将每个数据点与这个阈值进行比较，大于（或等于）阈值取某一固定值A，小于（或等于）阈值则取另一固定值B，从而将原始数据转换为两个取值的离散数据。

## 针对连续数据的离散化
### (1)自定义分箱
#### 定义边界点
points = [0,800,1500,2000,2500]
#### 未设置标签
pd.cut(dataset['col7'], points)
Out[91]: 
0        (0, 800]
1     (800, 1500]
2     (800, 1500]
3        (0, 800]
4    (1500, 2000]
5    (2000, 2500]
6     (800, 1500]
7     (800, 1500]
8    (1500, 2000]
9        (0, 800]
Name: col7, dtype: category
Categories (4, object): [(0, 800] < (800, 1500] < (1500, 2000] < (2000, 2500]]
#### 设置标签
pd.cut(dataset['col7'], points, labels = ['a','b','c','d'])
Out[92]: 
0    a
1    b
2    b
3    a
4    c
5    d
6    b
7    b
8    c
9    a
Name: col7, dtype: category
Categories (4, object): [a < b < c < d]

### (2)等宽分箱
#### 箱数
bins = 4   
#### 未设置标签
pd.cut(dataset['col7'], bins)
Out[94]: 
0    (598.2, 1050]
1     (1050, 1500]
2    (598.2, 1050]
3    (598.2, 1050]
4     (1950, 2400]
5     (1950, 2400]
6     (1050, 1500]
7     (1050, 1500]
8     (1500, 1950]
9    (598.2, 1050]
Name: col7, dtype: category
Categories (4, object): [(598.2, 1050] < (1050, 1500] < (1500, 1950] < (1950, 2400]]
#### 设置标签
pd.cut(dataset['col7'], bins, labels = ['a','b','c','d'])
Out[95]: 
0    a
1    b
2    a
3    a
4    d
5    d
6    b
7    b
8    c
9    a
Name: col7, dtype: category
Categories (4, object): [a < b < c < d]

### (3)等频分箱
#### 箱数
bins = 4   
#### 未设置标签
pd.qcut(dataset['col7'], bins)
Out[97]: 
0      [600, 850]
1    (1250, 1800]
2     (850, 1250]
3      [600, 850]
4    (1800, 2400]
5    (1800, 2400]
6     (850, 1250]
7    (1250, 1800]
8    (1800, 2400]
9      [600, 850]
Name: col7, dtype: category
Categories (4, object): [[600, 850] < (850, 1250] < (1250, 1800] < (1800, 2400]]
#### 设置标签
pd.qcut(dataset['col7'], bins, labels = ['a','b','c','d'])
Out[98]: 
0    a
1    c
2    b
3    a
4    d
5    d
6    b
7    c
8    d
9    a
Name: col7, dtype: category
Categories (4, object): [a < b < c < d]

### (4)聚类法
from sklearn.cluster import KMeans
data = dataset['col7']
new_data = data.reshape((data.shape[0], 1))
#### 使用K-Means聚类
kmeans = KMeans(n_clusters=4, random_state=0)  
keames_result = kmeans.fit_predict(new_data)
keames_result
Out[99]: array([1, 2, 1, 1, 3, 0, 2, 2, 3, 1], dtype=int32)

### (5)二值法
from sklearn import preprocessing
#### 使用均值作为分割阈值
binarizer_scaler = preprocessing.Binarizer(threshold = dataset['col7'].mean())  
temp = binarizer_scaler.fit_transform(dataset['col7'])
temp.resize(dataset['col7'].shape)
temp
Out[100]: array([0, 1, 0, 0, 1, 1, 0, 0, 1, 0])

## 5. 降维 **降维**是指降低数据集的维度数量，从而降低模型的计算工作量，减少模型的运行时间，减弱噪声变量（无关变量）对模型结果可能产生的影响。

5.1 基于特征选择的降维

基于特征选择的降维，通俗的说，就是特征筛选，或者叫变量筛选。从多个变量中筛选出更有用的较少个变量，从而降低数据集的维度。特征筛选的主要方法包括：基于经验的方法（比如专家法）、基于统计的方法（比如区分度、信息增益）和基于机器学习的方法（比如决策树算法）。
基于特征选择的降维的好处是，既保留了原有维度的特征，同时又完成了降维的目的。
由于特征筛选是数据准备工作的一个重要环节，因此会单独拿出来进行总结论述，此处不做详细讨论。

5.2 基于维度转换的降维

基于维度转换的降维，是指按照一定的数学变换方法，把给定的一组（相关的）变量，通过数学模型从高维空间映射到低维度空间中，然后利用映射后产生的新变量来表示原有变量的总体特征，转换后产生的新特征是多个原始特征的综合。
具体的方法分为线性降维和非线性降维，常用的算法有主成分分析、因子分析、线性判别分析等。
关于具体的算法原理，后续将在统计学或机器学习系列中进行总结论述，此处不做讨论。
基于维度转换的降维将使用转换后产生的新变量参与后续的建模分析，因此直接影响到模型的可解释性和可理解性，在不要求对模型进行解释说明时可以使用，否则，建议使用基于特征选择的降维。

## 6. 参考与感谢 [1] [数据挖掘概念与技术](https://book.douban.com/subject/2038599/) [2] [数据挖掘导论](https://book.douban.com/subject/5377669/) [3] [Python机器学习基础教程](https://book.douban.com/subject/30147778/) [4] [Python数据分析与数据化运营](https://book.douban.com/subject/27608466/) [5] [Python数据分析与数据挖掘实战](https://book.douban.com/subject/26677686/)