luogu P4515 [COCI2009-2010#6] XOR

luogu P4515 [COCI2009-2010#6] XOR

描述

坐标系下有若干个等腰直角三角形，且每个等腰直角三角形的直角顶点都在左下方，两腰与坐标轴平行。被奇数个三角形覆盖的面

积部分为灰色，被偶数个三角形覆盖的面积部分为白色，如下图所示。

  

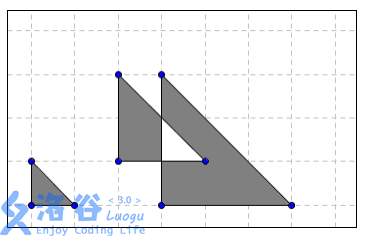
已知 NN个等腰直角三角形的顶点坐标及腰长，求灰色部分面积。

输入输出格式

输入格式：

输入第一行包含一个整数 NN，表示等腰直角三角形数量。

接下来 NN行，每行三个整数 X, Y, RX,Y,R，分别表示等腰直角三角形的顶点坐标 (X, Y)(X,Y)与腰长 RR。

输入输出样例

输入样例#1： 复制

3
1 1 2
7 1 6
5 3 4

输出样例#1： 

24.0

这是自己做出的第一道容斥题（除了一些SB容斥），虽然这道题也不算太难，而且我做了一个晚上。总之就是自己在容斥上还是太菜了。

还是来说题吧。首先要会求多个三角形的交。显然这道题中两个等腰直角的交还是一个等腰直角三角形。我的做法是分类讨论，不如洛谷上题解那么简洁，于是就不说了。

重点是算出容斥系数。我们设个三角形的交的容斥系数为。显然。对于，的情况，我们先设初值，显然如果为奇数，那么初值为1，否则为0。然后我们要容斥去重。。计算个三角形的交的时候，个三角形的交会被计算次。

然后通过观察证明可以知道。

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<ctime>
#include<iomanip>
#define ll long long
#define N 11

using namespace std;
inline int Get() {int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}while('0'<=ch&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}return x*f;}

int n;
ll ans;
ll f[N];
ll c[N][N];
struct tri {ll x,y,r;}s[N],tem,g;
void work(tri a,tri b) {
	if(a.y>b.y) swap(a,b);
	if(a.x<=b.x) {
		int r=min(b.r,a.r-(b.x+b.y-a.x-a.y));
		if(r<0) return g.r=-1,void();
		g=b;
		g.r=r;
	} else {
		int r=min(a.y+a.r-b.y,b.x+b.r-a.x);
		if(r<0) return g.r=-1,void();
		g.x=a.x,g.y=b.y;
		g.r=r;
	}
}
void dfs(int v,ll x,ll y,ll r,int tot) {
	if(r<=0&&tot) return ;
	if(v>n) {
		if(!tot) return ;
		ans+=r*r*f[tot];
		return ;
	}
	dfs(v+1,x,y,r,tot);
	if(!tot) {
		dfs(v+1,s[v].x,s[v].y,s[v].r,tot+1);
	} else {
		tem.x=x,tem.y=y,tem.r=r;
		work(s[v],tem);
		dfs(v+1,g.x,g.y,g.r,tot+1);
	}
}
int main() {
	n=Get();
	c[0][0]=1;
	for(int i=1;i<=n;i++) {
		for(int j=0;j<=i;j++) {
			c[i][j]=(!j||i==j)?1:c[i-1][j-1]+c[i-1][j];
		}
	}
	for(int i=1;i<=n;i++) {
		f[i]=(i&1)?1:0;
		for(int j=1;j<i;j++) {
			f[i]-=f[j]*c[i][j];
		}
	}
	//f[i]=(-1)^(i+1)*2^(i-1)
	for(int i=1;i<=n;i++) {
		s[i].x=Get(),s[i].y=Get(),s[i].r=Get();
	}
	dfs(1,0,0,0,0);
	cout<<fixed<<setprecision(1)<<1.0*ans/2;
	return 0;
}