luogu1273 有限电视网

题目大意

　　有一棵有根树，每个结点有一个收益，每条边有一个花费。如果要选择一个叶子结点，则根节点到该叶子结点的路径上的所有结点都必须被选择。求当总收益大于等于总花费的情况下，最多能选择多少个叶子结点。

思路

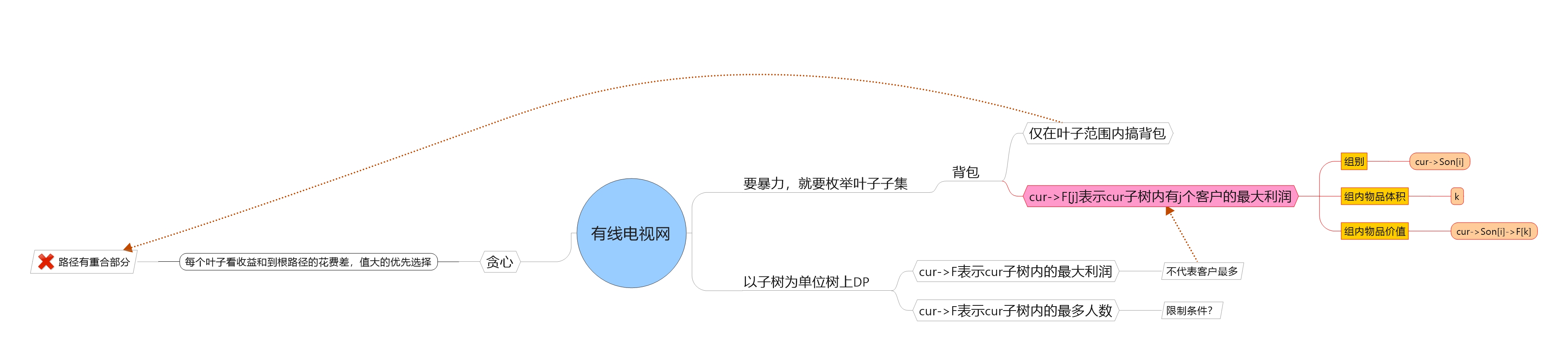
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cassert>
using namespace std;

const int MAX_NODE = 3010, MAX_EDGE = MAX_NODE, MINF = 0xcfcfcfcf;
int TotNode, TotLeaf;

struct Node;
struct Edge;

struct Node
{
    Edge *Head;
    int DP[MAX_NODE];
    int Val;
    int LeafCnt;
}_nodes[MAX_NODE];

struct Edge
{
    Node *To;
    Edge *Next;
    int Cost;
}_edges[MAX_EDGE];
int _eCount;

void AddEdge(Node *from, Node *to, int w)
{
    Edge *e = _edges + ++_eCount;
    e->To = to;
    e->Cost = w;
    e->Next = from->Head;
    from->Head = e;
}

void Dfs(Node *cur)
{
    memset(cur->DP, MINF, sizeof(cur->DP));
    cur->DP[0] = 0;
    if (cur - _nodes > TotNode - TotLeaf)
    {
        assert(!cur->Head);
        cur->DP[1] = cur->Val;
        cur->LeafCnt = 1;
        return;
    }
    for (Edge *e = cur->Head; e; e = e->Next)
    {
        Dfs(e->To);
        cur->LeafCnt += e->To->LeafCnt;
    }
    for (Edge *e = cur->Head; e; e = e->Next)
        for (int j = cur->LeafCnt; j >= 1; j--)
            for (int k = 1; k <= min(j, e->To->LeafCnt); k++)
                cur->DP[j] = max(cur->DP[j], cur->DP[j - k] + e->To->DP[k] - e->Cost);
}

int main()
{
    scanf("%d%d", &TotNode, &TotLeaf);
    for (int i = 1; i <= TotNode - TotLeaf; i++)
    {
        int totOut, to, w;
        scanf("%d", &totOut);
        for (int j = 1; j <= totOut; j++)
        {
            scanf("%d%d", &to, &w);
            AddEdge(_nodes + i, _nodes + to, w);
        }
    }
    for (int i = TotNode - TotLeaf + 1; i <= TotNode; i++)
        scanf("%d", &_nodes[i].Val);
    Dfs(_nodes + 1);
    for (int j = TotLeaf; j >= 0; j--)
    {
        if (_nodes[1].DP[j] >= 0)
        {
            printf("%d
", j);
            return 0;
        }
    }
    return 0;
}