如果$ax{equiv}1(mod\,p)$,且a与p互质(gcd(a,p)=1),则称a关于模p的乘法逆元为x。(不互质则乘法逆元不存在)
有一个问题,在求解过程中有除法,答案很大,要求最终答案对某数p取模。显然,由于除法的出现,每一次运算之后取模是行不通的。(比如:求1*7/2,答案对5取模。如果每一次运算取模也就是7%5/2%5,会得到1,正确结果却是3)如果不想高精度把最终结果算出来再取模的话,有一个方法,就是把除以x转换为乘上x关于模p的乘法逆元。(事实上,乘法逆元应该视为线性同余方程的解也就是一些数而不是一个数,但是一般只需要使用任意一个(比如最小正整数解)就能完成任务)
设c是b关于模m的逆元,即$b*c{equiv}1(mod\,m)$,那么有$a/b{equiv}(a/b)*1{equiv}(a/b)*b*c{equiv}a*c(mod\,m)$
求法:
1.扩展欧几里得
$ax{equiv}1(mod\,p)$,那么可以设$ax-1=p(-y)$,那么$ax+py=1=gcd(a,p)$,求解即可
2.欧拉定理(费马小定理)
质数筛法:
列一张表可以发现,每一个非质数x都是被(x/x的最小质因子)这个数筛掉的。
注意:break那里不能是(!i%prime[j])!!!!!如果这样写一定要写成(!(i%prime[j]))!!感叹号优先级高!!
nprime[1]=1; for(i=2;i<=n;i++) { if(!nprime[i]) prime[++len]=i; printf("%d: ",i); for(j=1;j<=len&&i*prime[j]<=n;j++) { nprime[i*prime[j]]=1; printf("%d ",i*prime[j]); if(i%prime[j]==0) break; } puts(""); }
2: 4 3: 6 9 4: 8 5: 10 15 25 6: 12 7: 14 21 35 49 8: 16 9: 18 27 10: 20 11: 22 33 12: 24 13: 26 39 14: 28 15: 30 45 16: 32 17: 34 18: 36 19: 38 20: 40 21: 42 22: 44 23: 46 24: 48 25: 50
调试跟踪一下就可以明白这个break的原理。
例如当i=12时,第一次筛掉24。显然,24的最小质因子是2,24/2=12。之后发现12是2的倍数,说明12乘一个2以上的质数,得到的合数的最小质因子都是2,就不应当由12来筛掉。
欧拉函数:$φ(n)$表示小于等于n且与n互质的整数个数。定义$φ(1)=1$。
显然,设$n=p1^a1*p2^a2*...*pk^ak$(就是把n分解质因数),那么小于n且不与n互质的整数,一定是集合${p1,p2,..,pk}$中一些数的积。
也就是说,$φ(n)$就是
欧拉函数定义&基础求法&筛法:http://www.cnblogs.com/linyujun/p/5194170.html
欧拉函数exthttps://zhuanlan.zhihu.com/p/24902174
筛法补充说明:对于每一个质数p,欧拉函数值显然等于p-1。对于每一个合数a,用筛掉它的数b的函数值来计算它的函数值。
几个性质的补充说明:
这个证明没有仔细看是不是对的
(以下内容仅留作记录)
欧拉函数,用φ(n)表示
欧拉函数是求小于等于n的数中与n互质的数的数目
辣么,怎么求哩?~(~o ̄▽ ̄)~o
可以先在1到n-1中找到与n不互质的数,然后把他们减掉
比如φ(12)
把12质因数分解,12=2*2*3,其实就是得到了2和3两个质因数
然后把2的倍数和3的倍数都删掉
2的倍数:2,4,6,8,10,12
3的倍数:3,6,9,12
本来想直接用12 - 12/2 - 12/3
但是6和12重复减了
所以还要把即是2的倍数又是3的倍数的数加回来 (>﹏<)
所以这样写12 - 12/2 - 12/3 + 12/(2*3)
这叫什么,这叫容斥啊,容斥定理听过吧
比如φ(30),30 = 2*3*5
所以φ(30) = 30 - 30/2 - 30/3 - 30/5 + 30/(2*3) + 30/(2*5) + 30/(3*5) - 30/(2*3*5)
但是容斥写起来好麻烦( ̄. ̄)
有一种简单的方法
φ(12) = 12*(1 - 1/2)*(1 - 1/3) = 12*(1 - 1/2 - 1/3 + 1/6)
φ(30) = 30*(1 - 1/2)*(1 - 1/3)*(1 - 1/5) = 30*(1 - 1/2 - 1/3 - 1/5 + 1/6 + 1/10 + 1/15 - 1/30)
你看( •̀∀•́ ),拆开后发现它帮你自动帮你容斥好
所以φ(30)的计算方法就是先找30的质因数
分别是2,3,5
然后用30* 1/2 * 2/3 * 4/5就搞定了
顺便一提,phi(1) = 1
代码如下:
1 //欧拉函数 2 int phi(int x){ 3 int ans = x; 4 for(int i = 2; i*i <= x; i++){ 5 if(x % i == 0){ 6 ans = ans / i * (i-1); 7 while(x % i == 0) x /= i; 8 } 9 } 10 if(x > 1) ans = ans / x * (x-1); 11 return ans; 12 }
(phi就是φ的读音)
机智的代码,机智的我(。・`ω´・)
这个的复杂度是O(√n),如果要你求n个数的欧拉函数,复杂度是O(n√n),这也太慢了
有更快的方法
跟埃筛素数差不多
1 #include<cstdio> 2 const int N = 100000 + 5; 3 int phi[N]; 4 void Euler(){ 5 phi[1] = 1; 6 for(int i = 2; i < N; i ++){ 7 if(!phi[i]){ 8 for(int j = i; j < N; j += i){ 9 if(!phi[j]) phi[j] = j; 10 phi[j] = phi[j] / i * (i-1); 11 } 12 } 13 } 14 } 15 int main(){ 16 Euler(); 17 }
(Euler就是欧拉)
另一种,比上面更快的方法
需要用到如下性质
p为质数
1. phi(p)=p-1 因为质数p除了1以外的因数只有p,故1至p的整数只有p与p不互质
2. 如果i mod p = 0, 那么 phi(i * p)=phi(i) * p (我不会证明)
3.若i mod p ≠0, 那么 phi( i * p )=phi(i) * ( p-1 ) (我不会证明)
(所以我说我会证明都是骗人的╮( ̄▽ ̄)╭)
代码如下:
1 #include<cstdio> 2 using namespace std; 3 const int N = 1e6+10 ; 4 int phi[N], prime[N]; 5 int tot;//tot计数,表示prime[N]中有多少质数 6 void Euler(){ 7 phi[1] = 1; 8 for(int i = 2; i < N; i ++){ 9 if(!phi[i]){ 10 phi[i] = i-1; 11 prime[tot ++] = i; 12 } 13 for(int j = 0; j < tot && 1ll*i*prime[j] < N; j ++){ 14 if(i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j]-1); 15 else{ 16 phi[i * prime[j] ] = phi[i] * prime[j]; 17 break; 18 } 19 } 20 } 21 } 22 23 int main(){ 24 Euler(); 25 }
最后说下
a^b % p 不等价 (a%p)^(b%p) % p
因为
a^φ(p) ≡ 1 (mod p)
所以
a^b % p = (a%p)^(b%φ(p)) % p
(欧拉函数前提是a和p互质)
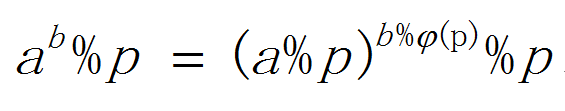
如果p是质数
直接用这个公式
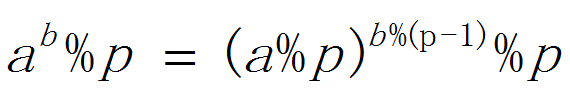
机智的代码,机智的我(。・`ω´・)
///////////////////////////////////////////////
2016年7月23号
我的天哪,我又发现了一个新公式,貌似可以摆脱a和p互质的束缚,让我们来命名为:超欧拉取模进化公式
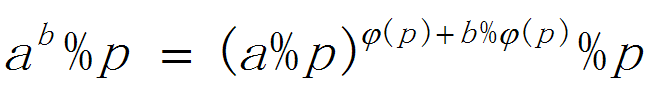
这是历史性的一刻,妈妈再也不用为a和p不互质而担心了= =
#include<cstdio> int phi[100100],prime[30000];//nprime[100100]; int n,len; int main() { int i,j; n=50; phi[1]=1; //nprime[1]=1; for(i=2;i<=n;i++) { //if(!nprime[i]) if(!phi[i]) { prime[++len]=i; phi[i]=i-1; } //printf("%d: ",i); for(j=1;j<=len&&i*prime[j]<=n;j++) { //nprime[i*prime[j]]=1; //printf("%d ",i*prime[j]); if(i%prime[j]==0) { phi[i*prime[j]]=phi[i]*prime[j]; break; } else phi[i*prime[j]]=phi[i]*(prime[j]-1); } //puts(""); } return 0; }
显然以上方法是线性的。
还有一个不需要这个性质的方法,复杂度$O(nloglogn)$。就是根据定义,对于每个质数x(未被其他数更新过欧拉函数值),去更新所有其倍数的欧拉函数值(就是乘上(x-1)再除以x)。
for(i=2;i<=n;i++) if(!phi[i]) for(j=i;j<=n;j+=i) { if(!phi[j]) phi[j]=j; phi[j]=phi[j]/i*(i-1); //i和i-1必定互质,因此保证正确,这样避免乘法溢出 }
欧拉函数的一些性质&欧拉定理:http://www.cnblogs.com/handsomecui/p/4755455.html
欧拉定理做法就是当a,p互质时,$a^{φ(p)}{equiv}1(mod\,p)$,那么$a^{φ(p)-1}$就是a关于模p的乘法逆元。可以用快速幂算。
奇怪的东西:http://blog.csdn.net/qq_36808030/article/details/76687103
当p为质数时即为费马小定理。此时$φ(p)=p-1$,$a^{φ(p)}{equiv}a^{p-1}{equiv}1(mod\,p)$,那么$a^{p-2}$就是a关于模p的乘法逆元
3.线性递推1-n关于模M的乘法逆元
inv[i]表示i的乘法逆元。
设$t=M/i$,$k=M%i$
可得$M=i*t+k$
那么$-i*t{equiv}k(mod\,M)$
由于$inv[i]*inv[k]{equiv}inv[i]*inv[k](mod\,M)$
逐项相乘得$-i*inv[i]*t*inv[k]{equiv}inv[i]*k*inv[k](mod\,M)$
(不知道为什么同余式找不到两边同时乘相同数仍然成立的性质...)
可得$-t*inv[k]{equiv}inv[i](mod\,M)$
即$-(M/i)*inv[M\%i]{equiv}inv[i]$
那么,$inv[i]$可以等于$-(M/i)*inv[M\%i]$。
如果$-(M/i)*inv[M\%i]$为负,则不方便计算。
改成$(M-M/i)*inv[M\%i]\%m$就能保证是最小的可能的正整数。
(http://www.cnblogs.com/dupengcheng/p/5493401.html)
这儿还有个证明(未仔细看):http://blog.csdn.net/yukizzz/article/details/51105009
还有个:http://blog.miskcoo.com/2014/09/linear-find-all-invert
另:
有一个在求解一切除法取模问题(不用互质)时都可以采用的方法:
在求解除法取模问题$(a/b)\%m$时,我们可以转化为$(a \% (b * m))/b$。
来道模板
1.
1 //O2卡过 2 #pragma GCC optimize(2) 3 #pragma GCC diagnostic error "-std=gnu++14" 4 #include<cstdio> 5 #include<cmath> 6 #include<algorithm> 7 using namespace std; 8 namespace fastIO{ 9 #define BUF_SIZE 100005 10 #define OUT_SIZE 100005 11 #define ll long long 12 //fread->read 13 bool IOerror=0; 14 inline char nc(){ 15 static char buf[BUF_SIZE],*p1=buf+BUF_SIZE,*pend=buf+BUF_SIZE; 16 if (p1==pend){ 17 p1=buf; pend=buf+fread(buf,1,BUF_SIZE,stdin); 18 if (pend==p1){IOerror=1;return -1;} 19 //{printf("IO error! ");system("pause");for (;;);exit(0);} 20 } 21 return *p1++; 22 } 23 inline bool blank(char ch){return ch==' '||ch==' '||ch==' '||ch==' ';} 24 inline void read(int &x){ 25 bool sign=0; char ch=nc(); x=0; 26 for (;blank(ch);ch=nc()); 27 if (IOerror)return; 28 if (ch=='-')sign=1,ch=nc(); 29 for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0'; 30 if (sign)x=-x; 31 } 32 inline void read(ll &x){ 33 bool sign=0; char ch=nc(); x=0; 34 for (;blank(ch);ch=nc()); 35 if (IOerror)return; 36 if (ch=='-')sign=1,ch=nc(); 37 for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0'; 38 if (sign)x=-x; 39 } 40 inline void read(double &x){ 41 bool sign=0; char ch=nc(); x=0; 42 for (;blank(ch);ch=nc()); 43 if (IOerror)return; 44 if (ch=='-')sign=1,ch=nc(); 45 for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0'; 46 if (ch=='.'){ 47 double tmp=1; ch=nc(); 48 for (;ch>='0'&&ch<='9';ch=nc())tmp/=10.0,x+=tmp*(ch-'0'); 49 } 50 if (sign)x=-x; 51 } 52 inline void read(char *s){ 53 char ch=nc(); 54 for (;blank(ch);ch=nc()); 55 if (IOerror)return; 56 for (;!blank(ch)&&!IOerror;ch=nc())*s++=ch; 57 *s=0; 58 } 59 inline void read(char &c){ 60 for (c=nc();blank(c);c=nc()); 61 if (IOerror){c=-1;return;} 62 } 63 //getchar->read 64 inline void read1(int &x){ 65 char ch;int bo=0;x=0; 66 for (ch=getchar();ch<'0'||ch>'9';ch=getchar())if (ch=='-')bo=1; 67 for (;ch>='0'&&ch<='9';x=x*10+ch-'0',ch=getchar()); 68 if (bo)x=-x; 69 } 70 inline void read1(ll &x){ 71 char ch;int bo=0;x=0; 72 for (ch=getchar();ch<'0'||ch>'9';ch=getchar())if (ch=='-')bo=1; 73 for (;ch>='0'&&ch<='9';x=x*10+ch-'0',ch=getchar()); 74 if (bo)x=-x; 75 } 76 inline void read1(double &x){ 77 char ch;int bo=0;x=0; 78 for (ch=getchar();ch<'0'||ch>'9';ch=getchar())if (ch=='-')bo=1; 79 for (;ch>='0'&&ch<='9';x=x*10+ch-'0',ch=getchar()); 80 if (ch=='.'){ 81 double tmp=1; 82 for (ch=getchar();ch>='0'&&ch<='9';tmp/=10.0,x+=tmp*(ch-'0'),ch=getchar()); 83 } 84 if (bo)x=-x; 85 } 86 inline void read1(char *s){ 87 char ch=getchar(); 88 for (;blank(ch);ch=getchar()); 89 for (;!blank(ch);ch=getchar())*s++=ch; 90 *s=0; 91 } 92 inline void read1(char &c){for (c=getchar();blank(c);c=getchar());} 93 //scanf->read 94 inline void read2(int &x){scanf("%d",&x);} 95 inline void read2(ll &x){ 96 //#ifdef _WIN32 97 // scanf("%I64d",&x); 98 //#else 99 //#ifdef __linux 100 scanf("%lld",&x); 101 //#else 102 // puts("error:can??t recognize the system!"); 103 //#endif 104 //#endif 105 } 106 inline void read2(double &x){scanf("%lf",&x);} 107 inline void read2(char *s){scanf("%s",s);} 108 inline void read2(char &c){scanf(" %c",&c);} 109 inline void readln2(char *s){gets(s);} 110 //fwrite->write 111 struct Ostream_fwrite{ 112 char *buf,*p1,*pend; 113 Ostream_fwrite(){buf=new char[BUF_SIZE];p1=buf;pend=buf+BUF_SIZE;} 114 void out(char ch){ 115 if (p1==pend){ 116 fwrite(buf,1,BUF_SIZE,stdout);p1=buf; 117 } 118 *p1++=ch; 119 } 120 void print(int x){ 121 static char s[15],*s1;s1=s; 122 if (!x)*s1++='0';if (x<0)out('-'),x=-x; 123 while(x)*s1++=x%10+'0',x/=10; 124 while(s1--!=s)out(*s1); 125 } 126 void println(int x){ 127 static char s[15],*s1;s1=s; 128 if (!x)*s1++='0';if (x<0)out('-'),x=-x; 129 while(x)*s1++=x%10+'0',x/=10; 130 while(s1--!=s)out(*s1); out(' '); 131 } 132 void print(ll x){ 133 static char s[25],*s1;s1=s; 134 if (!x)*s1++='0';if (x<0)out('-'),x=-x; 135 while(x)*s1++=x%10+'0',x/=10; 136 while(s1--!=s)out(*s1); 137 } 138 void println(ll x){ 139 static char s[25],*s1;s1=s; 140 if (!x)*s1++='0';if (x<0)out('-'),x=-x; 141 while(x)*s1++=x%10+'0',x/=10; 142 while(s1--!=s)out(*s1); out(' '); 143 } 144 void print(double x,unsigned int y){ 145 static ll mul[]={1,10,100,1000,10000,100000,1000000,10000000,100000000, 146 1000000000,10000000000LL,100000000000LL,1000000000000LL,10000000000000LL, 147 100000000000000LL,1000000000000000LL,10000000000000000LL,100000000000000000LL}; 148 if (x<-1e-12)out('-'),x=-x;x*=mul[y]; 149 ll x1=(ll)floor(x); if (x-floor(x)>=0.5)++x1; 150 ll x2=x1/mul[y],x3=x1-x2*mul[y]; print(x2); 151 if (y>0){out('.'); for (size_t i=1;i<y&&x3*mul[i]<mul[y];out('0'),++i); print(x3);} 152 } 153 void println(double x,int y){print(x,y);out(' ');} 154 void print(char *s){while (*s)out(*s++);} 155 void println(char *s){while (*s)out(*s++);out(' ');} 156 void flush(){if (p1!=buf){fwrite(buf,1,p1-buf,stdout);p1=buf;}} 157 ~Ostream_fwrite(){flush();} 158 }Ostream; 159 inline void print(int x){Ostream.print(x);} 160 inline void println(int x){Ostream.println(x);} 161 inline void print(char x){Ostream.out(x);} 162 inline void println(char x){Ostream.out(x);Ostream.out(' ');} 163 inline void print(ll x){Ostream.print(x);} 164 inline void println(ll x){Ostream.println(x);} 165 inline void print(double x,int y){Ostream.print(x,y);} 166 inline void println(double x,int y){Ostream.println(x,y);} 167 inline void print(char *s){Ostream.print(s);} 168 inline void println(char *s){Ostream.println(s);} 169 inline void println(){Ostream.out(' ');} 170 inline void flush(){Ostream.flush();} 171 //puts->write 172 char Out[OUT_SIZE],*o=Out; 173 inline void print1(int x){ 174 static char buf[15]; 175 char *p1=buf;if (!x)*p1++='0';if (x<0)*o++='-',x=-x; 176 while(x)*p1++=x%10+'0',x/=10; 177 while(p1--!=buf)*o++=*p1; 178 } 179 inline void println1(int x){print1(x);*o++=' ';} 180 inline void print1(ll x){ 181 static char buf[25]; 182 char *p1=buf;if (!x)*p1++='0';if (x<0)*o++='-',x=-x; 183 while(x)*p1++=x%10+'0',x/=10; 184 while(p1--!=buf)*o++=*p1; 185 } 186 inline void println1(ll x){print1(x);*o++=' ';} 187 inline void print1(char c){*o++=c;} 188 inline void println1(char c){*o++=c;*o++=' ';} 189 inline void print1(char *s){while (*s)*o++=*s++;} 190 inline void println1(char *s){print1(s);*o++=' ';} 191 inline void println1(){*o++=' ';} 192 inline void flush1(){if (o!=Out){if (*(o-1)==' ')*--o=0;puts(Out);}} 193 struct puts_write{ 194 ~puts_write(){flush1();} 195 }_puts; 196 inline void print2(int x){printf("%d",x);} 197 inline void println2(int x){printf("%d ",x);} 198 inline void print2(char x){printf("%c",x);} 199 inline void println2(char x){printf("%c ",x);} 200 inline void print2(ll x){ 201 //#ifdef _WIN32 202 // printf("%I64d",x); 203 //#else 204 //#ifdef __linux 205 printf("%lld",x); 206 //#else 207 // puts("error:can't recognize the system!"); 208 //#endif 209 //#endif 210 } 211 inline void println2(ll x){print2(x);printf(" ");} 212 inline void println2(){printf(" ");} 213 #undef ll 214 #undef OUT_SIZE 215 #undef BUF_SIZE 216 }; 217 using namespace fastIO; 218 typedef long long LL; 219 LL x,y; 220 LL a,b,n; 221 LL exgcd(LL a,LL b) 222 { 223 if(b==0) 224 { 225 x=1;y=0; 226 return a; 227 } 228 else 229 { 230 LL t1=exgcd(b,a%b),t=x; 231 x=y; 232 y=t-a/b*y; 233 return t1; 234 } 235 } 236 int main() 237 { 238 read(n);read(b); 239 for(a=1;a<=n;a++) 240 if(exgcd(a,b)==1) 241 { 242 LL t1=floor(-(double)x/b)+1; 243 println(t1*b+x); 244 } 245 return 0; 246 }
2.
1 //O2也救不了我 2 #pragma GCC optimize(2) 3 #include<cstdio> 4 typedef long long LL; 5 LL n,p; 6 LL poww(LL a,LL b) 7 { 8 LL base=a,ans=1; 9 while(b) 10 { 11 if(b&1) ans=(ans*base)%p; 12 b>>=1; 13 base=(base*base)%p; 14 } 15 return ans; 16 } 17 int main() 18 { 19 LL i; 20 scanf("%lld%lld",&n,&p); 21 for(i=1;i<=n;i++) 22 printf("%lld ",poww(i,p-2)); 23 return 0; 24 }
3.
1 #include<cstdio> 2 typedef long long LL; 3 LL inv[3001000],n,p; 4 int main() 5 { 6 LL i; 7 scanf("%lld%lld",&n,&p); 8 inv[1]=1; 9 printf("%lld ",inv[1]); 10 for(i=2;i<=n;i++) 11 { 12 inv[i]=(p-p/i)*inv[p%i]%p; 13 printf("%lld ",inv[i]); 14 } 15 return 0; 16 }
