常见排序算法

索引

1. 插入排序 
    1.1 直接插入 
    1.2 折半插入 
    1.3 希尔排序 
2. 交换排序 
    2.1 冒泡排序 
    2.2 快速排序 
3. 选择排序 
    3.1 直接选择 
    3.2 堆排序 
4. 归并排序  
    4.1 迭代归并  
总结

1. 插入排序

    思想：每步将一个待排序的对象, 按其排序码大小, 插入到前面已经排好序的一组对象的适当位置上, 直到对象全部插入为止。

1.1 直接插入

    1.1.1 方法： 
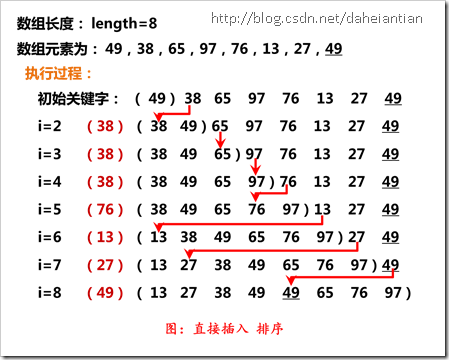
        当插入第i (i >= 1) 个对象时, 前面的V[0], V[1], …, V[i-1]已经排好序。这时, 用V[i]的排序码依次与V[i-1], V[i-2], …的排序码顺序进行比较, 找到插入位置即将V[i]插入, 原来位置上的对象向后顺移。 
      具体过程： 
        1. 把n个待排序的元素看成为一个“有序表”和一个“无序表”； 
        2. 开始时“有序表”中只包含1个元素，“无序表”中包含有n-1个元素； 
        3. 排序过程中每次从“无序表”中取出第一个元素，依次与“有序表”元素的关键字进行比较，将该元素插入到“有序表”中的适当位置，有序表个数增加1，直到“有序表”包括所有元素。

    1.1.2 实例图：

    

1.1.3 代码：

/**
 * 直接插入排序：将数组从小到大排序
 */
#include <iostream>
using namespace std;

typedef int Index;//下标的别名
typedef int Type;//待排序的数组的元素类型

/**
 * 直接插入排序
 */
void direct_insert_sort(Type *array, int length) {
    Index i;
    Index j;//插入的位置
    Type temp;

    for(i=1; i<length; i++) {//i=1，即从第二个元素开始（第一个元素下标为0）
        temp = array[i];
        j=i;
        while(j>0 && array[j-1]>temp) {
            array[j] = array[j-1];
            j--;
        }
        //如果i!=j，说明要插入到前面的“已续表”中
        if(i!=j){
            array[j] = temp;
        }
    }
}

int main(int argc, char **argv) {
    Type array[19] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9};//待排序的数组
    shell_sort(array, 19);

    //排序后，输出数组
    for(int i=0; i<19; i++) {
        cout<<array[i]<<"  ";
    }
    cout<<endl;

    return 0;
}

     1.1.4 分析： 
        时间复杂度：O(n^2)； 稳定的。 
        在下面两种情况，直接插入排序的效率较高：①序列中元素很少；②序列中的元素已经基本有序。

1.2 折半插入

    1.2.1 方法： 
        在“直接插入排序”中，将在“有序表”中查找符合要求的项，利用二分查找完成。

    1.2.2 实例图： 
        和“直接插入排序”排序过程相同。（两者只是“查找插入位置的方法”不同）

    1.2.3 代码： 

/**
 * 折半插入排序
 */
void binary_insert_sort(Type *array, int length) {
    Index i;
    Index k;
    Index left, right;//二分查找时记录左右两侧的下标
    Type temp;
    
    for(i=1; i<length; i++) {
        left = 0;
        right = i-1;//查找时，不包括第i个，因为是要将第i个插入到合适的位置
        temp = array[i];
        while(left<=right) {
            Index middle = (left+right)/2;
            if( array[middle]<=temp ){ //注意：当middle==temp时，要是left加1。否则，算法将“不稳定”
                left = middle+1;
            }else{
                right = middle-1;
            }
        }
        for(k=i; k>left; k--){
            array[k] = array[k-1];
        }
        array[left] = temp;
    }
}

int main(int argc, char **argv) {
    Type array[19] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9};//待排序的数组
    shell_sort(array, 19);

    //排序后，输出数组
    for(int i=0; i<19; i++) {
        cout<<array[i]<<"  ";
    }
    cout<<endl;

    return 0;
}

    1.2.4 分析： 
        时间复杂度：O(N*logN)； 稳定的（注意若处于后面“无序表”中的项，若等于前面“有序表”中的项，要将该项插入到“有序表”中对应项的后面）。 
        相对于“直接插入排序”：比较次数比“直接插入排序”的最差情况要好得多，但是比“直接插入排序”的最好情况要差，尤其是当数组已经排好序或者接近有序的时候。也就是说，“折半插入排序”不是在所有情况都优于“直接插入排序”。

1.3 希尔排序（缩小增量排序）

    1.3.1 方法： 
        因为在“直接插入排序”过程中，若元素已经基本有序，那么“直接插入排序”的效率较高。引出了“希尔排序”的基本思想： 
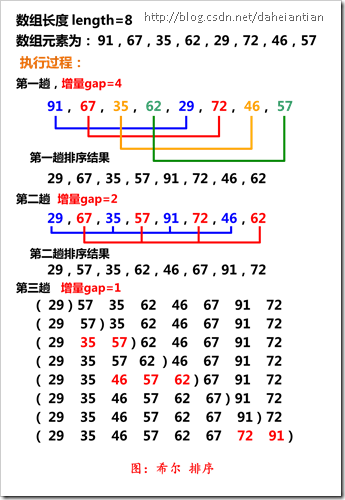
        1. 设待排序的序列有 n 个对象，首先取一个整数 gap < n 作为间隔, 将下标相差为gap的倍数对象放在一组。 
        2. 在组内作 直接插入排序。 
        3. 然后逐渐缩小间隔 gap, 例如取 gap = gap/2，重复上述的组划分和排序工作。直到最后取 gap == 1, 将所有对象放在同一个组中进行排序为止。

    1.3.2 实例图：

    1.3.3 代码：

/**
 * 希尔排序：将数组从小到大排序
 */
#include <iostream>
using namespace std;

typedef int Index;//下标的别名
typedef int Type;//待排序的数组的元素类型

/**
 * 希尔排序
 */
void shell_sort(Type *array, int length) {
    Index i;
    Index j;//插入的位置
    Type temp;
    int gap = length/2;//子序列间隔，这里取长度的一半

    while(gap!=0) {
        for(i=gap; i<length; i+=gap) { //1. i从gap开始取值；2. i每次递增gap
            temp = array[i];
            j=i;
            while(j>=gap && array[j-gap]>temp) {
                array[j] = array[j-gap];
                j -= gap;
            }
            //如果i!=j，说明要插入到前面的“已续表”中
            if(i!=j) {
                array[j] = temp;
            }
        }
        gap /= 2;
    }
}

int main(int argc, char **argv) {
    Type array[19] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9};//待排序的数组
    shell_sort(array, 19);

    //排序后，输出数组
    for(int i=0; i<19; i++) {
        cout<<array[i]<<"  ";
    }
    cout<<endl;

    return 0;
}

    1.3.4 分析： 
         时间复杂度：n^1.25 ~ 1.6*n^1.25之间（统计资料），是不稳定的；gap的取值会影响希尔排序的效率。

2. 交换排序

    思想：两两比较待排序对象的排序码,如果发生逆序，则进行交换。直到所有对象都排好序为止。

2.1 冒泡排序

    2.1.1 方法： 
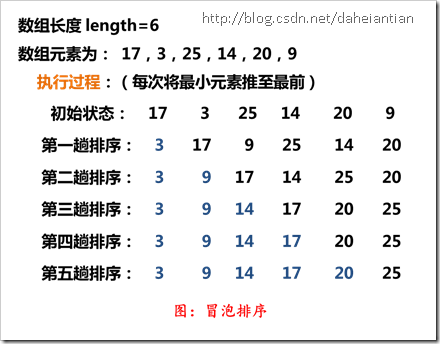
        1. 对待排序序列从前向后（从下标较大的元素开始）依次比较相邻元素的关键字，若发现逆序则交换； 
        2. 使较小的元素逐渐前移（或者较大的元素逐渐后移）；（假定按照“从小到大”排序）  
      改进措施：  
          如果一趟比较下来没有进行过交换，就说明序列已经有序；可以通过设置一个标志exchange记录一趟遍历中是否进行了交换。

    2.1.2 实例图： 

    2.1.3 代码：

/**
 * 冒泡排序：将数组从小到大排序
 */
#include <iostream>
using namespace std;

typedef int Index;//下标的别名
typedef int Type;//待排序的数组的元素类型

/*
 * 方法一：每次将最小的元素推至前端
 */
void bubble_sort1(Type *array, int length) {
    Index i, j;
    bool exchange;//标志一次遍历中，是否进行了交换

    for(i=0; i<length-1; i++) {
        exchange = false;//每次循环开始时，值为false
        for(j=length-1; j>i; j--) {
            if(array[j]<array[j-1]) { //两两比较，当两者相等时，不交换，这样才能使该排序稳定，即原来在前面的排序后也在前面
                exchange = true;

                Type temp = array[j-1];
                array[j-1] = array[j];
                array[j] = temp;
            }
        }
        //如果本次循环没有交换，说明数组已经排序完毕
        if(!exchange) {
            break;
        }
    }
}
/*
 * 方法二：每次将最大的元素推至末尾
 */
void bubble_sort2(Type *array, int length) {
    Index i, j;
    bool exchange;//标志一次遍历中，是否进行了交换

    for(i=0; i<length-1; i++) {
        exchange = false;//每次循环开始时，值为false
        for(j=0; j<length-i-1; j++) {
            if(array[j]>array[j+1]) { //两两比较，和“将较小元素推至前端”相同，当两者相等时，不交换，这样才能使该排序稳定，即原来在后面的排序后也在后面
                exchange = true;

                Type temp = array[j+1];
                array[j+1] = array[j];
                array[j] = temp;
            }
        }
        //如果本次循环没有交换，说明数组已经排序完毕
        if(!exchange) {
            break;
        }
    }
}

int main(int argc, char **argv) {
    Type array[19] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9};//待排序的数组
    bubble_sort1(array, 19);

    //排序后，输出数组
    for(int i=0; i<19; i++) {
        cout<<array[i]<<"  ";
    }
    cout<<endl;

    return 0;
}

    2.1.4 分析： 
        时间复杂度：O(n^2)； 稳定的。

2.2 快速排序

    2.2.1 方法：  
        “冒泡排序”中，元素的比较是从一端到另一端进行，每次移动一个位置；如果要是能“从两端到中间”进行，比“基准元素”大的一次就能交换到后面单元，比“基准元素”小的一次就能交换到前面单元，每次移动的距离较远，从而总的比较次数和移动次数都会减少。 
        步骤：（利用分治的算法思想） 
            1. 任取待排序序列中的某个元素作为基准（一般取第一个元素）； 
            2. 通过一趟排序，将待排元素分为左右两个子序列： 
                  左子序列元素的关键字均小于或等于基准元素的关键字； 
                  右子序列的关键字则大于基准元素的关键字； 
            3. 分别对两个子序列继续进行排序，重复以上步骤，直至整个序列有序。（是一个递归的过程）

    2.2.2 实例图：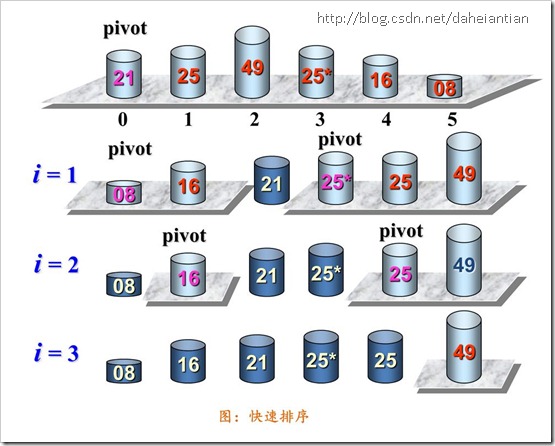 

         当 i 为1时，执行过程为：

 
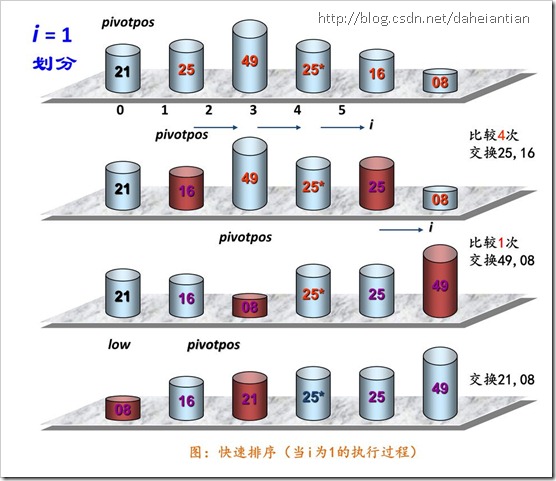
    2.2.3 代码：   

/**
 * 快速排序：将数组从小到大排序
 */
#include <iostream>
using namespace std;

typedef int Index;//下标的别名
typedef int Type;//待排序的数组的元素类型

void quick_sort_recursion(Type *array, Index left, Index right);
int partition(Type *array, Index left, Index right);

/**
 * 快速排序，接口，内部调用“递归实现函数”quick_sort_recursion
 */
void quick_sort(Type *array, int length) {
    quick_sort_recursion(array, 0, length-1);
}
/**
 * 快速排序，递归实现函数
 */
void quick_sort_recursion(Type *array, Index left, Index right) {
    if(left<right) {
        int pivot_index = partition(array, left, right);//获得基准位置
        quick_sort_recursion(array, left, pivot_index-1);//递归调用，将子序列排序，注意不包括pivot_index位置的元素
        quick_sort_recursion(array, pivot_index+1, right);
    }
    /*
     调用这里的left和right都是有效的下标。如果类似C++ STL中，right是末尾的下一位，应写为下面的形式：
      原则：①调用partition函数的参数都是有效的；②调用自身quick_sort_recursion的参数right是末尾的下一个；  
     if(left<right) {
        int pivot_index = partition(array, left, right-1);//使用right-1
        quick_sort_recursion(array, left, pivot_index);//使用pivot_index
        quick_sort_recursion(array, pivot_index+1, right);
    }
     相应的，在quick_sort函数中的调用形式应修改为：quick_sort_recursion(array, 0, length);
     */
}
/**
 * 利用第一元素作为基准元素，将整个序列划分为两个部分。
 * 步骤：
 *   1. 比基准元素小的都移动到左侧，比基准元素大的都移动到右侧，变量pivot_position始终记录着比基准元素小的元素的最后一个元素。
 *   2. 最后将基准元素（第一个）与pivot_position位置上的元素交换，就可以达到目的。
 * 这时基准元素所在的位置也就是最终排序完成后，应该在的位置
 * 注意：这个实现中，参数中的left和right都是有效的，特别注意的是，这里的right是序列最后一个元素的下标，不是最后一个元素的下一个。
 */
int partition(Type *array, Index left, Index right) {
    Type pivot = array[left];//基准元素值
    Index pivot_index = left; //记录已比较的元素中，比基准元素小的元素的最后一个位置；也是最后要返回的位置

    Index i;
    for(i=left+1; i<=right; i++) {//这里 i 能够等于right，就要求传给partition的参数中的right参数，一定要是有效的
        if(array[i]<pivot) {
            pivot_index++;
            //交换array[pivot_index]和array[i]
            if(i!=pivot_index) {
                Type temp = array[i];
                array[i] = array[pivot_index];
                array[pivot_index] = temp;
            }
        }
    }
    //交换基准元素（第一个元素）和array[pivot_index]
    array[left] = array[pivot_index];
    array[pivot_index] = pivot;
    return pivot_index;
}

#define ARRAY_LENGTH 18

int main(int argc, char **argv) {
    Type array[ARRAY_LENGTH] = { 5, 4, 3, 2, 1, 0, 0, 1, 2, 3, 4, 5, 5, 4, 3, 2, 1, 0};//待排序的数组
    //调用接口函数
    quick_sort(array, ARRAY_LENGTH);

    //排序后，输出数组
    for(int i=0; i<ARRAY_LENGTH; i++) {
        cout<<array[i]<<"  ";
    }
    cout<<endl;

    //调用递归实现函数
    quick_sort_recursion(array, 0,ARRAY_LENGTH);
    //排序后，输出数组
    for(int i=0; i<ARRAY_LENGTH; i++) {
        cout<<array[i]<<"  ";
    }
    cout<<endl;

    return 0;
}

    2.2.4 分析： 
        快速排序是一个“递归算法”，快速排序的趟数等于递归树的高度。         时间复杂度：最好 O(N*logN)；最差 O(N^2)； 
        空间复杂度：最好 O(logN)； 最差 O(N)； 
        是一种不稳定的算法。但是当序列元素数量较多时，快速排序的效率一般很好，所以经常采用；但是当元素较少时，其比一般方法可能要慢（因为要递归）。

3. 选择排序

    思想：每一趟遍历，都从序列中找到最小的元素，将其放到队列的开始位置。或者找到序列的最大元素，放到队列的末尾。

3.1 直接选择排序

    3.1.1 方法： 
        1. 在一组对象 V[i]～V[n-1] 中选择最小的对象； 
        2. 将它与这组对象中的第一个对象对调; 
        3. 在剩下的对象V[i+1]～V[n-1]中重复执行第①、②步, 直到剩余对象只有一个为止。 

    3.1.2 实例图：     

/**
 * 直接选择排序：将数组从小到大排序
 */
#include <iostream>
using namespace std;

typedef int Index;//下标的别名
typedef int Type;//待排序的数组的元素类型

/**
 * 直接选择排序，每次选取最小的替换到开头
 */
void direct_select_sort(Type *array, int length) {
    Index i, j;
    Index min_index;//每趟循环中，最小元素的下标
    Type temp;
    for(i=0; i<length-1; i++) {// i 的取值范围是从0到length-2，不包括最后一个元素（下标为 length-1），因为只剩一个元素时不需要判断
        min_index = i;
        for(j=i+1; j<length; j++) {//从i+1开始
            if(array[j]<array[min_index]) {
                min_index = j;
            }
        }
        temp = array[i];
        array[i] = array[min_index];
        array[min_index] = temp;
    }
}

#define ARRAY_LENGTH 18

int main(int argc, char **argv) {
    Type array[ARRAY_LENGTH] = { 5, 4, 3, 2, 1, 0, 0, 1, 2, 3, 4, 5, 5, 4, 3, 2, 1, 0};//待排序的数组
    direct_select_sort(array, ARRAY_LENGTH);

    //排序后，输出数组
    for(int i=0; i<ARRAY_LENGTH; i++) {
        cout<<array[i]<<"  ";
    }
    cout<<endl;

    return 0;
}

    3.1.4 分析： 
        时间复杂度：O(n^2)。不稳定。 
        总的比较次数固定为：n*(n-1)/2次，即O(n^2)级别。

3.2 堆排序

    3.2.1 方法：  
        1. 根据初始输入数据，利用堆的“下滤调整算法”形成初始最大堆； 
        2. 将最大元素换到最后一个元素，对前面的元素构建最大堆。 
        3. 重复执行以上两步，直到所有元素排序完成。

    3.2.2 实例图： 

    

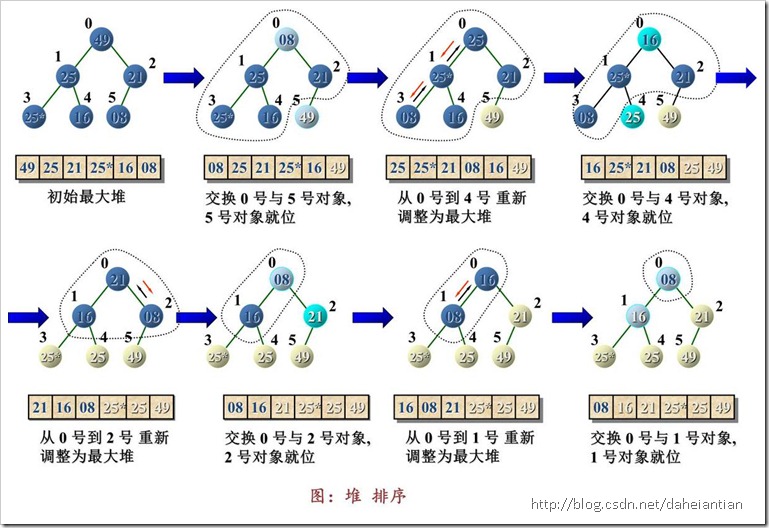
3.2.3 代码：

/**
 * 堆排序：将数组从小到大排序
 *  方法：依次建立最大堆，将堆顶元素（最大元素）与最后一个元素交换；
 */
#include <iostream>
using namespace std;

typedef int Index;//下标的别名
typedef int Type;//待排序的数组的元素类型

void filter_down(Type *heap, Index pos, int length);
void build_heap(Type *array, int length);
void heap_sort(Type *array, int length);

/**
 * 堆的下滤操作
 */
void filter_down(Type *heap, Index pos, int length) {
    Index current=pos;//记录下滤过程中的当前节点
    Index child = 2*pos+1;//当前节点的子节点，当下标从0开始时，找到左孩子的下标
    
    Type temp = heap[pos];
    
    while(child<length) {
        //若左右孩子都存在，找到左右孩子中最大的那个
        if(child+1<length && heap[child]<heap[child+1]) {
            ++child;
        }
        //如果当前节点小于 其 孩子，将“子节点的值”赋给“当前节点”
        if(temp<heap[child]) {
            heap[current] = heap[child];
        } else {
            break;
        }
        current = child;
        child = 2*child + 1;
    }
    heap[current] = temp;
}
/**
 * 建立 堆
 */
void build_heap(Type *array, int length) {
    Index i;
    for(i=(length-2)/2; i>=0; i--) {
        filter_down(array, i, length);
    }
}

/**
 * 堆排序
 */
void heap_sort(Type *array, int length) {
    //建立堆
    build_heap(array, length);
    
    Index i;
    Type temp;
    for(i=length-1; i>0; i--) {// i 的范围从length-1 到 1，共length-2次循环（不包括i=0），若只剩一个元素，则说明整个序列已经有序了。
        //交换
        temp = array[0];
        array[0] = array[i];
        array[i] = temp;
        //下滤
        filter_down(array, 0, i);
    }
}

#define ARRAY_LENGTH 18

int main(int argc, char **argv) {
    Type array[ARRAY_LENGTH] = { 5, 4, 3, 2, 1, 0, 0, 1, 2, 3, 4, 5, 5, 4, 3, 2, 1, 0};//待排序的数组

    heap_sort(array, ARRAY_LENGTH);

    //排序后，输出数组
    for(int i=0; i<ARRAY_LENGTH; i++) {
        cout<<array[i]<<"  ";
    }
    cout<<endl;

    return 0;
}

   3.2.4 分析： 
        时间复杂度：O(n*logn)； 
        空间复杂度：O(1)； 
        不稳定。

4. 归并排序  

    思想：将两个或两个以上的“有序表”合并成一个新的“有序表”。

4.1迭代归并

   4.1.1 方法：  
        利用“两路归并”过程进行，步骤如下： 
            1. 把序列看成是 n 个长度为 1 的有序子序列 (归并项)，先做两两归并，得到 n / 2 个长度为 2 的归并项 (如果 n 为奇数，则最后一个有序子序列的长度为1)； 
            2. 然后看成长度为2, 4, 8……的有序子序列，两两归并，直到得到长度为n的有序序列； 
      注意： 
         如果n不是2len的整数倍, 则一趟归并到最后,可能遇到两种情形： 
             1. 剩下一个长度为len的归并项和另一个长度不足len的归并项, 可用merge算法将它们归并成一个长度小于 2len 的归并项； 
             2. 只剩下一个归并项，其长度小于或等于 len, 将它直接抄到目标序列中。

    4.1.2 实例图： 

     

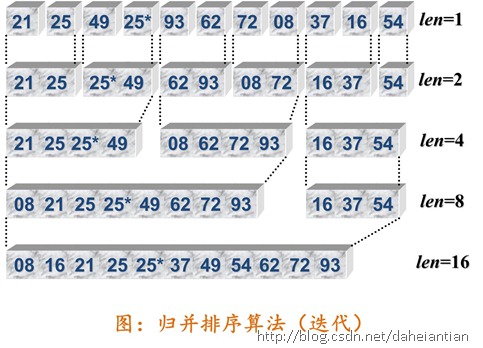
4.1.3 代码： 

/**
 * 归并排序（迭代实现）：将数组从小到大排序
 */
#include <iostream>
using namespace std;

typedef int Index;//下标的别名
typedef int Type;//待排序的数组的元素类型

void merge(Type *src, Type *dest, Index left, Index middle, Index right);
void merge_pass(Type *src, Type *dest, int section, int length);
void merge_sort(Type *array, int length);

/**
 * 合并两个列表
 * 将src中[left, middle]位置，和src中[middle+1, right]开始位置的元素合并到dest中
 *  注意：上面的区间是闭区间
 */
void merge(Type *src, Type *dest, Index left, Index middle, Index right) {
    Index i = left; //在src的[left, middle]中前进
    Index j = middle+1; //在src的[middle+1, right]中前进
    Index k = left; //在dest中前进
    while(i<=middle && j<=right) {
        if(src[i]<=src[j]) { //注意：因为src[i]在前面，为了是算法稳定，当src[i]==src[j]时，应先添加stc[i]
            dest[k++] = src[i++];
        } else {
            dest[k++] = src[j++];
        }
    }
    //[left, middle]还没有走完
    while(i<=middle) {
        dest[k++] = src[i++];
    }
    //[middle+1, right]还没有走完
    while(j<=right) {
        dest[k++] = src[j++];
    }
}
/**
 * 归并排序的具体执行函数
 */
void merge_pass(Type *src, Type *dest, int section, int length) {
    Index i=0;
    //1. 合并开始部分
    while(i+2*section <= length) {//因为序列下标从0开始，有等号
        merge(src, dest, i, i+section-1, i+2*section-1);
        i += 2*section;
    }
    //2.剩余部分有两块
    if(i+section<length) {
        merge(src, dest, i, i+section-1, length-1);
    } else {
        //3. 只剩一部分，直接添加到末尾
        while(i<length) {//这里没有等号
            dest[i] = src[i];
            i++;
        }
    }
}

/**
 * 归并排序
 */
void merge_sort(Type *array, int length) {
    int section = 1;//小部分的长度
    Type *help_array = new Type[length];//辅助数组
    while(section<length) { //section不需要等于length
        //从array归并到help_array
        merge_pass(array, help_array, section, length);
        section *= 2;
        //从help_array归并到array
        merge_pass(help_array, array, section, length);
        section *= 2;
    }
    delete []help_array;
}

#define ARRAY_LENGTH 18

int main(int argc, char **argv) {
    Type array[ARRAY_LENGTH] = { 5, 4, 3, 2, 1, 0, 0, 1, 2, 3, 4, 5, 5, 4, 3, 2, 1, 0};//待排序的数组
    merge_sort(array, ARRAY_LENGTH);

    //排序后，输出数组
    for(int i=0; i<ARRAY_LENGTH; i++) {
        cout<<array[i]<<"  ";
    }
    cout<<endl;

    return 0;
}

    4.1.4 分析： 
        时间复杂度：O(N*logN)； 
        空间复杂度：一个和原来数组一样大小的数组，O(N)； 
        该算法是稳定的。

5. 总结

排 序 方 法	比较次数		移动次数		稳定性	附加存储
	最好	最差	最好	最差		最好	最差
直接插入排序	n	n^2	0	n^2	Ö	1
折半插入排序	n logn		0	n^2	Ö	1
起泡排序	n	n^2	0	n^2	Ö	1
快速排序	nlogn	n^2	< nlogn	n^2	´	logn	n
直接选择排序	n^2		0	n	´	1
堆排序	n logn		n logn		´	1
归并排序	n logn		n logn		Ö	n