对数据进行一定的操作时,数据有序会使其处理起来方便很多,对数据的排序方法有很多种,而因为我们经常需要对数据多次排序或者对很大的数据量进行排序,不同排序算法花费时间不同。简单介绍几种排序算法;
一、简单排序算法:冒泡排序、插入排序,选择排序;
二、快速排序算法:基本快速排序、三数取中快速排序、三划分快速排序;
三、合并排序
四、线性时间排序算法:计数排序、桶排序
实现的冒泡排序、插入排序、基本快速排序、合并排序,对快速排序以及合并排序写下个人的理解。
快速排序(平均时间nlogn):
选定一个基准值a[i](即partition过程,使得i左侧都比a[i]小,i右侧都比a[i]大,也确定了a[i]的位置),然后通过递归过程,对a[l:i-1]和a[i+1,r]进行排序,同时对这两个子序列排序又是同一类问题,最后就在经过多次的选基准值并确定其位置,就对数列排好序了。图解: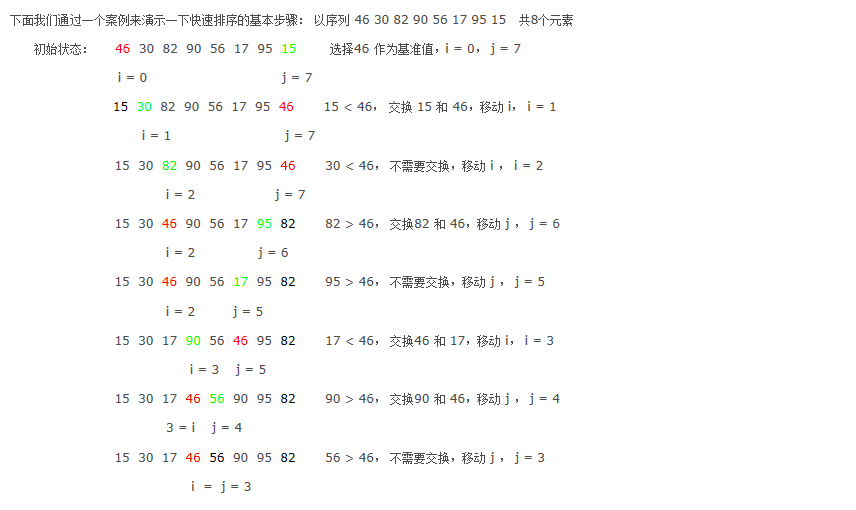
合并排序(平均时间nlogn):
分治的思想,将数列分为两个大小相等的子数列分别排序,子序列排序又是将子序列分为两个子序列分别排序,最后最基础的就是两个元素进行分,一大一小,然后通过一个辅助数组b,将两边已经分好的序列从前往后挑小的放到b里面,最后一定有一半被挑完,另一半还剩下一些元素(还是排好序的,但比b中的所有元素都大),然后再将这些元素加到b中,最后将b再复制回原来分成两个子数列的a数列中。一个递归的思想;
图解: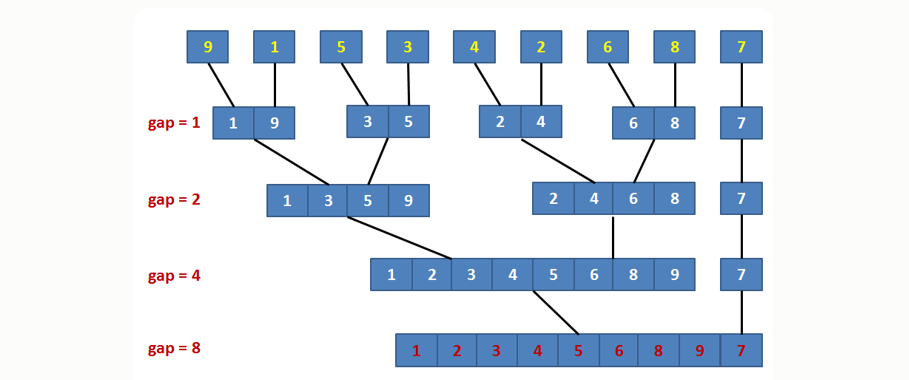
略说三数取中快排:大致思想就是在用递归处理时,如果数组的规模比较小,比如5~25之间,就可以通过非递归算法实现,比如插入排序,可以有效提高性能,就在quicksort()函数的前面加一个判断此时数组规模if(r-l>10)insertion();
略说三划分快排:基本思想是在数组a[l:r]中存在大量键值相同的元素时,可以提高效率;v=a[r]为基准值,将数组分为a[l:i],a[i+1,j-1],a[j,r]三段,左段键值小于v,中段等于v,右段大于v,算法对左右两段数组进行递归排序;
实现代码:
#include<cstdio>
#include<cstdlib>
#include<algorithm>
int b[100005];
void swap(int *a,int *b)
{
int tmp=*a;
*a=*b;
*b=tmp;
}
//冒泡排序(选择排序,我分不太清二者的区别) ,复杂度无论如何都是O(n2)量级;
//最坏(任何)情况下需要执行n(n-1)/2次元素比较;
void bubble(int a[],int l,int r)
{
int i,j;
for(i=l;i<r;i++)
{
for(j=i+1;j<=r;j++) //即每次将(除前面已找出的更小的数)最小的数字找出,放在数组前段;
{
if(a[i]>a[j])
{
swap(&a[i],&a[j]);
}
}
}
}
//插入排序,在如果是一串有序的数字输入时,插入排序的复杂度可以减小甚至变成O(n)量级;
//最坏情况下 ,需要执行n(n-1)/2次比较和交换;
void insert(int a[],int l,int i)
{
int v=a[i];
while(i>l&&v<a[i-1]) //可以理解为对冒泡排序优化的地方是,不再是不管这个数和要比较的数大小关系如何都做循环,
//而通过while添加判断大小关系的条件决定是否做循环,如果给的是一个有序的数组,则复杂度就可以优化到O(n)量级;
{
a[i]=a[i-1];
i--;
}
a[i]=v;
}
void insertion(int a[],int l,int r)
{
int i,j;
for(i=l+1;i<=r;i++)insert(a,l,i);
}
//快速排序,是基于分治思想的排序算法
int partition(int a[],int l,int r) //以一个确定的基准元素a[r]对子数组a[l:r]进行划分,左边比a[i]小等,右边比a[i]大等,这个是算法的关键
{
int p=a[l];
while(l<r)
{
while(l<r&&a[r]>=p)r--;
a[l]=a[r];
while(l<r&&a[l]<=p)l++;
a[r]=a[l];
}
a[l]=p;
return l;
} //partition的计算时间显然是O(r-l-1);在最好的情况之下,是每次划分都产生两个大小为n/2的区域,则T(n)=O(nlogn);
void quicksort(int a[],int l,int r) //对含有n个元素a[0:n-1]进行快速排序只要调用quicksort(a,0,n-1);即可
{
int i;
if(r<=l)return;
i=partition(a,l,r); //以一个确定的基准元素a[r]对子数组a[l:r]进行划分,左边比a[i]小等,右边比a[i]大等,这个是算法的关键
quicksort(a,l,i-1);
quicksort(a,i+1,r);
}
//合并排序,基于分治思想对n个元素进行排序;
void mergeB(int a[],int l,int m,int r)
{
int i=l,j=m+1,p=m,q=r;
int k=0;
while(i<=p&&j<=r) //对前后两个有序的数列整合在一起,每次比较两个数列中的值,将更小的放进辅助数组b中,选择的数组游标向下移;
{
if(a[i]<=a[j])
b[k++]=a[i++];
else
b[k++]=a[j++];
}
while(i<=p) //最后要么剩下前面的有序数列,要么剩下后面的有序数列,将剩下的加入辅助数组就完成了对整个数列的整合;
b[k++]=a[i++];
while(j<=q)
b[k++]=a[j++];
for(i=0;i<k;i++) //将辅助数列b复制回原数组a中;
a[l+i]=b[i];
}
void mergesort(int a[],int l,int r)
{
int m=(r+l)/2; //取中点
if(r<=l)return;
mergesort(a,l,m); //对左半端进行排序
mergesort(a,m+1,r); //对右半段进行排序
mergeB(a,l,m,r); //合并到数组b中
}
//堆排序
void HeapAdjust(int* a,int i,int size)
{
int lchild=2*i;int rchild=2*i+1; //左儿子节点为2*i,右儿子节点为2*i+1;
int max=i; //max为临时辅助变量游标;
if(i<=size/2)
{
if(lchild<=size&&a[lchild]<a[max])max=lchild;
if(rchild<=size&&a[rchild]<a[max])max=rchild;
if(max!=i)
{
swap(&a[max],&a[i]); //将max作为父节点,即根据大小交换父子节点;
HeapAdjust(a,max,size); //防止调整之后以max作为父节点的子树不是堆;
}
}
}
void BuildHeap(int* a,int size) //建立堆;
{
int i;
for(i=size/2;i>=1;i--) //非叶节点的最大序号值为size/2;
{
HeapAdjust(a,i,size); //对每一个非叶节点进行调整判断大小关系;
}
}
void HeapSort(int* a,int size) //将堆一次一次提取出当前的最大值,也就可以解决第k小的数的问题;
{
int i;
BuildHeap(a,size); //建堆
for(i=size;i>=1;i--)
{
swap(&a[1],&a[i]); //即对一个已经建好的大顶堆,每次都将堆顶a[1]放到最后,即和a[i]交换,也就存储了第k大的元素值;
HeapAdjust(a,1,i-1); //每次将目前的最大值放到后面之后(交换之后,堆顶变成原来的最后的值,对需要调整)都要对堆检查是否还是一个堆;
}
}
int main()
{
int i,j,n;
int a[]={0,10,9,6,8,15,4,27,5,4,16};
// bubble(a,0,9);
// insertion(a,0,9);
// quicksort(a,0,9);
// mergesort(a,0,9);
HeapSort(a,11); //堆排序一般是从数组编号为1开始存储,所以在对a数组改动了(a数组前加了一个0)以便堆排序输出;
for(i=0;i<11;i++)
printf("%d%c",a[i],i==10?'
':' ');
return 0;
}
第五次作业:
1、(将一串1~n的无序数列排序过程中,每个数能到的最右端与最左端差值的最大值,即计算每个数左边比之大的数的个数和右边比它小的数的个数)容易知道虽然题目说的是冒泡排序,但是计算每个数其前后有多少个比之大和小的数的个数,在合并排序的过程中就可以计算,每次合并过程都对数的大小进行了比较,记录其个数即可。题目博客链接
代码:
#include<stdio.h>
#include<stdlib.h>
const int N = 100007;
int a[N], wz[N], you[N], tmp[N];
int min(int &a, int &b) {
return a<b ? a : b;
}
void msort(int l, int mid, int r) {
int i = l, j = mid + 1, p = l;
while (i <= mid&&j <= r) {
if (a[i]<a[j]) {
tmp[p++] = a[i];
you[a[i]] += j - mid - 1; ++i;
}
else {
tmp[p++] = a[j++];
}
}
while (i <= mid) {
tmp[p++] = a[i];
you[a[i]] += r - mid; ++i;
}
while (j <= r)tmp[p++] = a[j++];
for (i = l; i <= r; i++)a[i] = tmp[i];
}
void guibing(int l, int r) {
if (l == r)return;
int mid = (l + r) >> 1;
guibing(l, mid);
guibing(mid + 1, r);
msort(l, mid, r);
return;
}
int main() {
int n, i;
scanf("%d", &n);
for (i = 1; i <= n; i++) {
scanf("%d", &a[i]);
wz[a[i]] = i;
}
guibing(1, n);
for (i = 1; i <= n; i++) {
printf("%d ", wz[i] + you[i] - min(wz[i], i));
}puts("");
}
2、(将一个丢失序列(丢失数据为0),和已知可能是丢失数据的数列合并,看是否能够合并成功使之单调递增)可以借助一个数组储存0的位置,然后对要插入的数列先排序,再插入之后进行比较就可以得到结果;题目博客链接
欠缺:还一个第k小元素问题没有深入学习,之后补上之后予以更新;
补充:
已经对第k小(大)元素的问题学习,即通过堆排序的方式实现;代码已更新;堆排序图解: