Partial Order Pruning: for Best Speed/Accuracy Trade-off in Neural Architecture Search

CVPR 2019文章

 

github地址：https://github.com/lixincn2015/Partial-Order-Pruning

 

    目前大多数设计高精度网络结构的工作通常采用FLOP来评估网络的复杂度。但是仅仅FLOP指标不能真正决定实际的推理速度。比如说，在硬件和软件高度优化的Nvidia GPU上，3x3的卷积的FLOPs是1x1卷积的9倍，但是速度上却不是9倍。另外一个决定推理速度的是内存的访问（ memory access）。而且，考虑到硬件和软件的多样性，我们无法找出同一个网络结构在所有的平台上都是最优的。

 

    在实际真实的场景中，部署深度神经网络时，在目标平台上达到一个速度与精度的平衡是非常重要的。然而目前大多数现有的自动结构搜索只关注于高精度。在本文中，我们提出一个较好的速度与精度折中的搜索出来的网络，称为“ Partial Order Pruning”。

 

　It prunes the architecture search space with a partial order assumption to automatically search for the architectures with the best speed and accuracy trade-off. Our algorithm explicitly takes profile information about the inference speed on the target platform into consideration.

 

    本文目标是回答两个问题：

• 给定最大可接受的延迟（ latency）下，我们可以达到的最高精度是什么？
• 符合确定的精度要求下，我们可以期望的最低推理延迟是多少？

 

    本文的贡献：

• 我们是第一批研究网络结构搜索的速度和精度平衡问题的人。通过对搜索空间进行偏序剪枝（Partial Order），我们的“偏序剪枝”可以有效地提高搜索速度和精度的权衡。
• 我们提出了若干种在嵌入式设备TX2上达到高精度和快推理速度的DF网络。在ImageNet验证集上，我们的DF1和DF2A网络的准确率超过了ResNet18/50，并且推理延迟分别降低了43%和39%。
• 我们将提出的算法应用于搜索一个分割网络的解码器架构。使用DF主干网络，我们在GPU端和嵌入式端TX2上都达到了实时并且state-of-the-art的效果。在GTX 1080Ti上，DF1-Seg网络在2014*2048的分辨率下，达到106.4FPS，mIoU 74.1%的效果；在TX2上，DF1-Seg网络在1280*720（720p）的分辨率下达到21.8FPS。

搜索空间（Search Space）

 

本文在搜索空间（search space）中提供一个通用的网络架构，如下图Figure2.

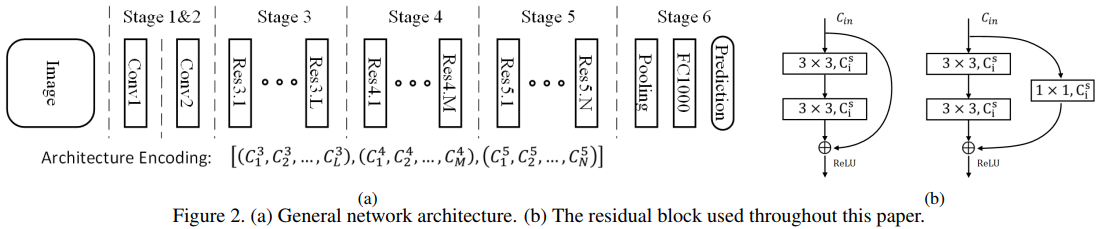
 这个通用的网络结构包含6个stage，stage1~5中各自有一个stride=2的下采样，stage6使用一个全局平局池化（ global average pooling）和全连接层来得到最终的预测结构。stage1和2负责在大分辨率下提取低层的特征，但是这部分的计算量比较大。由于我们是要得到一个搞笑的网络，因此我们在stage1和2中只使用1个卷积层，如Conv1和Conv2，我们发现这种情况下也可以达到很好的精度。对于stage3,4,5，每个stage依次包含L，M，N个residual block，其中L，M，N是整数。不同的L，M，N，可以得到不同的网络深度。第s个stage的第i个residual block的宽度（即通道数）记为，其中。依照经验，我们设定后面block的宽度需要大于等于前面block的宽度。我们使用的residual block（即与ResNet中的一致）示意图如Figure2（b）所示。如果输入的尺寸与输出的不匹配，那么会加一个额外的投影层（projection layer）。另外，所有卷积层后面跟着batch normalization层和ReLU激活函数。

 

延时估计（Latency Estimation）

    不同的深度（block的数量）和不同的宽度（每个block的通道数）组成了所有可能的结构。这些所有的网络结构的时间分布可能是非常短的时间到正无穷。但是我们只关心延迟在特定范围内（即延时大于Tmin，小于Tmax）的网络结构。我们使用TensorRT库提供的分析器来获取网络层级别的延迟。我们发现一个具有相同配置（如输入输入的尺寸）的block的延迟也是一样的。因此我们构造了查找表，当一个block的输入输出的通道数（ci/co），宽高（hi/wi/ho/wo）确定时，我们就可以得到该block的延时Latency。比如，在TX2上，。

通过简单地总结所有block的延迟，我们可以有效地估计一个网络结构x的延迟Lat(x)。我们选择那些延迟大于Tmin，小于Tmax的网络结构进行下一步分析。

 

偏序假设（Partial Order Assumption）

    偏序（partial order）是定义在一个集合上的二元关系。它意味着集合里某些元素对（x,y），一个元素x先于其他y的排序，用x < y 表示。这里，“partial”表明并不是所有元素对需要具有可比性。

    在本文的搜索空间中的网络结构中也存在这种偏序（partial order）关系。本文网络结构中的偏序关系如下图Figure 4所示。

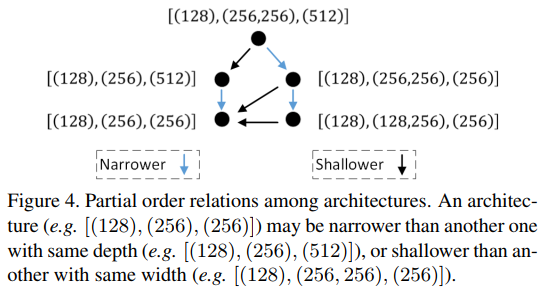
    如果x与y的宽度相同，但是x比y更浅（ shallower），或者如果x与y深度相同，但是x比y更窄（ narrower），那么借助上述的理论，我们就可以说在顺序上x在y的前面，记为x<y。

    网络结构x的准确率和延迟分别用Acc(x)和Lat(x)表示，那么当x < y时，有

上述公式（1）假设在顺序上当x在y的前面时，x的准确率和延迟均低于y。这个假设可能对非常深的网络（如具体上百层的网络）不成立，但是本文中由于使用的是小网络，作者实验后是满足上述假设的。 

 

Partial Order Pruning

    本文的网络结构搜索算法的目标是：在每一个非常小的延迟范围[T, T +  δt]内，找出最高准确率的那个网络结构。

其中， δt是一个很短的时间范围，比如是0.1ms。

 

本文搜索算法如下：

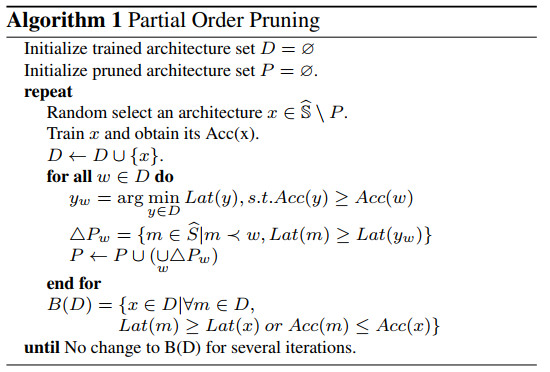
其中，表示延迟在[Tmin, Tmax]之间的网络结构集合。

 

这部分的细节请查看原始paper。

 

实验部分

本文在 Nvidia Jetson TX2和GTX 1080Ti这两个硬件平台上进行实验。

 

作者训练了200多个网络，实验结果如下图Figure 7所示。在整体训练结束后，取出两个限制条件下最优的结构重新训练，获得最高精度，即下图中的DF1和DF2。将DF2中的basic block替换成bottleneck block后，即为网络DF2A。

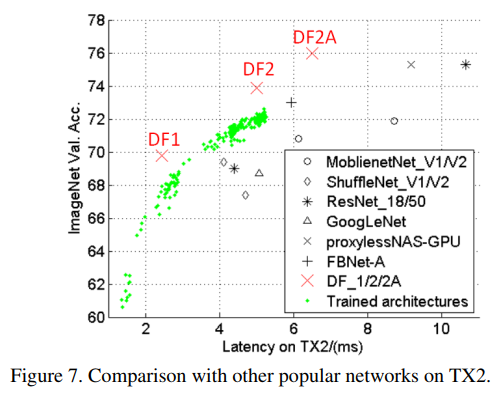
本文搜索出来的DF系列的网络结构如下：

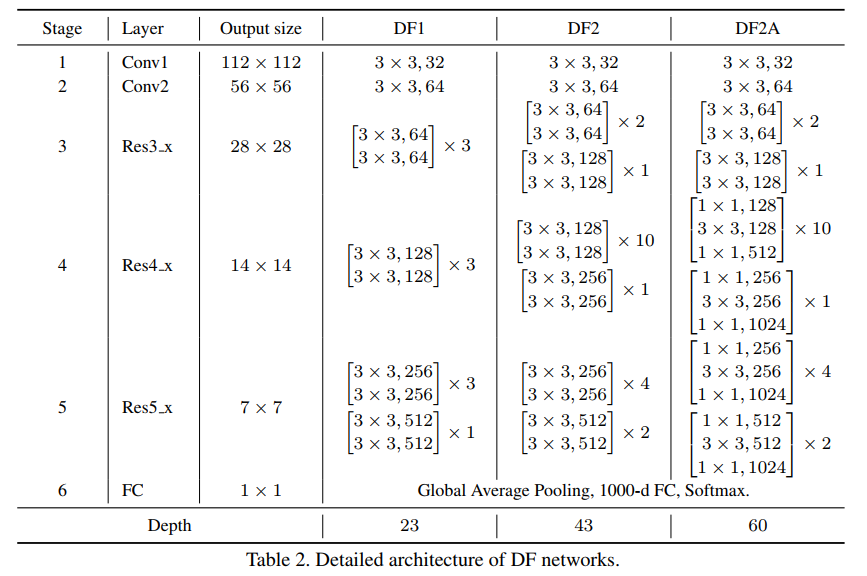
 下面的Table1表格展示了本文搜索出来的网络与热门网络的对比。

从上面的表格中可以看出：

• 相比于ResNet-18和GoogLeNet，DF1准确率高了69.8%，但是推理时间比前者分别少了43%和51%；
• DF2与ResNet-18和GoogLeNet相比，推理时间差不多，但是准确率高了4.9%和5.2%。
• DF2A比ResNet-50精度高一些，推荐时间也快了不少。
• 相比于MobileNet和ShuffleNet网络，这两个网络虽然FLOPs低，但是这两个网络得出推理时间却比本文提出的DF1要长。这是因为这两个网络具有更高的内存访问消耗（ memory access cost）。这说明仅仅FLOPs并不能决定实际在具体运行平台上的推理速度。
• 相比于其他采用NAS方法得到的模型，如NASNet和PNASNet，这两个模型的具有很高的延迟；相比于FBNet和ProxylessNAS，虽然这两个模型在搜索时也将平台相关因素考虑在内，但是延迟仍然比DF网络高，DF网络具有更好的速度/精度的折中。这是因此（a）DF网络是专门在TX2平台搜索得到的；（b）FBNet和ProxylessNAS使用了 inverted bottleneck模块，这个模型会带来更高的内存访问消耗。（c）FBNet和ProxylessNAS的目标是寻找更好的构建块的架构，但是我们更注重平衡整体架构的宽度和深度。

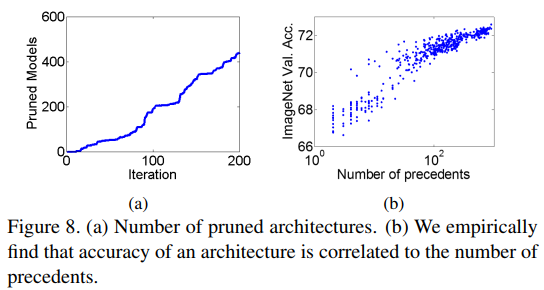
基于我们搜索结果，我们观察到如下几点：

• 在早期阶段采用非常快的下采样，可以获得更高的效率。因此我们在第1和第2阶段都只使用了一个卷积层，而且也可以达到一个好的精度。
• 带下采样的卷积层比池化层更好一些，可以得到更高的精度。我们最终只在网络的最后使用1个全局平均池化层（ global average pooling）
• 如Figure8(b)可以看出，一个网络的前序越多，其精度也越高，也会有一个更好的深度与宽度的平衡。