『高性能模型』卷积复杂度以及Inception系列

转载自知乎：卷积神经网络的复杂度分析

之前的Inception学习博客：

『TensorFlow』读书笔记_Inception_V3_上

『TensorFlow』读书笔记_Inception_V3_下

一、时间复杂度

即模型的运算次数，可用FLOPs衡量，也就是浮点运算次数（FLoating-point OPerations）。

单个卷积层的时间复杂度

　　　　　　Time~O(M²·K²·C_in·C_out)

M：输出特征图边长

K：卷积核尺寸

C：通道数目

输出边长M计算公式为：

　　　　　　M = (X - K + 2*Padding)//Stride + 1

• 注1：为了简化表达式中的变量个数，这里统一假设输入和卷积核的形状都是正方形
• 注2：严格来讲每层应该还包含 1 个 参数，这里为了简洁就省略了
• 注3：TensorFlow中SAME形式输出为(X/Stride)上取整，因为TF中默认总共填充K/2，注意不需要进行2*Padding

下图展示了单个Cout的上单个点的计算示意，需要重复计算：C_out·每张输出特征图上像素数次。

卷积神经网络整体复杂度

　　　　　　Time~O(∑_l=1 M²·K²·C_l-1·C_l)

l表示层编号，实质就是对各个层求和。

卷积层实现可以很好的看清实现机理：out层、out长宽、in层循环，循环体内k²级别运算：

def conv2d(img, kernel):
    height, width, in_channels = img.shape
    kernel_height, kernel_width, in_channels, out_channels = kernel.shape
    out_height = height - kernel_height + 1
    out_width = width - kernel_width + 1
    feature_maps = np.zeros(shape=(out_height, out_width, out_channels))
    for oc in range(out_channels):              # Iterate out_channels (# of kernels)
        for h in range(out_height):             # Iterate out_height
            for w in range(out_width):          # Iterate out_width
                for ic in range(in_channels):   # Iterate in_channels
                    patch = img[h: h + kernel_height, w: w + kernel_width, ic]
                    feature_maps[h, w, oc] += np.sum(patch * kernel[:, :, ic, oc])

    return feature_maps

二、空间复杂度

空间复杂度（访存量），严格来讲包括两部分：总参数量 + 各层输出特征图。

• 参数量：模型所有带参数的层的权重参数总量（即模型体积，下式第一个求和表达式）
• 特征：模型在实时运行过程中每层所计算出的输出特征图大小（下式第二个求和表达式）

　　　　　　Space~O(∑K²·C_l-1·C_l + ∑M²·C_l)

M：输出特征图边长

K：卷积核尺寸

C：通道数目

三、复杂度对模型的影响

时间复杂度决定了模型的训练/预测时间。如果复杂度过高，则会导致模型训练和预测耗费大量时间，既无法快速的验证想法和改善模型，也无法做到快速的预测。

空间复杂度决定了模型的参数数量。由于维度诅咒的限制，模型的参数越多，训练模型所需的数据量就越大，而现实生活中的数据集通常不会太大，这会导致模型的训练更容易过拟合。

当我们需要裁剪模型时，由于卷积核的空间尺寸通常已经很小（3x3），而网络的深度又与模型的表征能力紧密相关，不宜过多削减，因此模型裁剪通常最先下手的地方就是通道数。

四、Inception系列优化思路

1、Inception_v1：1*1卷积降维同时优化时间复杂度和空间复杂度

InceptionV1 借鉴了 Network in Network 的思想，在一个 Inception Module 中构造了四个并行的不同尺寸的卷积/池化模块（上图左），有效的提升了网络的宽度。但是这么做也造成了网络的时间和空间复杂度的激增。对策就是添加 1 x 1 卷积（上图右红色模块）将输入通道数先降到一个较低的值，再进行真正的卷积。

在3*3卷积分支上加入64个1*1卷积前后的时间复杂度对比如下式：

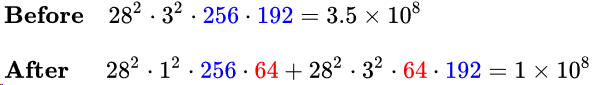
同理，在5*5卷积分支上加入64个1*1卷积前后的时间复杂度对比如下式：

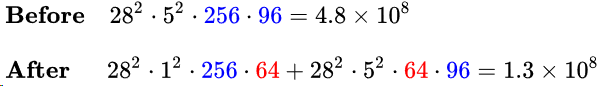
整个层的参数量变化如下：

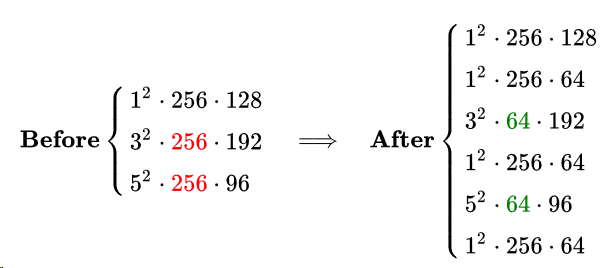
2、Inception_v1：使用GAP（全局平局均池化）代替全连接

全连接层复杂度分析：X*X的输入Flatten为X²的输入，输出神经元个数可以视为1*1*C_out,则：

　　　　　　Time~O(1²·X²·C_in·C_out)

　　　　　　Space~O(X²·C_in·C_out + X²·C_in) ~ O(X²·C_in·C_out)

空间复杂度第一部分为权重参数，第二部分为当前输入大小。顺便一提我之前的一个误区：全连接层相对卷积层其运算瓶颈不在时间复杂度，而在空间复杂度，我之前的印象里把两者混为一谈了。

使用GAP后，首先将C_in·X²的输入转化为C_in，然后1*1卷积为C_out：

　　　　　　Time~O(C_in·C_out)

　　　　　　Space~O(C_in·C_out + C_in）~ O(C_in·C_out)

Space来说可能有点问题：C_in·X²的原输入应该还是要存储的，不过由于不涉及到卷积运算，姑且不细究。

但是注意：GAP会影响收敛速度，不过并不会影响最终的精度。

3、Inception_v2：两个3*3卷积联级替代5*5卷积

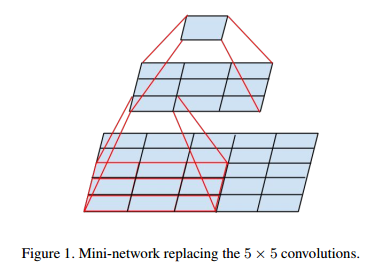
两个3*3卷积联级的感受野与单个5*5卷积相当，计算公式可见『计算机视觉』感受野和anchor，替换后时间复杂度却可降低：

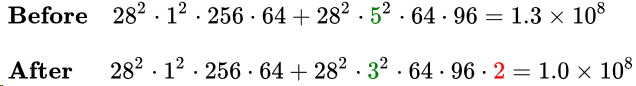
4、Inception_v3：使用N*1和1*N卷积联级代替N*N卷积

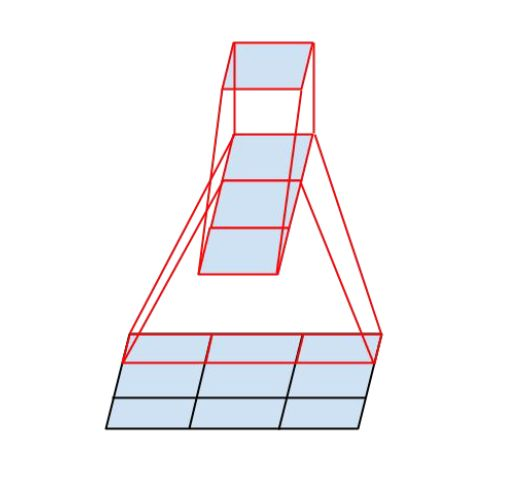
InceptionV3 中提出了卷积的 Factorization，在确保感受野不变的前提下进一步简化，复杂度的改善同理可得，不再赘述。

5、Xnception：使用Depth wise Separable Convolution

Xception 中每个输入通道只会被对应的一个卷积核扫描，降低了模型的冗余度。对于深度可分离卷积Depthwise Separable 是一个 Depthwise conv 加一个 Pointwise conv，其中 Depthwise 是M²·K²·C_in，Pointwise 是M²·C_in·C_out，即：

　　　　　　Time~O(M²·K²·C_in + M²·C_in·C_out)