矩阵左乘向量的两种理解
1,矩阵左乘向量可以理解为对向量进行线性变换
探究原理的话,可以理解左乘为对整个空间(基&目标向量)进行线性变换,其中,
- 变换矩阵是基‘在基的坐标的列向量组合
- 目标向量是向量在基中的坐标
- 结果向量是向量’在基下的坐标
就结果来看,实质是利用向量在基下的坐标和基‘在基下的坐标,求出整个空间旋转到基’位置后向量的新位置(向量‘)在原基下的坐标。
详细说明如下:

把基画出来的原因是因为矩阵变换的其实是基。
举例子来看看,比如旋转(旋转矩阵 ):
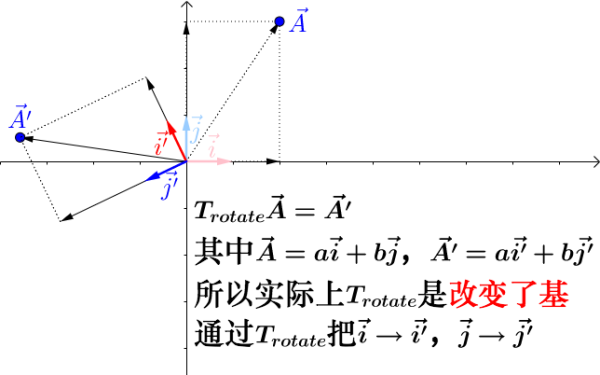

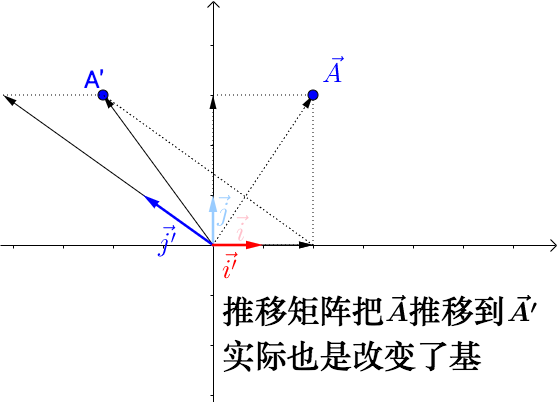
2.矩阵左乘向量可以理解为单纯的对向量进行换基操作
和上面不同的是这个理解中目标向量本身在绝对空间中没有发生任何变化,仅仅是换了对基:
- 变换矩阵是基‘在基下的坐标的列向量组合
- 目标向量是原向量在基’下的坐标
- 结果向量是原向量在基下的坐标
就结果来看,实质上是利用向量在基‘下的坐标和基’在基下的坐标求出向量在基下的坐标。
换基操作详解如下:
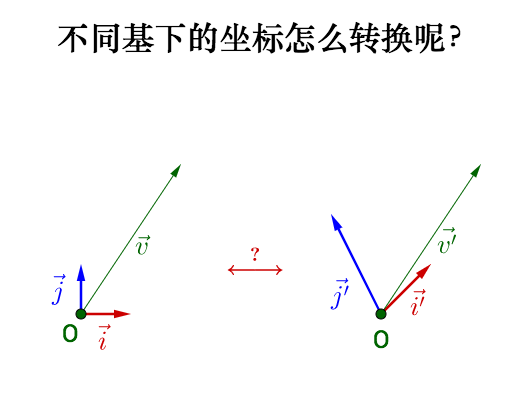

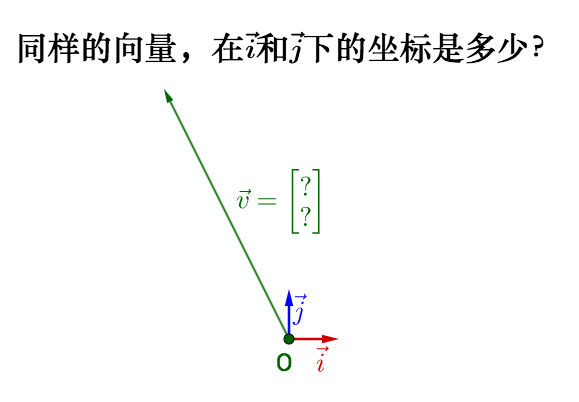

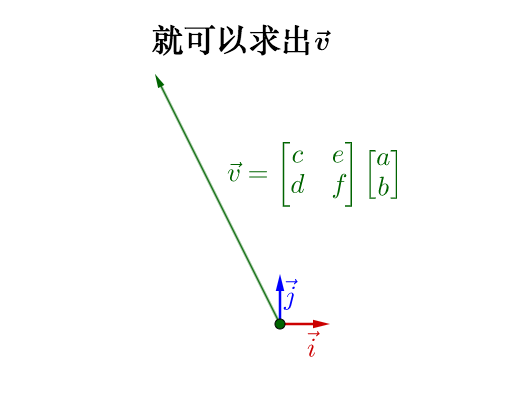

结论参考:
行列式的实质
引用自童哲的回答
1,行列式
2,原来立方体有一个体积
3,行列式
就这么简单?没错,就这么简单。
所以说:行列式的本质就是一句话:
行列式就是线性变换的放大率!
理解了行列式的物理意义,很多性质你根本就瞬间理解到忘不了!!!比如这个重要的行列式乘法性质:
道理很简单,因为放大率是相乘的啊~!
你先进行一个
你把“先进行
然后你要问等式两边是否一定相等,我可以明确告诉你:too simple 必须相等。因为其实只是简单的把事实陈述出来了。这就好像:
“ 你经过股票投资,把1块钱放大3被变成了3块钱,然后经过实业投资,把3块钱中的每一块钱放大5倍成了5块钱。请问你总共的投资放大率是多少?”
翻译成线性代数的表达就是:
这还不够!我来解锁新的体验哈~
上回咱们说到行列式其实就是线性变换的放大率,所以你理解了:
那么很自然,你很轻松就理解了:
so easy,因为
同时你也必须很快能理解了
“矩阵
因为再自然不过了啊,试想
请注意我们这里说的体积都是针对
所以凡是
当然要证明也是小菜一碟轻而易举的:
由
可知
这怎么可能啊~?