『科学计算』贝叶斯公式学习

贝叶斯公式介绍

条件概率和全概率

在介绍贝叶斯定理之前，先简单地介绍一下条件概率，描述的是事件 A 在另一个事件 B 已经发生条件下的概率，记作 ， A 和 B 可能是相互独立的两个事件，也可能不是：

表示 A，B 事件同时发生的概率，如果 A 和 B 是相互独立的两个事件，那么：

上面的推导过程反过来证明了如果 A 和 B 是相互独立的事件，那么事件 A 发生的概率与 B 无关。

稍微做一下改变：

考虑到先验条件 B 的多种可能性，这里引入全概率公式：

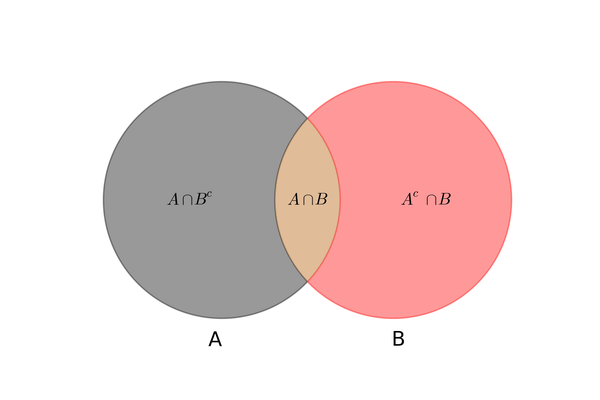
这里 表示事件 B 的互补事件，从集合的角度来说是 B 的补集：

条件概率和全概率公式可以通过韦恩图形象地表示出来：

贝叶斯公式

在条件概率和全概率的基础上，很容易推导出贝叶斯公式：

看上去贝叶斯公式只是把 A 的后验概率转换成了 B 的后验概率 + A 的边缘概率的组合表达形式，因为很多现实问题中 或 很难直接观测，但是 和 却很容易测得，利用贝叶斯公式可以方便我们计算很多实际的概率问题。

贝叶斯过滤器介绍

原文链接

贝叶斯过滤器的使用过程
    现在，我们收到了一封信邮件。在未统计分析之前， 我们假定它是垃圾邮件的概率为50%。（【注释】有研究表明，用户收到的电子邮件中，80%是垃圾邮件。但是，这里仍然假定垃圾邮件的“先验概率”为50%。）
    我们用S表示垃圾邮件（spam），H表示正常邮件（healthy）。因此，P(S)和P(H)的先验概率，均为50%。
    
    然后，对这封邮件进行解析，发现其中包含了sex这个词，请问这封邮件属于垃圾邮件的概率有多高？
    我们用W表示“sex”这个词，那么问题就变成了如何计算P(S|W)的值，即在某个词语（W)已经存在的情况下，垃圾邮件（S）的概率有多大。
    根据条件概率公式，马上可以写出：
    
    因此，这封新邮件是垃圾邮件的概率等于99%。这说明，sex这个词的推断能力很强，将50%的“先验概率”一下子提高到了99%的“后验概率”。

联合概率的计算
    做完上面一步，请问我们能否得出结论，这封新邮件就散垃圾邮件？
    回答是不能。因为一封邮件包含很多词语，一些词语（比如sex）是这是垃圾邮件，另一些说不是。你怎么知道以哪个词为准呢？
    Paul GraHam的做法是：选出这封邮件中P(S|W)最高的15个词，计算它们的联合概率。（【注释】如果有的词是第一次出现，无法计算P(S|W)，Paul Graham就假定这个值等于0.4。因为垃圾邮件用的往往都是某些固定的词语，所以如果你从来没有见过某个词，它多半是一个正常的词。）
    所谓联合概率，就是指在多个事件发生的情况下，另一个事件发生的概率有多大。比如，已知W1和W2是两个不同的词语，它们都出现在某封电子邮件之中，那么这封邮件是垃圾邮件的概率，就是联合概率。
    在已知W1和W2的情况下，无丰就是两种结果：垃圾邮件（事件E1）或正常邮件（事件E2）。
    
    其中，W1、W2和垃圾邮件的概率分别如下：
    
    如果假定所有事件都是独立事件（【注释】严格地说，这个假定不成立，但是这里可以忽略），那么就可以计算P(E1)和P(E2)：
    
    又由于在W1和W2已经发生的情况下，垃圾邮件的概率等于下面的式子：
    
    【关于上面这式子，为什么P = P(E1)/(P(E1)+P(E2))？有如下解释】
    在上面已经说明了，E1是在W1和W2同时出现的情况下垃圾邮件的事件，E2是W1和W2同时出现的情况下正常邮件的事件，注意这里的前提都是“在W1和W2同时出现的情况下”。
    那么，P = P(E1)/(P(E1)+P(E2))，其意思是W1和W2共同出现的情况下是垃圾邮件的概率，而P(W1,W2)实际上就是P(E1)+P(E2)，所以P = P(E1)/(P(E1)+P(E2))。
    【解释完毕】
 
     即
    
    将P(S)等于0.5代入，得到
    
    这就是联合概率的计算公式。如果你不是很理解，点击这里查看更多的解释。

    【感觉推导跳过了几步：来自于评论】
    P(S|W1 W2) = P(W1 W2|S)P(S)/( P(W1 W2| S)P(S) + P(W1 W2|~S)P(~S) )
    W1,W2独立：P(W1 W2) = P(W1)P(W2)，P(W1 W2|S) = P(W1|S)P(W2|S)  (?)
     上式=P(W1|S)P(W2|S)P(S) / (P(W1|S)P(W2|S)P(S) + P(W1|~S)P(W2|~S)P(~S))

    应用贝叶斯原理，将P(Wi|S)用P(S|Wi)表示：
    上式 = (P(S|W1)P(S|W2)P(S) * P(W1)P(W2) / P(S)^2) / ((P(S|W1)P(S|W2)P(S) * P(W1)P(W2) / P(S)^2) + (P(~S|W1)P(~S|W2)P(~S) * P(W1)P(W2) / P(~S)^2))
    在P(S) = P(~S) = 0.5的条件下：
    上式 = P(S|W1)P(S|W2) / (P(S|W1)P(S|W2) + P(~S|W1)P(~S|W2))
            = P1P2 / (P1P2 + (1-P1)(1-P2));

最终的计算公式
    将上面的公式扩展到15个词的情况，就得到了最终的概率计算公式：
    
    一封邮件是不是垃圾邮件，就用这个式子进行计算。这时我们还需要一个用于比较的门槛值。Paul Graham的门槛值是0.9，概率大于0.9，表示15个词联合认定，这封邮件有90%以上的可能属于垃圾邮件；概率小于0.9，就表示是正常邮件。
    有了这个公式以后，一封正常的邮件即使出现了sex这个词，也不会被认定为垃圾邮件了。

贝叶斯垃圾邮件分类器原型机

上面说了，需要取15个垃圾邮件中最多的词计算联合概率密度，实际上由于懒，没有进行这步，所以本程序有两个问题：1，正确率仅有70%左右；2，可能会因为概率值过小在联合概率密度计算部分出现分母为0错误，不过理论上来说（讲道理的话），进行前15个词的排序后应该都能有所改善，而我最近手里还有任务要赶，所以学习了贝叶斯方法目的也就达到了，不精益求精了(逃...

import os
import re
import glob
import numpy as np

def get_filenames():
    # 读取文件名列表
    file_dict = {'train':{'ham':[], 'spam':[]}, 'test':{'ham':[], 'spam':[]}}
    for path in ['train', 'test']:
        files = file_dict[path]
        files['ham'].extend(glob.glob(os.path.join('./',path+'/','ham/*.txt')))
        files['spam'].extend(glob.glob(os.path.join('./',path+'/','spam/*.txt')))
    return file_dict, len(file_dict['train']['ham']), len(file_dict['train']['spam'])

def split_word(file_list, word_dict):
    '''把邮件中的单词切分出来，去重，计数（多少份邮件中含此单词）'''
    for name in file_list:
        # print(name)
        with open(name, 'rb') as f:
            # words = set(f.read().split(' '))
            line = f.read().decode('utf-8', 'ignore')
            words = set(re.findall(r'[a-zA-Z]{2,}',line.strip()))
            for word in words:
                # print(word, word_dict.keys())
                if word in word_dict.keys():
                    word_dict.update({word: (word_dict[word]+1)})
                else :
                    word_dict.update({word: 1})
    # print(word_dict)
    return word_dict

def train(file_dict):
    '''调用切词函数，把统计结果写入文件'''
    word_dict = {'ham': {},'spam': {}}
    split_word(file_dict['train']['ham'][:],word_dict['ham'])
    split_word(file_dict['train']['spam'][:],word_dict['spam'])
    with open('./dict_ham.txt','w',encoding= 'gbk') as f:
        for line in word_dict['ham'].items():
            f.write(line[0] + ' ' + str(line[1]) + '
')
    with open('./dict_spam.txt','w',encoding= 'gbk') as f:
        for line in word_dict['spam'].items():
            f.write(line[0] + ' ' + str(line[1]) + '
')
    print(word_dict['ham'])
    print(word_dict['spam'])

def load_model_data(data_name=['./dict_ham.txt', './dict_spam.txt']):
    '''读取写入文件的数据'''
    word_dict = {'ham': {},'spam': {}}
    with open(data_name[0], 'r') as f:
        for line in f.readlines():
            word_dict['ham'].update({line.split(' ')[0]:int(line.split(' ')[1].strip('
'))})
    with open(data_name[1], 'r') as f:
        for line in f.readlines():
            word_dict['spam'].update({line.split(' ')[0]:int(line.split(' ')[1].strip('
'))})
    return word_dict

def calConditionProb(word,dict,num):
    '''计算类含有目标词的概率'''
    if word in dict.keys():
        if dict[word]>=20:
            return dict[word]/float(num)
        else:
            return 0.4
    else:
        return 0.4

def calBayes(word_list, word_dict, num_ham, num_spam):
    '''贝叶斯方法求后验概率'''
    wordProbList = {}
    for word in word_list:
        pw_n = calConditionProb(word,word_dict['ham'],num_ham)
        pw_s = calConditionProb(word,word_dict['spam'],num_spam)

        if pw_s!=pw_n and (pw_s==0.4 or pw_n==0.4):
            ps_w=0.4
        else:
            ps_w=pw_s/(pw_s+pw_n)

        wordProbList.update({word:ps_w})
    return wordProbList

def calJointProb(wordList):
    '''求联合概率密度'''
    ps_w, pn_w = 1, 1
    for word, p in wordList.items():
        ps_w *= p
        pn_w *= (1-p)
        print(ps_w)
    prob = ps_w / (ps_w + pn_w)
    return  prob

def test_file(file_name, word_dict, num_ham, num_spam):
    with open(file_name,'rb') as f:
        line = f.read().decode('utf-8','ignore')
        words = set(re.findall(r'[a-zA-Z]{2,}',line.strip()))
        wordList = calBayes(words, word_dict, num_ham, num_spam)
        return calJointProb(wordList)


if __name__=='__main__':
    training = False

    file_dict, num_ham, num_spam = get_filenames()
    if training == True:
        train(file_dict)
    word_dict = load_model_data()

    num_t, num_w = 0, 0
    for path in file_dict['test']['ham']:
        if test_file(path,word_dict,num_ham,num_spam) > 0.5:
            num_t += 1
            #print('Right')
        else:
            num_w += 1
            #print('Wrong')
    print(num_t/(num_t + num_w))

 代码学习：

with open(name, 'rb') as f:
            line = f.read().decode('utf-8', 'ignore')

 有时候使用'r'命令读取文件时会出现解码错误，这时候可以把'r'改成'rb'，但是read()时候需要解码，否则后面无法识别str，所以需要加上.decode(编码方式)，这时指定出错时处理方式为'ignore'，就不会报错了