题目大意:
题目链接:https://www.luogu.org/problemnew/show/P4130
一条项链包含 N 个珠子,每个珠子的颜色是 1,2,…,c 中的一种。项链
被固定在一个平板上,平板的某个位置被标记位置 1 ,按顺时针方向其他位置被记为 2,3,…,N。
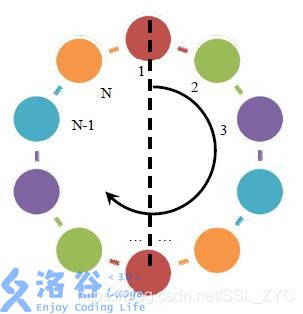
你将要编写的软件系统应支持如下命令:
- 意为。将项链在平板上顺时针旋转k 个位置, 即原来处于位置1 的珠子将转至位置k+1,处于位置2 的珠子将转至位置k+2,依次类推。
- 意为。将平板沿着给定的对称轴翻转,原来处于位置1 的珠子不动,位置2 上的珠子与位置N 上的珠子互换,位置3 上的珠子与位置N-1 上的珠子互换,依次类推。
- 意为。将位置i 上的珠子与位置j 上的珠子互换。
- 意为。将位置i 沿顺时针方向到位置j 的一段染为颜色x。
- 意为。查询当前的项链由多少个“部分”组成,我们称项链中颜色相同的一段为一个“部分”。
- 意为。查询从位置i沿顺时针方向到位置j 的一段中有多少个部分组成。
思路:
这就是那种算法简单思路简单细节贼多的题目
操作3456其实就是线段树的基本操作。维护每个区间左端点的值、右端点的值和这段区间的部分个数即可。
仔细观察发现,操作12都是没有改变这个数列的顺序的。仅仅是改变了位置。所以我们可以通过记录旋转次数以及是否翻转来从询问的点反推回初始的点。这样就可以直接在线段树上维护了。
细节较多,但是实现起来其实不算很难。注意细节即可。
代码不长,也就近200行而已。
代码:
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
using namespace std;
const int N=500010;
int n,m,Q,sum,flag,a[N];
char ch[5];
struct Tree
{
int l,r,lval,rval,cnt,lazy;
}tree[N*4];
int read()
{
int d=0;
char ch_=getchar();
while (!isdigit(ch_)) ch_=getchar();
while (isdigit(ch_))
d=(d<<3)+(d<<1)+ch_-48,ch_=getchar();
return d;
}
void write(int x)
{
if (x>9) write(x/10);
putchar(x%10+48);
}
void up(int x) //利用子节点维护父节点
{
tree[x].cnt=tree[x*2].cnt+tree[x*2+1].cnt;
if (tree[x*2].rval==tree[x*2+1].lval) tree[x].cnt--; //左右相同的连在一起的情况
tree[x].lval=tree[x*2].lval;
tree[x].rval=tree[x*2+1].rval;
}
void pushdown(int x)
{
if (tree[x].lazy) //lazy标记下传
{
tree[x*2].lval=tree[x*2].rval=tree[x*2].lazy=tree[x].lazy;
tree[x*2+1].lval=tree[x*2+1].rval=tree[x*2+1].lazy=tree[x].lazy;
tree[x*2].cnt=tree[x*2+1].cnt=1;
tree[x].lazy=0;
}
}
void build(int x) //建树不解释
{
if (tree[x].l==tree[x].r)
{
tree[x].lval=tree[x].rval=a[tree[x].l];
tree[x].cnt=1;
return;
}
int mid=(tree[x].l+tree[x].r)/2;
tree[x*2].l=tree[x].l;
tree[x*2].r=mid;
tree[x*2+1].l=mid+1;
tree[x*2+1].r=tree[x].r;
build(x*2); build(x*2+1);
up(x);
}
int find(int x,int k) //查询线段树中位置k的值
{
if (tree[x].l==k && tree[x].r==k) return tree[x].lval;
pushdown(x);
int mid=(tree[x].l+tree[x].r)/2;
if (k<=mid) return find(x*2,k);
else return find(x*2+1,k);
}
void change(int x,int k,int val) //单点修改
{
if (tree[x].l==k && tree[x].r==k)
{
tree[x].lval=tree[x].rval=val;
tree[x].cnt=1;
return;
}
pushdown(x);
int mid=(tree[x].l+tree[x].r)/2;
if (k<=mid) change(x*2,k,val);
else change(x*2+1,k,val);
up(x);
}
void Paint(int x,int l,int r,int val) //区间修改
{
if (tree[x].l==l && tree[x].r==r)
{
tree[x].lval=tree[x].rval=tree[x].lazy=val;
tree[x].cnt=1;
return;
}
if (tree[x].l==tree[x].r) return;
pushdown(x);
int mid=(tree[x].l+tree[x].r)/2;
if (r<=mid) Paint(x*2,l,r,val);
else if (l>mid) Paint(x*2+1,l,r,val);
else
{
Paint(x*2,l,mid,val);
Paint(x*2+1,mid+1,r,val);
}
up(x);
}
void Swap(int x,int y)
{
int t1=find(1,x),t2=find(1,y);
change(1,y,t1); change(1,x,t2); //将两者的值交换
}
int ask(int x,int l,int r) //查询l~r中的段落个数
{
if (tree[x].l==l && tree[x].r==r) return tree[x].cnt;
pushdown(x);
int mid=(tree[x].l+tree[x].r)/2;
if (r<=mid) return ask(x*2,l,r);
if (l>mid) return ask(x*2+1,l,r);
int ans=ask(x*2,l,mid)+ask(x*2+1,mid+1,r);
if (tree[x*2].rval==tree[x*2+1].lval) ans--; //左右是相同的,连在一起是一个块
return ans;
}
int get() //转移回去
{
int x;
x=read();
if (flag) x=n-x+2; //有翻转
return ((x-sum)%n+2*n-1)%n+1;
}
int main()
{
n=read(); m=read();
for (int i=1;i<=n;i++)
a[i]=read();
tree[1].l=1; tree[1].r=n;
build(1);
int x,y,k;
Q=read();
while (Q--) //下面都是细节问题,注意就行了
{
scanf("%s",ch);
if (ch[0]=='R')
{
k=read();
if (flag) sum-=k;
else sum+=k;
}
if (ch[0]=='F') flag^=1;
if (ch[0]=='S')
{
x=get(); y=get();
Swap(x,y);
}
if (ch[0]=='P')
{
x=get(); y=get(); k=read();
if (flag) swap(x,y);
if (x<=y) Paint(1,x,y,k);
else
{
Paint(1,1,y,k);
Paint(1,x,n,k);
}
}
if (ch[0]=='C' && ch[1]=='S')
{
x=get(); y=get();
if (flag) swap(x,y);
if (x<=y) write(ask(1,x,y)),putchar(10);
else
{
int ans=ask(1,1,y)+ask(1,x,n);
if (tree[1].lval==tree[1].rval && ans!=1) ans--;
write(ans),putchar(10);
}
}
if (ch[0]=='C' && ch[1]!='S')
{
int ans=ask(1,1,n);
if (tree[1].lval==tree[1].rval && ans!=1) ans--;
write(ans),putchar(10);
}
}
return 0;
}