题目大意:
题目链接:https://jzoj.net/senior/#main/show/4248
求一个条边的多边形,相邻两边选择不同的颜色,共种颜色的涂色方案数。
思路:
以下解题思路时我在考试时一步一步的推理,希望直接了解方法的可以跳到“总结”处。
说明复杂度一定是级别的。(的拜拜)
先打一个表
| 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|
| 3 | 6 | 18 | 30 | 66 | 126 | 258 |
| 4 | 24 | 84 | 240 | 732 | 2184 | 6564 |
| 5 | 60 | 260 | 1020 | 4100 | 16380 | 65540 |
| 6 | 120 | 630 | 3120 | 15630 | 78120 | 390630 |
| 7 | 210 | 1302 | 7770 | 46662 | 279930 | 1679622 |
| 8 | 336 | 2408 | 16800 | 117656 | 823536 | 5764808 |
当时
显然发现它们都有公因数6,于是全部除以6
很容易发现如下规律
再来看的
明显都有6的公因数,提出来
还有一个因数2诶!
规律还是一样的!
第一次是6,第二次是12。
然后我就想到了小学奥数的列项。。。
然后一试,发现的最大公约数确实是20。
那么规律就出来了。
总结
然后。
所以很明显就是一个矩阵乘法。
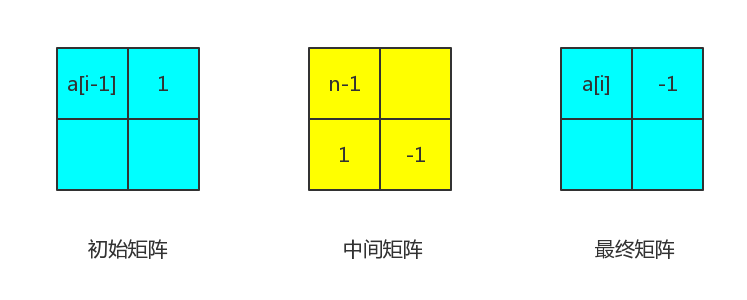
跑遍矩阵乘法就可以了。
代码:
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;
const ll MOD=1e9+7;
ll f[3][3],a[3][3],n,m;
void mul(ll f[3][3],ll a[3][3])
{
ll c[3][3]={{0,0,0},{0,0,0},{0,0,0}};
for (ll i=1;i<3;i++)
for (ll j=1;j<3;j++)
for (ll k=1;k<3;k++)
c[i][j]=(c[i][j]+f[i][k]*a[k][j]);
for (ll i=1;i<3;i++)
for (ll j=1;j<3;j++)
f[i][j]=c[i][j]%MOD;
}
void mulself(ll a[3][3])
{
ll c[3][3]={{0,0,0},{0,0,0},{0,0,0}};
for (ll i=1;i<3;i++)
for (ll j=1;j<3;j++)
for (ll k=1;k<3;k++)
c[i][j]=(c[i][j]+a[i][k]*a[k][j]);
for (ll i=1;i<3;i++)
for (ll j=1;j<3;j++)
a[i][j]=c[i][j]%MOD;
}
int main()
{
cin>>m>>n;
m-=3;
a[1][1]=(n-1)%MOD; a[2][1]=1; a[2][2]=-1;
f[1][1]=(n-2)%MOD; f[1][2]=1;
while (m>0)
{
if (m&1) mul(f,a);
mulself(a);
m>>=1;
}
cout<<f[1][1]%MOD*((n-1)%MOD)%MOD*(n%MOD)%MOD;
return 0;
}