【HDU2586】How far away ？【LCA】

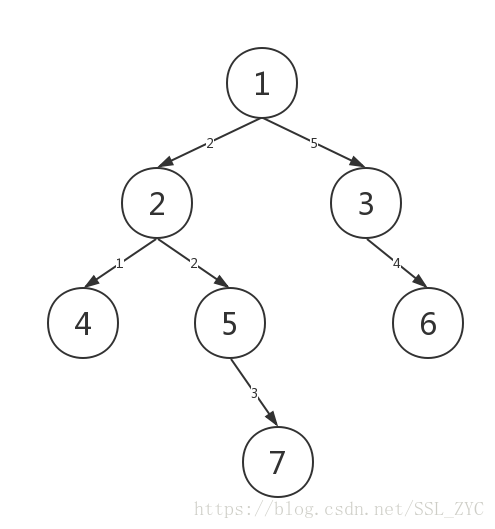
题目大意：

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2586
给出一棵树，每条边上有边权，求$x[i]$到$y[i]$的路径边权之和。

---

思路：

LCA模板题。
因为我们知道，任意两点$x$和$y$的距离=$x$到根的距离$+y$到根的距离$-2\times lca(x,y)$到根的距离。例如：

如果我们要求点$4$和点$7$的路径之和，我们可以先找到他们的$LCA$点$2$，然后就有
$dis[4][7]=dis[1][4]+dis[1][7]-2\times dis[1][2]$
为什么是这样呢？
首先我们把$dis[4][7]$分解成$dis[2][4]+dis[2][7]$。
$dis[1][4]=dis[2][4]+dis[1][2]$
$dis[1][7]=dis[2][7]+dis[1][2]$
那么$dis[1][4]+dis[1][7]=dis[2][4]+dis[2][7]+2\times dis[1][2]$
这正好比$dis[4][7]$多了$2\times dis[1][2]$
所以再减去$2\times dis[1][2]$即可。

那么同理，如果我们要求$x$到$y$的距离，我们先设他们的$LCA$为$lca$，这棵树的根节点为$root$，那么就有：
$dis[x][y]=dis[x][lca]+dis[y][lca]$
$dis[root][x]=dis[x][lca]+dis[root][lca]$
$dis[root][y]=dis[y][lca]+dis[root][lca]$
$dis[root][x]+dis[root][y]=dis[x][lca]+dis[y][lca]+2\times dis[root][lca]$
$dis[x][y]=dis[root][x]+dis[root][y]-2\times dis[root][lca]$
那么对于所有的$x[i]$和$y[i]$，我们就求出他们的$LCA$,然后按照公式输出即可。

---

代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 50100
#define LG 20
using namespace std;

int t,n,m,tot,f[N][LG],dep[N],head[N],dis[N];

struct edge
{
	int next,to,dis;
}e[N*2];

void add(int from,int to,int dis)
{
	e[++tot].to=to;
	e[tot].dis=dis;
	e[tot].next=head[from];
	head[from]=tot;
}

void dfs(int x,int fa,int k)  //预处理出f数组和任一点到root的距离
{
	dep[x]=dep[fa]+1;
	dis[x]=k;  //dis[x]表示点x到root的距离
	for (int i=1;i<=LG;i++)
	 f[x][i]=f[f[x][i-1]][i-1];
	for (int i=head[x];~i;i=e[i].next)
	 if (e[i].to!=fa)
	 {
	 	f[e[i].to][0]=x;
	 	dfs(e[i].to,x,k+e[i].dis);
	 }
}

int lca(int x,int y)
{
	if (dep[x]<dep[y]) swap(x,y);
	for (int i=LG;i>=0;i--)  //跳到同一高度
	 if (dep[f[x][i]]>=dep[y]) x=f[x][i];
	if (x==y) return x;
	for (int i=LG;i>=0;i--)  //继续跳
	 if (f[x][i]!=f[y][i])
	 {
	 	x=f[x][i];
	 	y=f[y][i];
	 }
	return f[x][0];
}

int main()
{
	scanf("%d",&t);
	while (t--)
	{
		memset(head,-1,sizeof(head));
		tot=0;
		scanf("%d%d",&n,&m);
		int x,y,z;
		for (int i=1;i<n;i++)
		{
			scanf("%d%d%d",&x,&y,&z);
			add(x,y,z);
			add(y,x,z);
		}
		dfs(1,0,0);
		for (int i=1;i<=m;i++)
		{
			scanf("%d%d",&x,&y);
			z=lca(x,y);
			printf("%d\n",dis[x]+dis[y]-dis[z]-dis[z]);
		}
	}
	return 0;
}