题目大意:
一个有向图,每条边有流量和费用,求在每个点只经过一次的情况下(和除外)的最小费用最大流。
思路:
原题也很容易看出是费用流。难点在于如何保证每个点只经过一次。
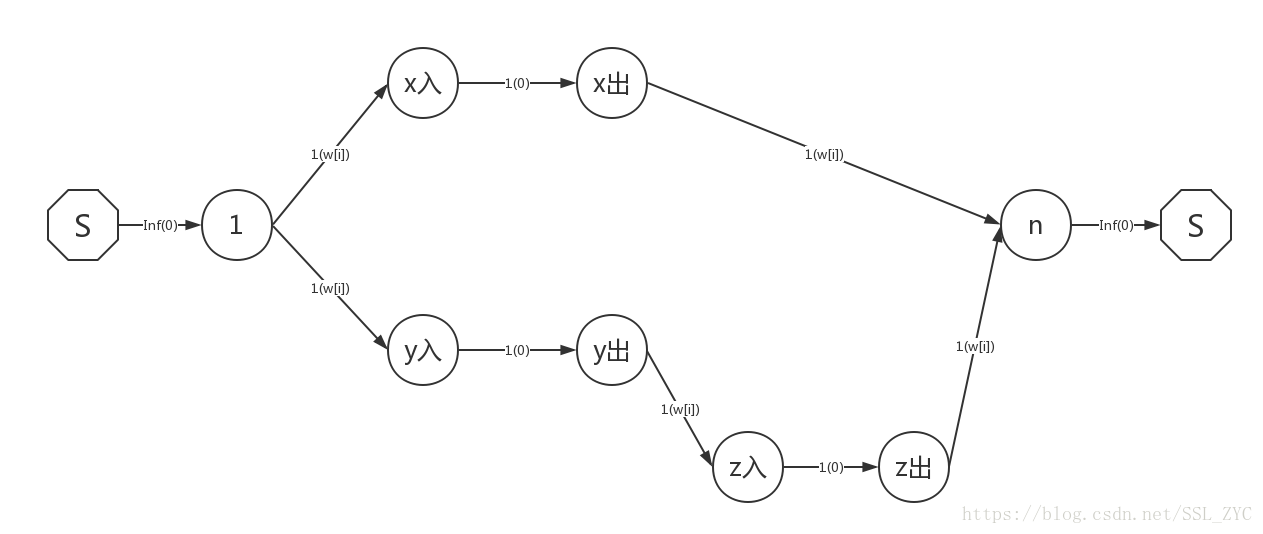
那么不妨将除之外的点进行拆点。每个点可以拆成入点和出点,流量为1,费用为0。这样就可以保证每个点之间的边只能走一次,就达成了每个点只能经过一次的效果。
最终的建模如下:
代码:
#include <cstdio>
#include <iostream>
#include <queue>
#include <cstring>
#define Inf 1e9
using namespace std;
int n,m,k,s,t,head[80001],dist[501],p[80001],x,y,z,minn,maxflow,cost;
bool vis[501];
struct edge
{
int next,c,to,w,from;
}e[80001];
void add(int from,int to,int c,int w)
{
k++;
e[k].from=from; //来的点
e[k].to=to;
e[k].c=c;
e[k].w=w;
e[k].next=head[from];
head[from]=k;
}
bool spfa()
{
for (int i=0;i<=2*n+3;i++)
{
dist[i]=Inf; //最短路
vis[i]=0;
}
queue<int> q;
q.push(s);
dist[s]=0;
vis[s]=1;
while (q.size())
{
int u=q.front();
q.pop();
vis[u]=0;
for (int i=head[u];~i;i=e[i].next)
{
if (!e[i].c) continue; //没流量了
int v=e[i].to;
if (dist[v]>dist[u]+e[i].w)
{
p[v]=i;
dist[v]=dist[u]+e[i].w;
if (!vis[v])
{
q.push(v);
vis[v]=1;
}
}
}
}
return (dist[t]<Inf);
}
void addflow()
{
minn=Inf+1;
for (int i=t;p[i];i=e[p[i]].from)
minn=min(minn,e[p[i]].c); //最小流量
for (int i=t;p[i];i=e[p[i]].from)
{
e[p[i]].c-=minn; //正向边
e[p[i]^1].c+=minn; //反向变
}
maxflow+=minn;
cost+=dist[t]*minn;
}
int main()
{
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
k=1;
s=n*2+1;
t=n*2+2;
add(s,n+1,Inf,0);
add(n+1,s,0,0);
add(n,t,Inf,0);
add(t,n,0,0);
for (int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x+n,y,1,z);
add(y,x+n,0,-z);
}
for (int i=2;i<n;i++)
{
add(i,i+n,1,0);
add(i+n,i,0,0);
}
while (spfa())
addflow();
printf("%d %d\n",maxflow,cost);
return 0;
}