49. 3种方法实现复杂链表的复制[clone of complex linked list]

【本文链接】

http://www.cnblogs.com/hellogiser/p/clone-of-complex-linked-list.html

【题目】

有一个复杂链表，其结点除了有一个next指针指向下一个结点外，还有一个sibling指向链表中的任一结点或者NULL。其结点的C++定义如下:

 C++ Code 

1 2 3 4 5 6 7

// complex node struct struct ComplexNode {     int value;     ComplexNode *next;     ComplexNode *sibling; };

 下图是一个含有5个结点的该类型复杂链表。图中实线箭头表示next指针，虚线箭头表示sibling指针。为简单起见，指向NULL的指针没有画出。

请完成函数ComplexNode* Clone(ComplexNode* pHead)，以复制一个复杂链表。

  【分析】

在常见的数据结构上稍加变化，这是一种很新颖的面试题。要在不到一个小时的时间里解决这种类型的题目，我们需要较快的反应能力，对数据结构透彻的理解以及扎实的编程功底。

分为2步：

（1）复制每一个节点，连接next，初步生成【新链表】，时间复杂度为T(n)=O(1)*n=O(n);

（2）连接sibling，假设在【新链表】中定位sibling的时间复杂度为T，则总的时间复杂度为T(n)=T*n;

由此可见，最为关键的是如何在【新链表】中快速定位sibling节点。

【方法1】

统计从头结点该sibling节点的步长step。

假设【原始链表】中的某节点N的sibling指向结点S。由于S的位置在链表上有可能在N的前面也可能在N的后面，所以要定位N的位置我们需要从原始链表的头结点开始找。假设从【原始链表】的头结点开始经过step步找到结点S。那么在【新链表】上从头结点开始经过step可以到结点N'的sibling对应的结点S'。定位sibling的时间复杂度为T=O(n) 。总的时间复杂度O(n²)，空间复杂度为O(1)。

【方法2】

使用map映射记录<A,A'>,<B,B'>,<C,C'>，这样定位sibling的时间复杂度为T=O(1) 。总的时间复杂度O(n)，但是空间复杂度为O(n)，相当与以O(n)的空间消耗实现了O(n)的时间效率。

【方法3】

根据原始链表的每个结点N，创建对应的N'。让后将N和N'连接起来，这样定位sibling的时间复杂度为T=O(1) ，之后重新分成2个链表即可。总的时间复杂度O(n)，空间复杂度为O(1)。

（1）创建新节点，并连接next。

（2）定位sibling并连接。

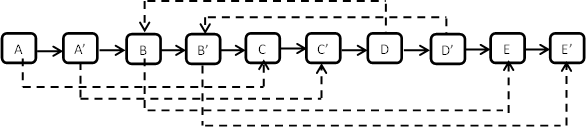
（3）链表拆分成两个：把奇数位置的结点链接起来就是原始链表，把偶数位置的结点链接出来就是复制出来的链表。

【代码】

 C++ Code 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89

// complex node struct struct ComplexNode {     int value;     ComplexNode *next;     ComplexNode *sibling; }; //Clone all nodes in a complex linked list with pHead, //and connect all nodes with next link. void CloneNodes(ComplexNode *pHead) {     //  A-A'-B-B'-C-C'     if(NULL == pHead)         return;     ComplexNode *pNode = pHead;     while(pNode != NULL)     {         ComplexNode *pNewNode = new ComplexNode();         pNewNode->value = pNode->value;         pNewNode->next = pNode->next;         pNewNode->sibling = NULL; // init NULL         // connect pNode and pNewNode         pNode->next = pNewNode;         //move to next node         pNode = pNewNode->next;     } } //Connect sibling nodes in a complex link list void ConnectSiblingNodes(ComplexNode *pHead) {     //  A-A'-B-B'-C-C'     if(NULL == pHead)         return;     ComplexNode *pNode = pHead;     while(pNode != NULL)     {         ComplexNode *pNewNode = pNode->next;         // connect sibling nodes         if(pNode->sibling != NULL)             pNewNode->sibling = pNode->sibling->next;         else             pNewNode->sibling = NULL;     } } // Split a complex list into two: // Reconnect nodes to get the original list, and its cloned list ComplexNode *ReconnectNodes(ComplexNode *pHead) {     //  A-A'-B-B'-C-C'     if(NULL == pHead)         return;     ComplexNode *pNode = pHead;     ComplexNode *pNewHead = pHead->next;     ComplexNode *pNewNode = pNewHead;     while(pNode != NULL)     {         // reconnect next nodes for pNode         pNode->next = pNewNode->next;         // move pNode to next         pNode = pNewNode->next;         // reconnect next nodes for pNewNode         if(pNode != NULL)         {             pNewNode->next = pNode->next;             pNewNode = pNode->next;         }         else         {             pNewNode->next = NULL;             pNewNode = NULL;         }     }     return pNewHead; } ComplexNode *Clone(ComplexNode *pHead) {     CloneNodes(pHead);     ConnectSiblingNodes(pHead);     return ReconnectNodes(pHead); }

【参考】

http://zhedahht.blog.163.com/blog/static/254111742010819104710337/

http://www.cnblogs.com/kedebug/archive/2012/12/21/2828131.html

【本文链接】

http://www.cnblogs.com/hellogiser/p/clone-of-complex-linked-list.html